Zwarte gaten (9): De firewall-paradox

Naast de informatieparadox zorgen zwarte gaten voor nog een paradox, die zo mogelijk nog controversiëler is. Als je in een zwart gat zou springen, zou je namelijk worden verbrand door een zinderend hete ‘muur van vuur’, iets wat volgens de algemene relativiteitstheorie van Einstein niet zou moeten kunnen. De paradox werd in 2012 ontdekt door de natuurkundigen Donald Marolf, Joe Polchinski en de natuurkundestudenten (!) Ahmed Almheiri en James Sully, en zorgt tot op de dag van vandaag voor grote verwarring en verhitte discussies tussen de beste natuurkundigen. Wie ook in de war is van deze paradox, bevindt zich dus in illuster gezelschap.

In dit artikel:

• De ingrediënten van de firewall-paradox
• De paradox
• Wat nu?

Afbeelding 1. Een zwart gat met een firewall.

Zoals we in dit artikel preciezer zullen uitleggen, is de paradox als volgt. Zwarte gaten kunnen verdampen, zoals Stephen Hawking liet zien, en ze vernietigen daarbij waarschijnlijk geen informatie. Dit behoud van informatie eist, dat een deeltje dat vrijkomt bij het verdampen ‘verstrengeld‘ moet zijn met deeltjes die eerder zijn vrijgekomen tijdens het verdampingsproces. Volgens de algemene relativiteitsteorie van Einstein daarentegen, is dit deeltje al verstrengeld met een deeltje in het zwarte gat. Deze ‘dubbele verstrengeling’ is onmogelijk vanwege de zogenaamde monogamie van verstrengeling. Als men dus aanneemt dat het zwarte gat inderdaad geen informatie vernietigt bij het verdampen, kan het deeltje dat vrijkomt bij het verdampen niet verstrengeld zijn met het deeltje binnenin. We zullen zien dat dit leidt tot een ‘muur van vuur’ (oftewel: ‘firewall’) om het zwarte gat heen.

Hoewel de meeste van de benodigde begrippen al eerder aan bod zijn gekomen in het dossier over zwarte gaten, zullen we deze in dit artikel eerst nog beknopt behandelen, zodat het in principe mogelijk is de paradox te begrijpen zonder de eerdere artikelen gelezen te hebben. Daarna kunnen we de paradox precies uitleggen, en zullen we ons tot slot afvragen hoe het nu verder moet met de natuurkunde…

De ingrediënten van de firewall-paradox

De firewall-paradox toont een tegenspraak tussen twee fundamenten van de theoretische natuurkunde: de tijdsomkeerbaarheid en het equivalentieprincipe uit de algemene relativiteitstheorie. Het eerste principe vormt een fundament van de theorie van het kleine: de quantummechanica, die beschrijft hoe de allerkleinste deeltjes zich gedragen. Het tweede principe vormt een fundament van de theorie van het grote: de algemene relativiteitstheorie, die beschrijft hoe planeten, sterren en zwarte gaten zich gedragen. Normaal gesproken staan deze theorieën op veilige afstand van elkaar omdat ze uitspraken doen over verschillende dingen (groot of klein), maar in de buurt van een zwart gat komen deze twee theorieën gevaarlijk dicht bij elkaar. Volgens de paradox kunnen ze dan namelijk onmogelijk allebei waar zijn! Dit terwijl het opgeven van een van de twee voor veel natuurkundigen niet tot de opties behoort.

Tijdsomkeerbaarheid en het equivalentieprincipe

Volgens de tijdsomkeerbaarheid is het altijd mogelijk om, als je alle natuurwetten en alle informatie over alle deeltjes zou kennen, vanuit elke gegeven situatie in het heden terug te rekenen naar de situatie in het verleden. Hieruit volgt direct dat informatie niet vernietigd kan worden. Zou dat namelijk wel kunnen, dan zouden er situaties zijn waarin we niet terug kunnen rekenen hoe het de situatie in het verleden was.

Het equivalentieprincipe zegt dat het in theorie onmogelijk is het verschil te merken tussen constant versneld zijn, en stilstaan ten opzichte van een bepaalde massa, zoals een planeet, ster of zwart gat. Om ervoor te zorgen dat je niet naar de massa toe valt zou je bijvoorbeeld een raket nodig hebben. Vanuit de raket gezien kun je niet weten of die massa er nu is, en je positie ten opzichte van die massa hetzelfde blijft, of dat er geen massa is, en je steeds sneller gaat. In het bijzonder betekent dit dat je, als je de raketmotor uitzet, niet kunt weten of je in vrije val bent of dat je je in de lege ruimte bevindt.

Het strijdtoneel, waarop een van deze twee geliefde principes zal moeten sneuvelen, is – hoe kan het ook anders – een zwart gat, en het wapen is verstrengeling.

Verstrengeling

Verstrengeling, waarover we ook al eerder hebben geschreven, heeft iets ‘magisch’. Het is een quantummechanisch effect, dat anders is dan al het andere waaraan je gewend bent in het dagelijks leven. Dit komt doordat de quantummechanica de theorie van het kleine is, en mensen zijn, vanuit deze theorie gezien, extreem groot.

Afbeelding 2. Verstrengeling.Als twee touwen met elkaar verstrengeld zijn, kunnen we vanuit de positie van het ene touw ook de positie van het andere bepalen. Als twee deeltjes met elkaar verstrengeld zijn is er ook een correlatie tussen hun eigenschappen: de eigenschappen van het ene deeltje bepalen de eigenschappen van het andere. Foto: William B. Folsom, NMFS.

In elke theorie, klassiek of quantummechanisch, kunnen deeltjes gecorreleerd zijn. Correlatie van deeltjes houdt in, dat als je iets weet over één deeltje, je ook iets weet over een tweede deeltje. Nu kunnen in de quantummechanica deeltjes gecorreleerd zijn op een manier die klassiek onmogelijk is. Deze deeltjes noemen we dan verstrengeld. We zullen deze twee manieren van correlatie uitleggen aan de hand van twee voorbeelden: eerst klassiek en dan quantummechanisch.

Alice en Bob spelen een spelletje. Het is een nogal saai spelletje, maar goed, ze mogen er wel voor naar een andere planeet. Ze hebben een vaas, met één zwart en één wit balletje. Blindelings pakken ze er allebei één. Alice gaat nu naar de maan en Bob blijft op aarde. Bob mag pas naar zijn balletje kijken als Alice op de maan is aangekomen. Zodra hij kijkt, en dus iets weet over de kleur van zijn balletje, weet hij onmiddellijk iets over de kleur van het balletje van Alice. (Die is natuurlijk van de kleur die Bob zelf niet heeft.) Dit betekent dat de kleur van de balletjes is gecorreleerd. Het is trouwens niet mogelijk om op deze manier sneller dan het licht informatie van de aarde naar de maan te sturen! Dit is omdat Bob niet kan bepalen wélk balletje hij krijgt.

Nu de quantummechanische variant van het spelletje. In plaats van balletjes hebben Alice en Bob nu deeltjes (bijvoorbeeld een elektron en zijn antideeltje, het positron), en in plaats van de kleuren wit en zwart hebben de deeltjes nu de eigenschappen ‘spin up’ (grofweg gezegd: linksom tollen) en ‘spin down’ (rechtsom tollen). Bovendien komen de deeltjes nu niet uit een vaas, maar uit een botsingsexperiment, zoals in het artikel over verstrengeling. Welke fysische eigenschappen van de deeltjes precies zijn gecorreleerd (spin up/spin down, wit/zwart) is trouwens niet zo belangrijk voor de paradox.

Ook nu neemt Alice haar deeltje mee naar de maan, en kijkt Bob op aarde naar zijn deeltje. Het enige belangrijke verschil met de klassieke variant, is dat de deeltjes van Bob en Alice zich, voordat Bob kijkt, tegelijk in de toestanden ‘Alice heeft spin up, Bob heeft spin down’ en ‘Alice heeft spin down en Bob heeft spin up’ kunnen bevinden. De deeltjes bevinden zich dan in een zogenaamde superpositie van die twee toestanden. Pas als Bob kijkt dwingt hij het deeltje, als het ware, een keuze te maken: spin up of spin down. Hij heeft, net als in het klassieke geval, 50% kans om één van beide te zien. Hij weet nu ook direct wat Alice heeft, namelijk het tegenovergestelde. Natuurlijk kan hiermee nog steeds geen informatie sneller dan het licht worden verzonden, omdat Bob nog steeds niet kan bepalen wat het resulaat van zijn meting zal zijn.

Het verschil tussen klassieke en quantummechanische correlatie is dus, dat klassiek gezien de balletjes zich altijd al in een van de twee toestanden bevonden, en quantummechanisch gezien de deeltjes pas echt hun eigenschappen aannemen als een ervan bekeken (of gemeten) wordt.

Verstrengeling is monogaam

Er is een aspect van van verstrengeling dat in voorgaande artikelen nog niet aan bod is gekomen. Een deeltje kan maar met één ander quantummechanisch systeem tegelijk verstrengeld zijn: verstrengeling is monogaam, net zoals dat mensen (althans in Nederland) maar met één iemand tegelijk getrouwd kunnen zijn.

Om dit uit te leggen beschouwen we weer het spelletje van Alice en Bob, maar nu is er een derde speler (en derde balletje): Charlie. Hij begint net als de anderen op aarde en krijgt ook één balletje. Alice gaat weer naar de maan, Bob blijft op aarde, en Charlie gaat naar Mars. Klassiek is er een (wederom nogal flauwe) strategie waarmee Bob op aarde, door naar zijn balletje te kijken, volledige informatie kan krijgen over het balletje van Alice én dat van Charlie. Deze strategie is eenvoudig. We beginnen met één balletje. Bob neemt dit balletje, wit of zwart, kopieert het tweemaal met een deeltjes-kopieerapparaat zonder zelf naar het balletje te kijken, en geeft de kopieën aan Alice en Charlie. Als Alice en Charlie op hun planeten zijn aangekomen, kijkt Bob naar zijn balletje. Hij weet nu natuurlijk direct wat de kleur is van de balletjes van Alice en Charlie.

Nu gaan we naar de quantummechanische variant van het spelletje met de drie spelers. Die is zoals het klassieke spelletje, maar dan weer met deeltjes (die in een superpositie kunnen zijn) in plaats van balletjes. Zoals we in een vorig artikel gezien hebben, is het kopiëren van quantumtoestanden echter lang niet zo eenvoudig als het kopiëren van ‘klassieke’ toestanden: er bestaat zelfs het zogeheten ‘no-cloning theorem‘. Dit leidt uiteindelijk tot wat we de ‘monogamie van verstrengeling’ noemen. Die monogamie van verstrengeling houdt in, dat als de drie deeltjes onderling verstrengeld zijn, er geen enkele strategie bestaat, waardoor Bob door het kijken naar zijn deeltje precies te weten kan komen wat voor een deeltje Alice heeft én wat voor een deeltje Charlie heeft. Met één van de deeltjes is het deeltje van Bob dus helemaal niet gecorreleerd (verstrengeld). Kortom: (het deeltje van) Bob kan niet tegelijk met (het deeltje van) Alice én met (het deeltje van) Charlie verstrengeld zijn. We zullen zien dat precies hierdoor de firewall-paradox ontstaat.

Afbeelding 3. Joe Polchinski, een van de bedenkers van de firewall-paradox.

Zwarte gaten

Zwarte gaten ontstaan als je ontzettend veel massa in een klein volume perst. Massa trekt massa aan middels de zwaartekracht. Deze onderlinge aantrekkingskracht kan dan zó groot worden, dat alle massa ineenstort tot een enkel punt. Er is een gebied om dit punt, waar de zwaartekracht nu zo sterk is dat er uit dit gebied werkelijk niets meer kan ontsnappen, zelfs geen licht. De grens tussen het gebied waarvandaan licht niet meer kan ontsnappen, en het gebied daarbuiten waar dat nog wel kan, heet de horizon. De horizon is géén materieel object, maar slechts de denkbeeldige grens tussen deze twee gebieden. Zoals we hierboven hebben gezien in het stukje over het equivalentieprincipe, merkt een waarnemer geen verschil tussen in vrije val zijn en in de lege ruimte zijn. Zo’n waarnemer merkt er zelf in eerste instantie dus ook niets van als hij of zij in een zwart gat valt en voorbij de horizon komt. Dat is ook logisch: er is daar namelijk helemaal niets!

Hawkingdeeltjes

De lege ruimte is quantummechanisch gezien, voor iedereen, niet écht helemaal leeg; het krioelt van de deeltjes en antideeltjes. Deze ontstaan paarsgewijs en heffen elkaar meestal snel weer op doordat ze weer bij elkaar komen. Zoals we hebben gezien, is er voor een persoon die in een zwart gat springt niets anders dan dit vacuüm. Echter, voor een waarnemer die boven de horizon zweeft, is de horizon wel een speciale plek. Achter deze grens ziet hij niets meer: de ruimte wordt als het ware in tweeën gekliefd. Als een deeltje en antideeltje worden gevormd in de buurt van de horizon, kan het gebeuren dat het antideeltje in het zwarte gat valt, maar het deeltje ontsnapt. Het deeltje dat ontsnapt is dan een zogenaamd Hawkingdeeltje. Het gevolg van het ontsnappen van deze deeltjes, is dat het zwarte gat verdampt.

Bovenstaande beschrijving is enigszins incompleet – er blijkt bijvoorbeeld niet heel duidelijk uit waarom juist de deeltjes uit een zwart gat kunnen ontsnappen, en de antideeltjes erin zouden vallen. Een betere beschrijving van Hawkingdeeltjes is in termen van het Unruh-effect, zoals in het eerder verschenen artikel over Hawkingstraling. Voor het begrijpen van de firewall-paradox echter, volstaat een grove beschrijving in termen van deeltjes en antideeltjes. Hawkingstraling en Hawkingdeeltjes zijn overigens min of meer hetzelfde; de Hawkingdeeltjes zijn de energiepakketjes (de ‘quanta‘) van de Hawkingstraling.

Naar boven

De paradox

Een recept des doods

De firewall-paradox ontstaat als we bedenken wat het verdampen van een zwart gat betekent voor de verstrengeling van Hawkingdeeltjes. We zullen zien dat het zwarte gat wel ‘oud’ genoeg moet zijn. Voor de duidelijkheid zullen we een antideeltje dat dan in het zwarte gat valt A noemen. Het Hawkingdeeltje dat daarbij hoort en ontsnapt, noemen we B. Alle Hawkingdeeltjes die in een eerder stadium zijn ontsnapt noemen we C.

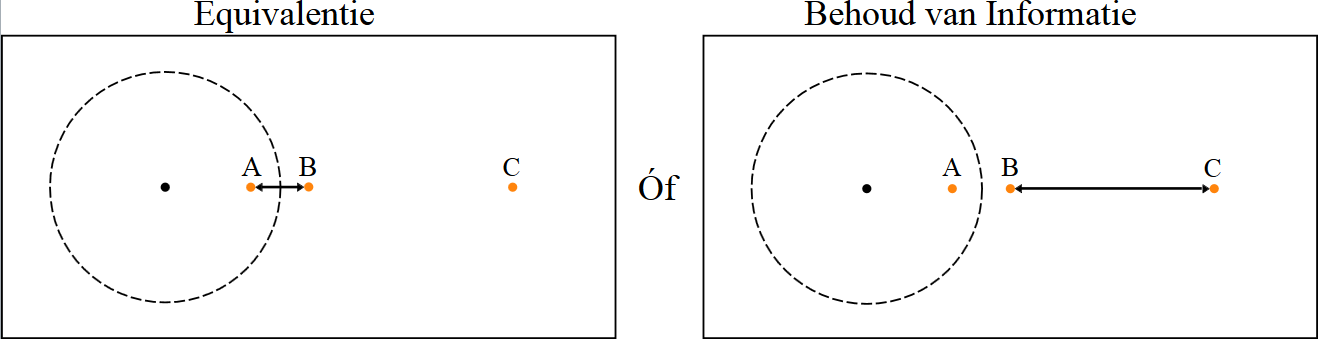
Afbeelding 4. De firewall-paradox.De stippellijn stelt de horizon van een zwart gat voor. Het equivalentieprincipe eist dat A met B is verstrengeld. Het behoud van Informatie eist dat B met C is verstrengeld. Vanwege de monogamie van verstrengeling kan kan dit niet allebei zo zijn.

We beschouwen nu de ervaringen van de drie spelers waar we al kennis mee hebben gemaakt: Alice, Bob en Charlie. Ditmaal springt Alice in het zwarte gat, en is dus in de buurt van deeltje A. Bob blijft vlak boven de horizon van het zwarte gat. Dit is bijvoorbeeld mogelijk met behulp van een raket, of een of andere constructie waarin hij aan een touwtje hangt. Bob is in de buurt van deeltje B. Tot slot hebben we Charlie, misschien wel de verstandigste van allemaal. Hij blijft ver weg van het zwarte gat, in de buurt van deeltjes C.

Hoe ervaart Charlie het ontstaan en het verdampen van het zwarte gat? Vóór de vorming van het zwarte gat ziet hij alleen maar materie. De materie stort later ineen en vormt een zwart gat. Veel later, als het zwarte gat al helemaal is verdampt, zijn er alleen nog maar Hawkingdeeltjes. Vanwege de tijdsomkeerbaarheid (oftewel het behoud van informatie) moet alle informatie over de materie die het zwarte gat vormde, aanwezig zijn in de Hawkingdeeltjes die uiteindelijk overblijven. In het algemeen zal het zwarte gat deze informatie helemaal door elkaar gehusseld hebben en is de informatie uitgesmeerd over alle deeltjes. De informatie over de materie die het zwarte gat vormde ligt nu niet meer voorhet oprapen: hij zit verstopt in de manier waarop de Hawkingdeeltjes met elkaar gecorreleerd – oftewel verstrengeld – zijn.

Aan een paar deeltjes heeft Charlie dus bijna niets qua informatie. Om echt iets te weten te komen over de materie die ooit het zwarte gat vormde, moet hij heel veel Hawkingdeeltjes hebben en uitzoeken hoe deze met elkaar gecorreleerd zijn. Dit lukt alleen als hij verhoudingsgewijs veel van de Hawkingdeeltjes heeft. (Om alles te weten te komen, moet hij zelfs alle Hawkingdeeltjes hebben.) Dus, als het zwarte gat nog ‘jong’ is, en er nog niet zo veel Hawkingdeeltjes zijn ontsnapt, dan bevatten deze Hawkingdeeltjes samen bijna geen informatie over de materie die het zwarte gat vormde. Als we daarentegen lang genoeg wachten tot we alle Hawkingdeeltjes waar kunnen nemen, hebben we alle informatie. Kortom: een Hawkingdeeltje dat ontsnapt wanneer het zwarte gat oud genoeg is (B), moet informatie met zich meedragen. Dat doet het Hawkingdeeltje door de manier waarop het verstrengeld is met eerder uitgezonden Hawkingdeeltjes (C). Dus, als een zwart gat geen informatie vernietigt, dan moet B verstrengeld zijn met C.

Dan nu Alice en Bob. Hoe zat het ook al weer met de Hawkingdeeltjes bij de horizon? Ziet iemand die in een zwart gat springt (Alice) deze deeltjes echt niet, zoals het equivalentieprincipe eist, hoewel iemand die buiten het zwarte gat blijft (Bob) deze deeltjes wel ziet? Het antwoord is: ja. Dit lijkt misschien raar, maar het wordt mogelijk gemaakt door iets anders ‘raars’, namelijk verstrengeling.

Het blijkt zo te zijn, dat de deeltjes en antideeltjes die worden gevormd in de lege ruimte tijdens hun kortstondige leven zijn verstrengeld. Dit kun je je misschien wel voorstellen omdat ze samen worden gevormd, en ze dus ‘bij elkaar horen’. In het geval dat een van deze deeltjes ontsnapt, en het andere in het zwarte gat verdwijnt, hebben we een Hawkingdeeltje buiten het zwarte gat. Hoewel dit deeltje ontsnapt (B), is het nog altijd verstrengeld met zijn ‘partner’ achter de horizon (A). Het blijkt zo te zijn, dat juist deze verstrengeling van A en B ervoor zorgt dat Alice inderdaad geen deeltjes ziet! Hoe deze verstrengeling precies werkt en waarom dat ervoor zorgt dat Alice geen deeltjes ziet, gaat iets te ver voor dit artikel. Om de paradox te kunnen begrijpen, is het alleen belangrijk te weten dat A en B op een speciale manier verstrengeld moeten zijn, en dat deze verstrengeling ervoor zorgt dat Alice geen deeltjes ziet, zoals het equivalentieprincipe eist. Kortom: volgens het equivalentiepricipe is A verstrengeld met B.

De paradox is – misschien voelde je hem al aankomen – dat vanwege de monogamie van verstrengeling, B niet met A én met C verstrengeld kan zijn. In andere woorden: of A en B zijn verstrengeld, of B en C zijn verstrengeld. Er zijn nu twee dingen die we zouden kunnen doen. Ten eerste zouden we kunnen aannemen, dat het equivalentieprincipe juist. A en B moeten dan verstrengeld zijn, anders zou Alice namelijk deeltjes bij de horizon tegenkomen. Daardoor kunnen B en C niet verstrengeld zijn. Aangezien deze verstrengeling noodzakelijk is voor het behoud van informatie, volgt dat informatie verloren gaat, wat in tegenspraak is met de tijdsomkeerbaarheid.

Ten tweede zouden we kunnen aannemen dat zwarte gaten geen informatie vernietigen. Dat betekent dat B en C verstrengeld zijn. Daardoor kunnen  A en B onmogelijk verstrengeld zijn. Juist deze verstrengeling zorgde ervoor, dat Alice bij de horizon geen deeltjes waarnam. Ze neemt nu dus wel deeltjes waar. Je kan uitrekenen dat deze deeltjes meer en meer energie hebben naarmate je dichter bij de horizon komt. (Bij de horizon zelf hebben ze zelfs oneindig veel energie.) Alles wat in een zwart gat valt wordt daarmee verbrand door een ‘muur van vuur’ nabij de horizon. Dit is de door Alice (en natuurkundigen) gevreesde ‘firewall’, waaraan de paradox zijn naam ontleent.

Afbeelding 5. Een firewall.Wanneer de deeltjes buiten de horizon niet met die binnen de horizon verstrengeld zijn, kan Alice deze deeltjes waarnemen. Ze vormen voor haar een hete ‘muur van vuur’: een firewall.

Naar boven

Wat nu?

We hebben gezien dat door de monogamie van de verstrengeling het equivalentiepincipe en tijdsomkeerbaarheid niet allebei waar kunnen zijn. Dit terwijl elke natuurkundige deze twee principes hoog in het vaandel heeft staan. De eerste reactie op de paradox, was dan ook dat de bedenkers ervan ergens een denkfoutje gemaakt moesten hebben. We zijn nu drie jaar verder, en er zijn inderdaad mensen die menen een fout te hebben gevonden. Hier is dan weer lang niet iedereen het mee eens… De paradox blijft dus een vruchtbare voedingsbodem voor discussie en verwarring.

Het mooie is, dat de firewall-paradox daarmee ook een voedingsbodem voor nieuwe natuurkunde vormt: als er inderdaad geen foutjes zitten in de redenering die tot de paradox leidt, is er een ware revolutie nodig om de paradox op te lossen. Een revolutie waarin de theorie van het grote en de theorie van het kleine vervangen worden door één theorie. Deze theorie van het grote én het kleine wordt ook wel de theorie van alles (’the theory of everything’) genoemd, al is die naam natuurlijk niet erg bescheiden. Snaartheorie is hiervoor een goede kandidaat, maar die theorie is nog lang niet helemaal uitgewerkt. Het is nog niet eens duidelijk of de snaartheorie wel echt de natuur beschrijft. De oplossing van de paradox zal dus nog even op zich laten wachten. Het spannende is, dat de oplossing ons een stapje dichterbij de volledige natuurkundige beschrijving van het universum zal brengen, en wie zit daar nou niet op te wachten?

Naar boven

Het tiende artikel in dit dossier behandelt de entropie van zwarte gaten.