Zwarte gaten (7): De informatieparadox (II)

In dit artikel:

• Verstrengeling
• Fundamentele kansen en kansen door onwetendheid
• De informatieparadox revisited

Afbeelding 1. De informatieparadox.Gaat informatie die in een zwart gat valt verloren, of bestaat er een manier om die informatie alsnog te achterhalen?

Verstrengeling

Om het begrip complementariteit te kunnen begrijpen, moeten we nog iets beter begrijpen wat ‘informatie’ op quantumniveau nu precies inhoudt. Een heel nuttig begrip daarbij is verstrengeling – een begrip dat we in het dossier over quantumfysica al uitgebreid tegenkwamen.

In de quantumfysica hoeft een natuurkundig systeem niet in één specifieke toestand te zijn. Een systeem kan ook in een zogeheten superpositie van toestanden zijn. Het bekendste voorbeeld is een elektron, waarvan de spin (grofweg de ‘hoeveelheid rondtollen’) twee basiswaarden kan aannemen, die we ‘spin up’ en ‘spin down’ noemen. Wie nog nooit van spin gehoord heeft, kan zich een elektron eenvoudigweg voorstellen als een computerbit. Zo’n bit kan ook twee waarden aannemen, die we bijvoorbeeld de getallen ‘0’ en ‘1’ kunnen laten voorstellen.

Het bijzondere van de quantummechanica is nu dat een elektron ook een beetje in de spin-uptoestand en een beetje in de spin-downtoestand kan zijn. In termen van de computerbit: een quantumbit (of qubit) kan deels in de toestand ‘0’ en deels in de toestand ‘1’ zijn. In hoeverre de qubit in elk van die toestanden is, geven we weer met een kans. We kunnen bijvoorbeeld een qubit maken die voor 30% in de toestand ‘0’ en voor 70% in de toestand ‘1’ is. Als we de toestand van heel veel van dergelijke qubits meten, worden deze waardes omgezet in echte kansen: in 30% van de gevallen zullen we dan een ‘0’ uitlezen, en in 70% van de gevallen een ‘1’.

Echt interessant wordt het als we nu in een botsingsexperiment elektronen en hun antideeltjes (positronen) in paren laten ontstaan. Het blijkt dat zo’n paar in de eenvoudigste experimenten altijd totale spin 0 heeft en dus netto niet rondtolt. Met andere woorden: als een elektron spin up heeft, heeft het tegelijk gevormde positron spin down, en andersom. Maar zoals gezegd: het elektron hoeft niet exact spin up of spin down the hebben – het kan ook voor 30% spin down en voor 70% spin up hebben. In dat geval heeft het bijbehorende positron voor 70% spin up en voor 30% spin down.

Dat betekent echter niet dat we die waarden nu kunnen zien als onafhankelijke kansen! Als we de spin van het elektron meten, zullen we in 30% van de gevallen spin down vinden, maar als we eenmaal die spin down gemeten hebben, weten we voor 100% zeker dat we voor het positron spin up zullen vinden. Met andere woorden: de twee deeltjes zijn verstrengeld: elk afzonderlijk hebben ze een bepaalde kans om in elk van de toestanden te zijn, maar zodra we van een van de deeltjes de toestand hebben gemeten, weten we onmiddellijk in welke toestand het andere deeltje is.

Afbeelding 2. Verstrengeling.Als twee touwen met elkaar verstrengeld zijn, bevinden ze zich noodzakelijkerwijs op dezelfde plaats. Als iemand ons vertelt waar het ene touw zich bevindt, weten we onmiddellijk ook de plaats van het andere touw. Precies hetzelfde geldt voor verstrengelde deeltjesparen: zodra we de spintoestand van één deeltje meten, weten we onmiddellijk ook de spintoestand van het andere deeltje. Foto: William B. Folsom, NMFS.

De bovenstaande beschrijving van verstrengeling is erg beknopt. Voor het begrijpen van dit artikel zou de uitleg hierboven voldoende moeten zijn, maar wie een veel beter idee wil krijgen van verstrengeling kan het aparte artikel daarover lezen, of zelf eraan rekenen in de lesmodule ‘Rekenen met Elektronen’ over quantumcomputers.

Naar boven

Fundamentele kansen en kansen door onwetendheid

Wat heeft dit alles nu met informatie en de informatieparadox te maken? Om dat te begrijpen moeten we nog één belangrijk begrip invoeren: het verschil tussen een fundamentele kans en een kans die gebaseerd is op onwetendheid. Ook dit begrip is in een eerder dossier uitgebreid besproken, dus ook hier volstaan we weer met een korte samenvatting.

De meeste kansen in ons dagelijks leven ontstaan door onwetendheid. De uitspraak “de kans om met een munt kop te gooien is 50% ” is daar een voorbeeld van. Als we aan het begin van de worp precies zouden weten wat de oriëntatie van de munt is, met welke snelheid hij gegooid wordt, wat de luchtstromingen zijn, hoe het profiel van de munt eruit ziet, enzovoort, zouden we in theorie met 100% zekerheid kunnen uitrekenen op welke zijde de munt terecht zou komen. Doordat we al die dingen niet exact weten, moeten we echter met een kansbegrip werken: als we het experiment herhalen met veel grofweg dezelfde maar op microscopisch niveau verschillende beginvoorwaarden valt de munt in 50% van de gevallen met ‘kop’ boven, en in 50% van de gevallen met ‘munt’. Dit is een voorbeeld van een kansproces dat ontstaat door onwetendheid.

Quantumkansen zijn echter een heel ander soort kansen. In het geval van een superpositie van quantumtoestanden – bijvoorbeeld een elektron dat voor 30% spin up en voor 70% spin down heeft – is er geen sprake van onwetendheid. Het elektron is echt op het meest fundamentele niveau in beide toestanden tegelijk. Het verschil tussen een dergelijke fundamentele kans en een kans door onwetendheid is in het voorbeeld van een elektron misschien moeilijk te zien, maar het verschil wordt duidelijker als we kijken naar bijvoorbeeld een lichtdeeltje (een foton) dat door twee spleten kan gaan. Zoals in dit artikel is uitgelegd, kan het interferentiepatroon dat dan op een scherm achter de twee spleten verschijnt, alleen verklaard worden door aan te nemen dat het foton daadwerkelijk door beide spleten tegelijk gaat.

Het belangrijkste verschil tussen deze twee kansbegrippen zit hem daarmee precies in het begrip informatie. Als een elektron in een superpositie van toestanden is, en we kennen de bijbehorende kansen, hebben we alle mogelijke informatie die de natuur ons kan geven. We weten weliswaar niet welke uitkomst voor de spin we bij een meting zullen vinden, maar de natuur zelf weet dit zogezegd ook niet: zolang er geen meting wordt gedaan, is de uitkomst fundamenteel onbepaald. In die zin hebben we dus volledige informatie over het quantumsysteem. In het voorbeeld van de munt is er juist een gebrek aan informatie.

Afbeelding 3. Kansen en informatie.Wanneer we met een dobbelsteen gooien, is de kans op elk van de mogelijke uitkomsten 1 op 6. Dit kansbegrip ontstaat door onwetendheid: we hebben niet voldoende informatie over de beginsituatie van de worp om de uitkomst te bepalen. Quantumkansen daarentegen zijn fundamenteel: zelfs als we volledige informatie over een quantumsysteem hebben, zijn er in het algemeen nog verschillende uitkomsten van een meting mogelijk, met verschillende bijbehorende kansen. Foto: Wikipedia-gebruiker Diacritica.

Verwarrend? Het verschil tussen deze twee vormen van ‘kans’ is, zeker voor wie er voor het eerst mee in aanraking komt, begripsmatig inderdaad erg lastig. Lees bovenstaande alinea’s dus gerust twee, drie of tien keer, om het verschil goed te begrijpen. Of voor wie van meer variatie houdt: lees het artikel over quantumkansen in het dossier over quantumfysica, of maak de lesmodule over de EPR-paradox.

Naar boven

De informatieparadox revisited

Gewapend met alle bovenstaande kennis kunnen we nu de informatieparadox veel nauwkeuriger in quantumtaal beschrijven. Stel dat we beginnen met het experiment dat we hierboven al besproken hebben: we laten een elektron en een positron als paar ontstaan in een botsing van andere deeltjes. Zoals gezegd is de totale spin van de ontstane deeltjes in dit geval nul. Bovendien zal het in eenvoudige experimenten zo zijn dat geen van beide deeltjes een ‘voorkeursrichting’ heeft. De toestand waarin het deeltjespaar ontstaat zal dus de volgende superpositie zijn: voor 50% is het paar in de toestand ‘elektron spin up; positron spin down’, en voor 50% in de toestand ‘elektron spin down; positron spin up’. Zoals hierboven uitgelegd: dit is een superpositie, dus ondanks dat we de uitkomst van een meting niet weten, hebben we in dit geval volledige informatie over het systeem.

Nu wordt het hoog tijd om een zwart gat in het verhaal te brengen. We vinden ergens een zwart gat (in praktijk natuurlijk iets dat niet meevalt en de nodige gevaren met zich meebrengt, maar in een gedachte-experiment geen enkel probleem), en we laten het positron in dit zwarte gat vallen terwijl we het elektron op veilige afstand erbuiten houden. Is er daarmee iets aan ons systeem veranderd?

In eerste instantie lijkt dat niet het geval, maar als we iets beter over deze situatie nadenken, zien we dat er toch een probleem is ontstaan. Er is namelijk geen enkele manier waarop we te weten kunnen komen wat er in het zwarte gat gebeurt: er kan immers geen licht of andere vorm van straling of materie aan het zwarte gat ontsnappen. Ook de Hawkingstraling helpt ons hier niet: Hawking liet immers zien dat die straling ons niets anders vertelt dan wat de temperatuur en dus de massa van het zwarte gat is – dus zeker niets over gedetailleerde processen die zich al dan niet in het zwarte gat afspelen. Het zou prima kunnen dat iets of iemand in het zwarte gat meet wat de toestand van het positron is, maar we zullen daar  nooit achter komen. Voor de waarnemer buiten het zwarte gat bestaat daarmee in zekere zin alleen het elektron nog, en de vraag of het elektron nu spin up of spin down heeft is opeens een kwestie van onwetendheid geworden! Het zwarte gat heeft door het verwijderen van alle kennis over de helft van het systeem een fundamentele kans omgezet in een kans door onwetendheid. Kortom: er is informatie verloren gegaan ondanks dat dit in een quantumtheorie eigenlijk niet zou moeten kunnen – de informatieparadox.

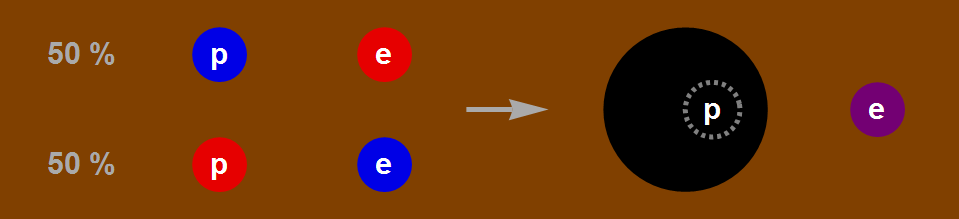
Afbeelding 4. Een grafische weergave van de informatieparadox.Links een deeltjespaar bestaande uit een positron (p) en een elektron (e). Het paar is in een superpositie van toestanden: het is voor 50% in de toestand “positron spin up (blauw), elektron spin down (rood)”, en voor 50% in de tegengestelde toestand. Deze gegevens vormen samen de volledige informatie over het quantumsysteem. Rechts is het positron in een zwart gat verdwenen. Daarmee hebben we geen volledige informatie meer over het systeem: de spin van het positron zou binnenin het zwarte gat gemeten kunnen worden, maar we kunnen dat buiten het zwarte gat nooit ontdekken. In dit geval is er nog altijd een kans van 50% op elk van de mogelijke meetuitkomsten voor de spin van het elektron (aangegeven door de paarse kleur – het “gemiddelde” van rood en blauw), maar deze kansen zijn nu een gevolg van onze onwetendheid.

Bovenstaande beschrijving van de informatieparadox is weliswaar moeilijker te begrijpen dan een beschrijving in termen van stoelen en televisies, maar deze beschrijving ligt wel veel dichter bij de beschrijving die Hawking oorspronkelijk gaf. Bovendien maakt deze formulering heel goed duidelijk waar de mogelijke oplossing gezocht moet worden: als we op de een of andere manier de kennis over het ‘verdwenen’ positron toch weer terug kunnen krijgen uit het zwarte gat, hebben we weer volledige informatie over het systeem, en gaat er dus geen informatie verloren.

Zoals we in het vorige artikel zagen is dat – het toch behouden blijven van de informatie – de oplossing die lijkt te volgen uit de AdS/CFT-correspondentie van Juan Maldacena. De ‘million dollar question’ voor de theoretische natuurkunde is dus: hoe kunnen we de informatie over het tweede deeltje weer van achter de horizon van het zwarte gat tevoorschijn toveren? Of is het misschien zelfs zo dat die informatie nooit achter de horizon verdwijnt? Het antwoord weten we niet met 100% zekerheid, maar er bestaan allerlei interessante ideeën over. In de komende artikelen willen we enkele van deze ideeën bespreken, te beginnen met een idee dat tot voor kort misschien wel het meest populaire was: complementariteit. In het daarop volgende artikel zullen we vervolgens zien waarom een recente ontdekking natuurkundigen toch weer aan dit idee van complementariteit heeft doen twijfelen, en welke nieuwe suggesties dit idee zouden kunnen vervangen.

Naar boven

In het achtste artikel in deze serie, beschrijven we het begrip complementariteit, en vragen we ons af of dat idee een oplossing van de informatieparadox kan zijn.

Afbeelding blokkenschema: Wikipedia-gebruiker Alain r.