Zwarte gaten (2): De horizon

In dit artikel:

• Ontsnappingssnelheid: een formule
• De Schwarzschildstraal
• Kun je ontsnappen aan een zwart gat?

Afbeelding 1. Een zwart gat zuigt de materie van een nabije ster op.Ontsnappen aan een zwart gat is niet eenvoudig. In dit artikel zullen we zien dat er zelfs een “point of no return” bestaat, waarvandaan ontsnappen onmogelijk lijkt! Afbeelding: NASA.

Ontsnappingsnelheid: een formule

Zoals we in het vorige artikel hebben gezien, heeft elke planeet, ster of andere opeenhoping van materie een ontsnappingssnelheid: een minimumsnelheid waarmee je van dat object af moet bewegen om zonder verdere hulp aan de zwaartekracht te kunnen ontsnappen. Vanaf het aardoppervlak is die ontsnappingssnelheid bijvoorbeeld zo’n 11,2 kilometer per seconde.

Waar hangt de grootte van de ontsnappingssnelheid precies van af? Om te beginnen natuurlijk van de hoeveelheid materie die voor de aantrekking zorgt: de massa van de ster of planeet. Maar de ontsnappingssnelheid hangt ook af van de plaats waar we ons bevinden. Vanaf het aardoppervlak moeten we met 11,2 km/s omhoog bewegen om zonder hulp aan de zwaartekracht te ontsnappen, maar als we ons op tienduizenden kilometers boven het aardoppervlak zouden bevinden, is de zwaartekracht veel zwakker, en hoeven we dus ook minder snel te bewegen.

Het blijkt dat we deze eigenschappen van het begrip ontsnappingssnelheid in een betrekkelijk eenvoudige formule kunnen uitdrukken. De ontsnappingssnelheid v_ont is uit te rekenen als

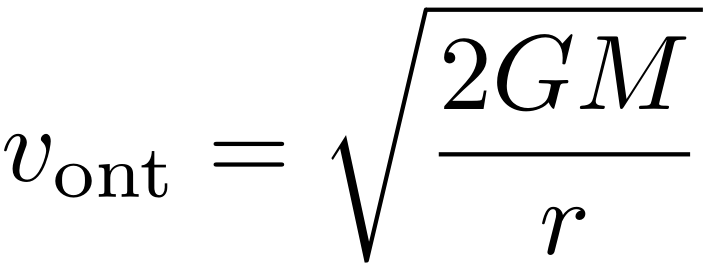
We zien in deze formule duidelijk wat hierboven in woorden werd gezegd: de ontsnappingssnelheid hangt af van de massa, M, van de planeet of ster, en van de afstand, r. Let op: die afstand wordt gemeten tot het middelpunt van de massa (dus in ons voorbeeld: het middelpunt van de aarde), niet tot het oppervlak! Het symbool G, ten slotte, is de zwaartekrachtsconstante van Newton, een natuurconstante die ongeveer gelijk is aan 6,67 × 10^-11 m³ kg^-1 s^-2.

Wie van rekenen houdt, kan in deze formule de massa van de aarde (5,97 × 10²⁴ kg) en onze afstand tot het centrum van de aarde (6,37 × 10⁶ m) invullen, en zal vinden dat de ontsnappingssnelheid op het aardoppervlak inderdaad ongeveer 11,2 km/s is.

Naar boven

De Schwarzschildstraal

In het vorige artikel zagen we dat een zwart gat ontstaat als licht niet meer aan een zwaar object kan ontsnappen. In dat geval moet de ontsnappingssnelheid dus gelijk zijn aan de lichtsnelheid, zo’n 300.000 kilometer per seconde (oftewel 3,00 × 10⁸ m/s). We geven deze snelheid vaak aan met het symbool c. Uit de formule in het vorige hoofdstukje zien we dat er twee manieren zijn om de ontsnappingssnelheid zo hoog te maken: we moeten ofwel een heel zwaar object creëren (dan wordt de massa M heel groot), of we moeten zorgen dat een bepaalde hoeveelheid massa zich in een heel klein gebied bevindt, zodat we de afstand r tot het centrum van die massa heel klein kunnen maken.

Afbeelding 2. Karl Schwarzschild (1873-1916).

Dat laatste is misschien een onverwacht resultaat: elke hoeveelheid materie kan dus een zwart gat worden, als we die materie maar in een klein genoeg gebied weten te persen! Wie handig is met formules kan de berekening zelf doen: kies de ontsnappingssnelheid in de eerder gegeven formule gelijk aan de lichtsnelheid, c, en reken de bijbehorende straal r uit. Dit sommetje geeft het volgende antwoord:

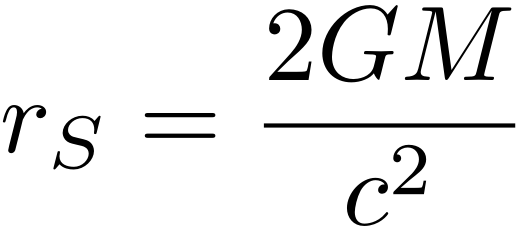
We hebben deze speciale afstand r_S genoemd, waarbij de S staat voor de achternaam van de Duitser Karl Schwardzschild (1873-1916), een natuurkundige die we in het volgende artikel in deze serie nog uitgebreider zullen tegenkomen. De Schwardzschildstraal r_S is dus de straal van het bolletje waarin we een bepaalde massa M moeten proppen om van die massa een zwart gat te maken. Enthousiaste rekenaars kunnen weer proberen dit voor de aarde uit te rekenen, en zullen vinden dat de aarde een zwart gat wordt als we haar in een bolletje met een straal van ongeveer 9mm weten te proppen. Geen eenvoudige opgave, natuurlijk!

Natuurlijk zouden we de aarde (in theorie) ook kleiner dan dat kunnen maken. Dan is de ontsnappingssnelheid op het denkbeeldige aardoppervlak nog hoger dan de lichtsnelheid. De aarde is dan dus een nog krachtiger zwart gat. Ook in dat geval kan licht tot aan een afstand van 9 mm van het centrum van deze micro-aarde niet ontsnappen. Hoe klein we de micro-aarde ook maken, die afstand van 9 mm blijft hetzelfde. Met andere woorden: zodra de aarde een zwart gat wordt, heeft het mini-planeetje altijd een denkbeeldige “schil” om zich heen op een afstand die gelijk is aan de Scwardzschildstraal. Van binnen deze schil zal licht niet kunnen ontsnappen; daarbuiten kan het dat wel.

Deze denkbeeldige schil wordt ook wel de horizon van het zwarte genoemd. Net als bij het gewone begrip horizon kunnen we van buitenaf niet verder kijken dan die grens, omdat licht die grens niet kan passeren. Voor elke massa kunnen we de grootte van die horizon uitrekenen: die is gelijk aan de Schwardzschildstraal.

Afbeelding 3. De horizon.Net als het aardoppervlak heeft ook een zwart gat een horizon: een denkbeeldige grens van waarachter geen licht naar ons toe kan komen. Foto: Marcus Dall Col.

Naar boven

Kun je ontsnappen aan een zwart gat?

Tot nu toe hebben we het alleen maar gehad over licht dat niet aan een zwart gat kan ontsnappen. Echt interessant wordt het natuurlijk als we bedenken dat Einstein in zijn relativiteitstheorie liet zien dat niets sneller kan bewegen dan het licht. Hoe veel energie we ook in een raket of een ander voorwerp pompen, de snelheid zal nooit groter worden dan de beroemde 300.000 km/s. (Wie veel meer hierover wil lezen kan daarvoor terecht in ons dossier over relativiteitstheorie.) De vraag ligt dus voor de hand: betekent dat dat er helemaal niets aan een zwart gat kan ontsnappen?

In eerste instantie lijkt die conclusie misschien wat voorbarig. Zo hebben we in het voorgaande steeds gezegd dat de onstnappingssnelheid de snelheid is waarmee je zonder hulp aan een zwaartekrachtsveld kunt ontsnappen. Die toevoeging is belangrijk: als we bijvoorbeeld kijken naar de snelheid waarmee raketten gelanceerd worden, bereikt deze snelheid nooit de 11,2 km/s. (Het snelheidsrecord met de Ariane-raket is bijvoorbeeld 10,4 km/s.) Dat hoeft ook helemaal niet: de raket begint op te stijgen met een lagere snelheid dan 11,2 km/s, maar blijft met behulp van zijn motoren versnellen terwijl hij van de aarde af beweegt. Op grotere hoogten is de afstand r tot het middelpunt van de aarde groter geworden, en hoeft de raket dus een minder grote snelheid te bereiken om te kunnen ontsnappen.

Kunnen we dus niet op een soortgelijke manier aan een zwart gat ontsnappen? Of, misschien nog eenvoudiger: kunnen we op een zwart gat niet eerst een heel hoge toren bouwen, tot op een hoogte waar de ontsnappingssnelheid lager is dan de lichtsnelheid, en dan vanaf die toren aan het zwarte gat ontsnappen?

Het antwoord op deze vragen is: nee, dat kan niet. Om te begrijpen waarom niet zullen we onze “klassieke” beschrijving van zwarte gaten moeten verlaten, en moeten kijken naar de manier waarop deze objecten in de relativiteitstheorie beschreven worden. Dat is dan ook het onderwerp van het volgende artikel in deze serie.

Naar boven

In het derde artikel van het dossier over zwarte gaten bespreken we de relativistische eigenschappen van zwarte gaten.