Bijna-extreme zwarte gaten

Eerst even een korte opfrisser: wat zijn extreme zwarte gaten ook alweer? Zwarte gaten worden beschreven aan de hand van drie eigenschappen: de massa \( M \), de lading \(Q\) en de draaiing \(J\). Deze eigenschappen zijn niet helemaal onafhankelijk van elkaar, want bij een bepaalde lading en draaiing (gemeten in slimme eenheden) komt een minimale massa die het zwarte gat moet hebben:

\( M \geq \sqrt{J^2 + Q^2}. \)

Als de massa kleiner is dan bovenstaande waarde, verdwijnt de waarnemingshorizon van het zwarte gat en spreken we van een naakte singulariteit. Natuurkundigen verwachten dat zulke objecten niet voorkomen in de natuur, en dus zeggen we dat de massa van het zwarte gat niet onder de extreme waarde van \( \sqrt{J^2 + Q^2}\) kan komen. Zwarte gaten met exact die massa worden dan ook extreme zwarte gaten genoemd.

Het vorige artikel ging over het feit dat lang gedacht werd dat er geen natuurlijk proces is dat zo’n extreem zwart gat kan vormen, maar dat er recentelijk getwijfeld wordt aan die aanname. Waar niet over getwijfeld wordt, is dat bijna-extreme zwarte gaten kunnen bestaan: zwarte gaten die een massa hebben nét boven de extreme limiet.  Ook deze bijna-extreme zwarte gaten hebben veel bijzondere eigenschappen. De belangrijkste is misschien wel het feit dat dichtbij de horizon een extra symmetrie lijkt te ontstaan waar natuurkundigen veel aan hebben.

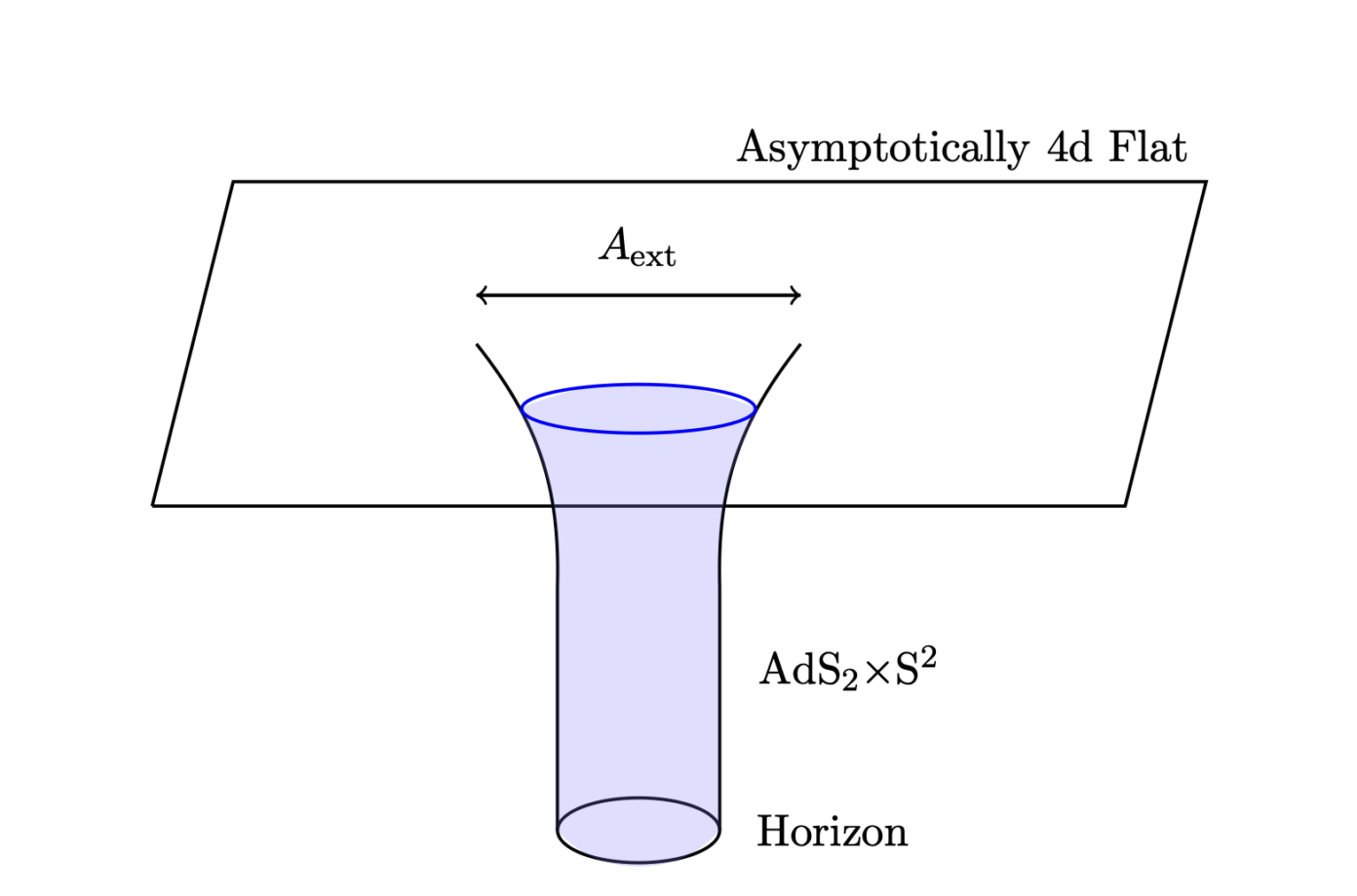
Elk zwart gat heeft, zoals ik in het vorige artikel beschreef, niet één maar eigenlijk twee horizonnen: een ‘binnenste’ en een ‘buitenste’. Voor extreme zwarte gaten vallen de binnenste en buitenste horizonnen samen op dezelfde straal: \(r_\pm = r_H\).  Bij bijna-extreme zwarte gaten is er een heel klein verschil tussen deze twee stralen: \(r_\pm = r_H \pm \epsilon \), waarbij \(\epsilon\) een heel kleine afstand is. Als we nu inzoomen op de (buitenste) horizon van zo’n bijna-extreem zwart gat, gebeurt er iets heel bijzonders. De ruimtetijd rondom de horizon van het zwarte gat lijkt heel veel op de Anti-de-Sitterruimte, die regelmatige lezers ongetwijfeld herkennen uit de veelbesproken AdS/CFT-correspondentie! Voor die gelijkenis maakt het niet uit in welke ruimtetijd het oorspronkelijke zwarte gat zich bevond: voor elke kosmologische constante (positief, negatief, nul) en voor elk aantal dimensies gebeurt dit. De ruimtetijd die ontstaat lijkt op een tweedimensionale AdS-ruimte gecombineerd met een andere ruimtetijd. Hoewel die andere ruimtetijd wél anders is voor verschillende bijna-extreme zwarte gaten, is de tweedimensionale AdS-ruimte universeel.

Theoretisch natuurkundigen willen zwarte gaten heel graag beter begrijpen. Zwarte gaten leveren namelijk veel vragen op, zoals de informatieparadox. De informatieparadox is een vraagstuk dat opkomt bij het combineren van de algemene relativiteitstheorie van Einstein, die de zwaartekracht van objecten met grote massa’s beschrijft, en de quantumtheorie, die objecten op hele kleine schaal beschrijft. Zeker bij zwarte gaten, waar veel massa op een kleine afstand samenkomt, is een theorie die beide werelden met elkaar verenigt belangrijk. De manier waarop we dat vaak doen levert de informatieparadox op: we begrijpen niet goed wat er dan gebeurt met de informatie die deeltjes die het zwarte gat in vallen met zich meedragen. Voor het begrijpen van zwarte gaten als quantumsystemen is het belangrijk om de ruimtetijd goed te kunnen splitsen in een gebied dat we beschrijven als het zwarte gat, en een gebied dat we ‘de rest’ noemen. Voor ‘gewone’ zwarte gaten is dit nogal lastig. Een quantumsysteem kun je, om technische redenen die te ver gaan om hier uit te leggen, niet opsplitsen in een gebied binnen de waarnemingshorizon en een gebied buiten de waarnemingshorizon. Maar in het geval van een bijna-extreem zwart gat kun je de ruimte wél opknippen in het AdS-achtige gebied en het deel daarbuiten. Dit is de opzet die gebruikt werd in onderzoeken die een belangrijke stap hebben gezet in het oplossen van de informatieparadox.

Waar extreme zwarte gaten een temperatuur van nul hebben, hebben bijna-extreme zwarte gaten een heel lage Hawkingtemperatuur. Dit betekent dat, hoewel ze wel verdampen, waardoor de informatieparadox een rol speelt, ze dit slechts heel langzaam doen. Dit geeft ook meer controle over het rekenwerk aan zo’n zwarte gat, aangezien het betekent dat het maar langzaam verandert van eigenschappen en dit maakt het bestuderen van het zwarte gat door middel van gedachte-experimenten makkelijker.

De quantumveldentheorie die de omgeving van het zwarte gat in deze limiet beschrijft, heeft ook nog een bijzondere universele eigenschap. De materie die voorkomt in deze theorie is afhankelijk van de oorspronkelijke theorie vóór het inzoomen, en van de exacte eigenschappen van het zwarte gat. Bij alle varianten bevat de actie, een object dat de tijdsevolutie van het systeem bepaalt, ook een specifieke term die Jackiw-Teitelboim-zwaartekracht, kortweg JT-zwaartekracht, wordt genoemd.  Om deze reden zijn theoretisch natuurkundigen dol op het bestuderen van JT-zwaartekracht in tweedimensionale Anti-de-Sitterruimte. Zo bij elkaar lijken die woorden heel willekeurig en specifiek gekozen, zeker omdat ons eigen universum geen Anti-de-Sitterruimte is – en al helemaal niet tweedimensionaal! Maar zoals je ziet kan deze exotische theorie toch gebruikt worden in ons universum, heel dicht bij de horizon van bijna-extreme zwarte gaten.

Bijna-extreme zwarte gaten vormen dus een perfect speelveld voor theoretisch natuurkundigen. Aan de ene kant kan er gerekend worden aan de wildste theorieën, waarbij een van de favoriete tools van de moderne theoretisch natuurkundigen – de AdS/CFT-correspondentie – van pas komt, en aan de andere kant worden bijna-extreme zwarte gaten daadwerkelijk verwacht in ons universum!

QU is sinds kort weer actief op Instagram! Volg ons voor nieuws en aankondigingen van nieuwe artikelen: https://www.instagram.com/quantumuniverse.nl/