Zwarte gaten (5): De informatieparadox

In dit artikel:

• De temperatuur van een zwart gat
• Zwarte stralers
• Tijdsomkeerbaarheid
• De informatieparadox
• Een weddenschap

Afbeelding 1. De informatieparadox.Wat gebeurt er met informatie die in een zwart gat valt?

De temperatuur van een zwart gat

Steek een ijzeren staaf in het vuur, en de staaf zal gaan gloeien. Warm ijzer straalt dus licht uit. Wat we vaak niet beseffen, is dat dit geldt bij elke temperatuur: ook als de staaf nog lang niet zo warm is dat hij “roodgloeiend” is, straalt het ijzer al licht uit. Dat licht heeft echter een veel langere golflengte dan zichtbaar licht, waardoor we het met het blote oog niet kunnen zien. Nachtkijkers werken op dit principe. Warme voorwerpen stralen infraroodstraling uit, die in zo’n kijker wordt omgezet in een zichtbaar beeld.

Kortom: elk voorwerp dat een temperatuur heeft boven het absolute nulpunt (grofweg -273 graden Celsius) straalt een bepaalde hoeveelheid straling uit, en die straling heeft een golflengte die van de temperatuur afhangt. Hoe hoger de temperatuur, hoe korter de golflengte van de uitgezonden straling.

Het omgekeerde geldt ook. Als voorwerpen straling uitzenden, kunnen we aan de hand van de golflengte van die straling de temperatuur van het voorwerp uitrekenen. Dat geldt in het bijzonder voor zwarte gaten. We hebben in het vorige artikel gezien hoe Stephen Hawking aantoonde dat zwarte gaten een kleine hoeveelheid straling moeten uitzenden. Aan de hand van de eigenschappen van die straling kan dus ook de temperatuur van het zwarte gat berekend worden. Hawking zelf gaf al een formule voor die temperatuur, T:

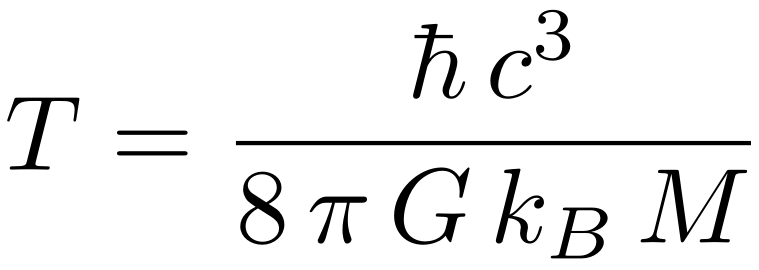
Die formule lijkt nogal ingewikkeld, maar dat komt met name omdat er allerlei constantes in staan. De constante ħ is de constante van Planck, c is de lichtsnelheid, π is het bekende getal 3,1415…, G is de zwaartekrachtsconstante van Newton, en k_B is de thermodynamische constante van Boltzmann. Al die constantes hebben een bekende waarde, dus we kunnen die waardes ook gewoon invullen. We vinden dan een veel eenvoudigere formule:

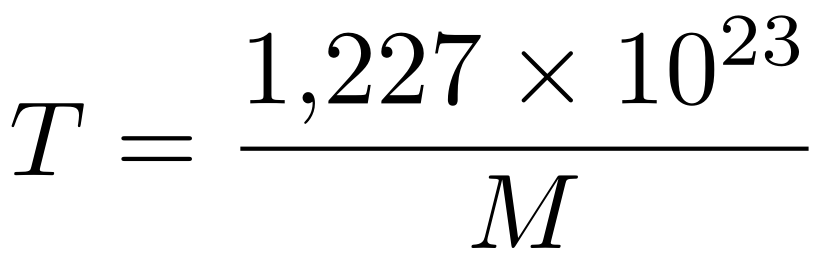
Hierin is M de massa (in kilogrammen) van het zwarte gat. Kortom: er is een heel eenvoudig verband tussen de hoeveelheid massa (de totale hoeveelheid materie) die in een zwart gat zit, en de temperatuur die het heeft.

De liefhebbers kunnen zelf uitrekenen wat de temperatuur van de Hawkingstraling zou zijn als we bijvoorbeeld onze zon (met een massa van 1,989 × 10³⁰ kg) zouden samenpersen tot een zwart gat. Die temperatuur is niet erg groot: de berekening komt uit op ongeveer 0,00000006 graden. Merk op dat dit graden boven het absolute nulpunt zijn, niet boven het vriespunt!

Een interessant gevolg hiervan is dat een zwart gat met eenzelfde massa als de zon in de praktijk helemaal niet zal verdampen. Het zwarte gat straalt weliswaar een heel klein beetje Hawkingstraling uit, maar het vangt intussen ook een heleboel straling op. Het heelal zelf is immers ook gevuld met allerlei straling, de bekende achtergrondstraling. De hoeveelheid straling die ons zonsmassa-zwarte gat opvangt, is vele malen groter dan de hoeveelheid straling die het uitzendt. Het zwarte gat blijft dus voorlopig nog groeien! Pas als over heel lange tijd het heelal zelf zo ver is afgekoeld dat het minder straling uitzendt dan een dergelijk zwart gat, zal het verdampingsproces daadwerkelijk beginnen.

Afbeelding 2. De Maan.Grote zwarte gaten zullen in het algemeen minder Hawkingstraling uitzenden dan ze achtergrondstraling opvangen. Alleen kleine zwarte gaten stralen zo veel Hawkingstraling uit dat ze daadwerkelijk verdampen. De grens ligt ongeveer bij een zwart gat met evenveel massa als de Maan. Foto: Gregory H. Revera.

Aan de formule voor de temperatuur hierboven kunnen we zien dat een kleiner zwart gat (met minder massa), een hogere temperatuur zal hebben. Er kunnen dus wel degelijk kleinere zwarte gaten bestaan die nu al verdampen. Om dat te laten gebeuren, moet de straling van het zwarte gat een hogere temperatuur hebben dan die van de achtergrondstraling. Die laatste temperatuur is gemeten, en is ongeveer 2,7 graden boven het absolute nulpunt. Wie de berekening weer doet, zal ontdekken dat een verdampend zwart gat op dit moment een massa moet hebben van ten hoogste 4,5 × 10²² kg – grofweg de massa van de Maan.

Naar boven

Zwarte stralers

We zeiden hierboven dat de temperatuur van een voorwerp vertaald wordt in de golflengte van de straling die het uitzendt. We moeten die uitspraak nog iets preciezer maken, want voorwerpen zenden zelden straling van maar één golflengte uit. Een betere uitspraak is: de temperatuur van een voorwerp wordt vertaald in de gemiddelde golflengte van de straling die het uitzendt.

Hoe de verdeling van de golflengtes van de uitgezonden straling rondom dat gemiddelde precies is, hangt af van allerlei eigenschappen van het voorwerp. Bijvoorbeeld: een voorwerp dat van zichzelf een rode kleur heeft, heeft de neiging om rood licht te weerkaatsen, maar blauw licht te absorberen. Die eigenschap vertaalt zich bij het opwarmen van het voorwerp in het feit dat blauw licht (met een korte golflengte) juist makkelijker wordt uitgezonden, en rood licht (met een lange golflengte) moeilijker.

De precieze verdeling van de golflengtes van het licht dat een warm voorwerp uitzendt, wordt het spectrum van dat voorwerp genoemd. Het precies berekenen van zo’n spectrum aan de hand van de eigenschappen van het voorwerp is heel lastig. Er is één uitzondering op die regel: als een voorwerp van zichzelf perfect zwart is, en dus geen enkele kleur licht reflecteert, kunnen we heel precies uitrekenen wat het spectrum van zo’n voorwerp is als we het opwarmen. Een dergelijk voorwerp wordt een zwart lichaam of een zwarte straler genoemd. Een opmerking terzijde: de straling van zwarte lichamen speelde ook in de ontdekking van de quantummechanica een cruciale rol!

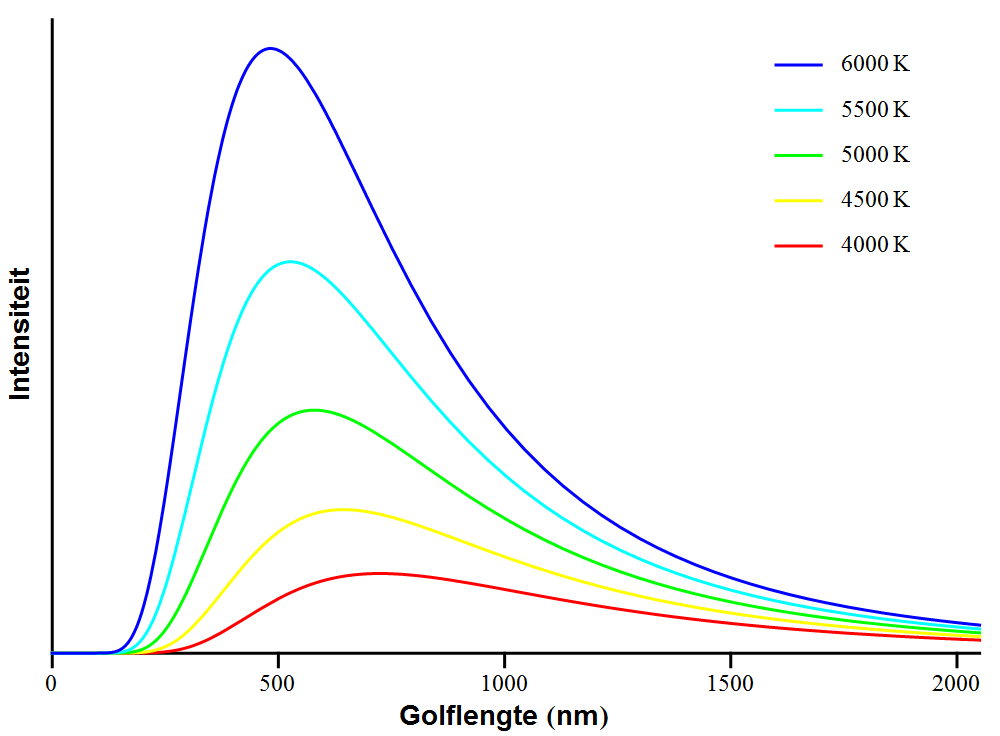
Afbeelding 3. Het spectrum van zwarte stralers.Voor zwarte lichamen van vijf verschillende temperaturen staat in deze grafiek uitgezet hoeveel straling ze van welke golflengte uitzenden. We zien dat warmere voorwerpen veel meer straling uitzenden, en dat die straling gemiddeld iets kortere golflengtes heeft dan bij minder warme voorwerpen.

In afbeelding 3 zien we een aantal spectra van zwarte stralers in een grafiek getekend. Twee dingen vallen op. Ten eerste: hoe warmer het zwarte lichaam wordt, hoe meer straling het zal uitzenden. Dit is een logische conclusie, die we hierboven ook al gebruikt hebben. Een zwart gat moet bijvoorbeeld warm genoeg zijn om zo veel straling te kunnen uitzenden dat de achtergrondstraling gecompenseerd wordt en het zwarte gat verdampt.

Het tweede dat opvalt is iets wat we ook al eerder noemden: de gemiddelde golflengte van de straling (dat wil zeggen: de golflengte van de piek van het spectrum) verandert als de temperatuur verandert. We zien in afbeelding 3 dat de piek langzaam naar links schuift als de temperatuur stijgt. Een warmer voorwerp zendt dus licht van (gemiddeld) kortere golflengtes uit. Deze eigenschap kunnen we zoals gezegd gebruiken om de situatie om te draaien, en uit de golflengte van een zwarte straler zijn temperatuur te berekenen.

Een heel belangrijke opmerking over de spectra die we in afbeelding 3 zien, is de volgende. De vorm van die spectra hangt voor zwarte stralers alleen af van de temperatuur. Met andere woorden: zodra we de temperatuur van de zwarte straler weten, weten we niet alleen waar de piek van het spectrum ligt, maar we weten ook precies hoeveel straling die straler voor een willekeurige golflengte zal uitzenden. Deze schijnbaar onschuldige opmerking blijkt voor zwarte gaten grote gevolgen te hebben!

Naar boven

Tijdsomkeerbaarheid

Om te kunnen begrijpen waarom de laatste opmerking voor zwarte gaten zo cruciaal is, moeten we eerst stilstaan bij een belangrijke eigenschap van de natuur. Die eigenschap is tijdsomkeerbaarheid: vrijwel alle fundamentele processen die we in de natuur om ons heen zien, zijn omkeerbaar in de tijd.

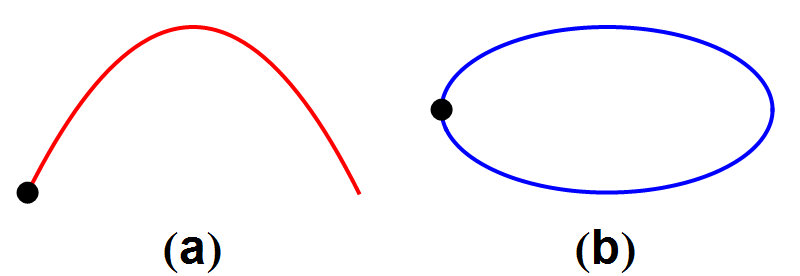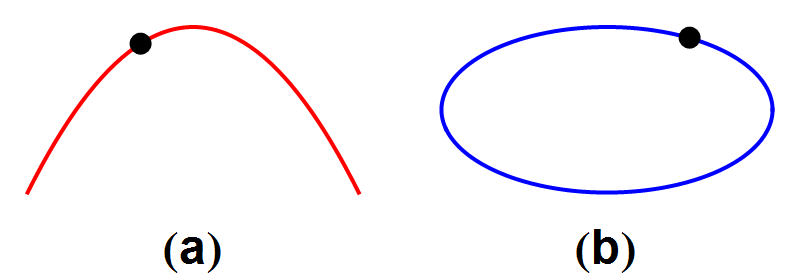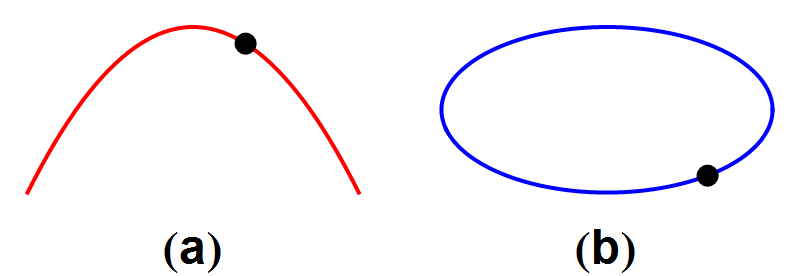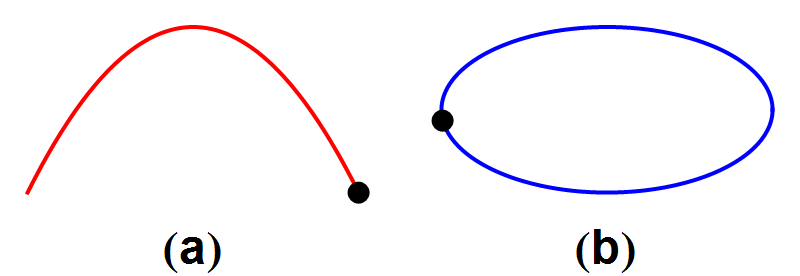
Afbeelding 4. Tijdsomkeerbaarheid van mechanische processen (I).Links zien we een paraboolbaan, zoals bijvoorbeeld een bal of kogel die aflegt. Rechts een elliptische baan zoals die bijvoorbeeld door hemellichamen die om de zon draaien wordt beschreven.

In afbeelding 4 zien we twee voorbeelden uit de mechanica: links een paraboolbaan die door bijvoorbeeld een weggeslagen golfbal wordt afgelegd; rechts een elliptische baan zoals die bijvoorbeeld door een komeet om de zon wordt beschreven. Voor allebei de processen geldt dat de tijdsomgekeerde baan ook in de natuur kan voorkomen: zie afbeelding 5.

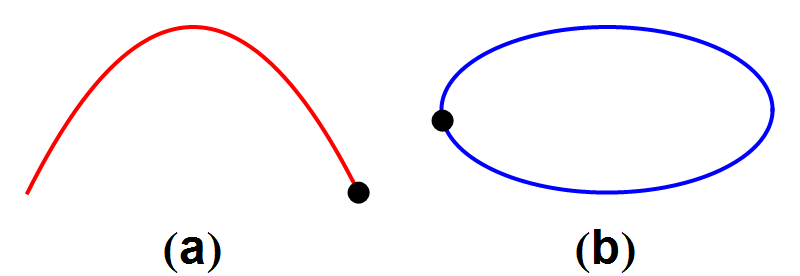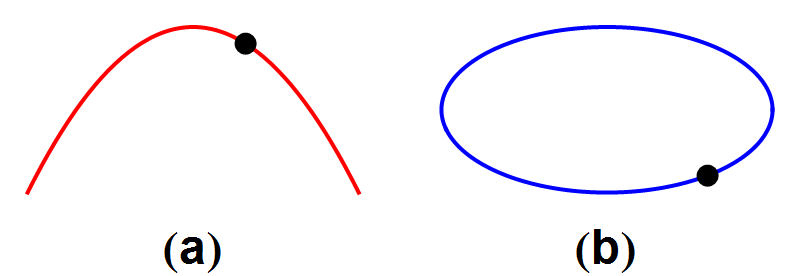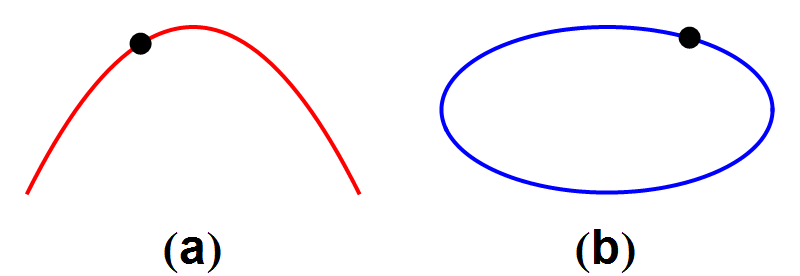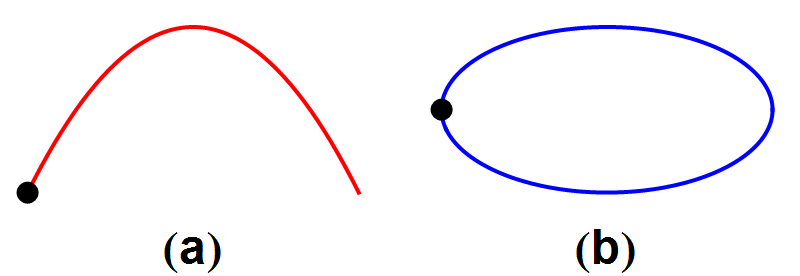
Afbeelding 5. Tijdsomkeerbaarheid van mechanische processen (II).De tijdsomgekeerde banen van afbeelding 4 beschrijven ook fysisch mogelijke processen.

Zijn deze voorbeelden niet te eenvoudig? In zekere zin wel: als we bijvoorbeeld een glas op de grond kapot laten vallen, zien we een proces waarvan we het tijdsomgekeerde nooit zien. Hoe lang we ook wachten, de stukjes glas zullen nooit meer spontaan de lucht in vliegen en weer een glas vormen. De reden is echter niet dat dit proces onmogelijk is, maar dat het heel onwaarschijnlijk is. Als we elk glasscherfje, en zelfs elk molecuul daarin, en elk molecuul in de lucht, precies de omgekeerde snelheid zouden geven van de snelheid die het had op het moment dat de brokstukken op de grond kwamen, zouden we inderdaad voor onze ogen weer spontaan een glas zien ontstaan. De fundamentele processen zijn dus nog altijd tijdsomkeerbaar, ondanks dat de kans op dit exacte proces vanuit de eindproducten extreem klein is. Wie meer wil weten over tijdsomkeerbaarheid en kansprocessen kan daarover uitgebreid lezen in ons dossier over entropie.

De tijdsomkeerbaarheid van de fundamentele natuurwetten heeft een belangrijk gevolg: we kunnen uit de eindsituatie van een proces in principe altijd terugrekenen naar de beginsituatie. Als we een golfbal zien aankomen, kunnen we uitrekenen waar die vandaan kwam; als we een komeet waarnemen kunnen we ook uitrekenen waar deze komeet tweeduizend jaar geleden aan de hemel stond.

Alles wat we hier gezegd hebben geldt voor alle natuurwetten die tot op heden ontdekt zijn. Tijdsomkeerbaarheid en de mogelijkheid tot “terugrekenen” lijken dus fundamentele eigenschappen van de natuur te zijn. Die fundamentele eigenschappen gelden ook voor de wetten van de relativiteitstheorie en de quantummechanica. Om heel precies te zijn: in het geval van de quantummechanica zijn er wat kleine lettertjes. De wetten van de quantumfysica zijn op het allerkleinste niveau alleen tijdsomkeerbaar als we tegelijkertijd ook de ladingen van alle deeltjes omdraaien en het systeem dat we beschrijven spiegelen. Hoe dan ook, ook in dat geval geldt nog altijd dat we uit een eindsituatie altijd terug kunnen rekenen naar de beginsituatie.

Naar boven

De informatieparadox

Nu komen we echter tot een heel vreemde conclusie. Als zowel de relativiteitstheorie als de quantummechanica de mogelijkheid bieden om van een eindsituatie terug te rekenen naar een beginsituatie, zouden we verwachten dat dat voor de combinatie van die twee theorieën ook geldt. Hoe zit dat bijvoorbeeld voor zwarte gaten, waarin zoals we gezien hebben beide theorieën een belangrijke rol spelen?

Laten we een eenvoudig gedachte-experiment doen. We nemen twee precies dezelfde zwarte gaten, met een massa van bijvoorbeeld 1000 kg. (We nemen de massa relatief klein, zodat het zwarte gat kan verdampen.) Vervolgens laten we het ene zwarte gat een stoel van 5 kg opslokken, en het andere een televisie die ook precies 5 kg weegt. Beide zwarte gaten wegen nu 1005 kg. Vervolgens laten we de zwarte gaten helemaal verdampen, tot er niets meer van over is.

Kunnen we nu uit de twee eindsituaties terugrekenen naar de beginsituaties? Met andere woorden: kunnen we uiteindelijk achterhalen in welk zwart gat we de stoel hebben gegooid, en in welk de televisie? Van de zwarte gaten zelf is niets meer over, dus die informatie zullen we uit de uitgezonden straling moeten halen. Maar zoals we hierboven zagen, hangt de hoeveelheid en de golflengte van die straling alleen af van de massa van het zwarte gat. Kortom: we verwachten dat de twee zwarte gaten van 1005 kg op exact dezelfde manier verdampen, en daarbij exact dezelfde straling uitzenden!

Hiermee staan we voor een raadsel. Zowel de quantummechanica als de relativiteitstheorie zijn tijdsomkeerbaar. Toch blijkt de straling van zwarte gaten, die gebaseerd is op die twee theorieën, zo te zijn dat een eindsituatie (de Hawkingstraling) geen enkele informatie bevat over de beginsituatie (de voorwerpen die in het zwarte gat vielen). Deze schijnbare tegenspraak wordt de informatieparadox genoemd.

Naar boven

Een weddenschap

Afbeelding 6. John Preskill, Kip Thorne en Stephen Hawking.Hawking, Preskill en Thorne sloten in 1997 een beroemde weddenschap af over de informatieparadox. Foto: Caltech / Heidi Aspaturian.

Ook Hawking zelf zat met deze paradox in zijn maag. Er waren wat hem betreft drie mogelijke oplossingen:

1. Overblijfselen. Zwarte gaten zullen nooit helemaal verdampen: er blijft altijd een overblijfsel over, en dat overblijfsel bevat de informatie over wat er oorspronkelijk in het zwarte gat viel.
2. Informatieverlies. Er gaat in het verdampingsproces wel degelijk informatie verloren. Dat zou betekenen dat tijdsomkeerbaarheid toch niet zo’n fundamentele eigenschap van de natuur is als we dachten. Bovendien zou het betekenen dat ofwel de quantummechanica, ofwel de relativiteitstheorie (en mogelijk beide) op fundamenteel niveau niet helemaal juist is.
3. Informatiebehoud. Er gaat in het verdampingsproces geen informatie verloren; uiteindelijk is uit de straling toch af te leiden of we begonnen met een stoel of met een televisie. Dat zou betekenen dat Hawkings oorspronkelijke berekening niet helemaal juist was en dat Hawkingstraling zich niet helemaal gedraagt als de straling van een perfect zwarte straler.

Optie (1) lijkt de meest onwaarschijnlijke; er is niet direct een reden te bedenken waarom zwarte gaten overblijfselen zouden vertonen, en het lijkt heel lastig om in zulke (waarschijnlijk microscopisch kleine) overblijfselen enorme hoeveelheden informatie op te slaan. De meeste natuurkundigen vermoedden dus dat optie (2) of optie (3) het juiste antwoord zou blijken te zijn, maar welke van de twee dat dan was, was verre van duidelijk.

In 1997 leidde dit zelfs tot een beroemde weddenschap tussen Hawking en zijn collega’s Kip Thorne en John Preskill. Hawking zelf geloofde dat er niets mis zou blijken te zijn met zijn oorspronkelijke berekening, en dat een zwart gat dus inderdaad op een bepaalde manier informatie vernietigt – optie (2) hierboven. Kip Thorne was het met hem eens, maar John Preskill kon zich niet voorstellen dat tijdsomkeerbaarheid in de natuur geschonden zou zijn – hij wedde dus op optie (3). De materiële inzet van de weddenschap was niet heel groot: de winnaar of winnaars zouden een encyclopedie naar keuze krijgen. (Het waren de dagen voor het internet, dus bij het opslaan van grote hoeveelheden informatie dacht men nog aan encyclopedieën.) In termen van fundamentele kennis over de natuur was de inzet natuurlijk in zekere zin veel groter!

De informatieparadox houdt tot op de dag van vandaag de gemoederen van veel fysici bezig. We hebben sinds 1997 heel veel geleerd over of en hoe zwarte gaten informatie uitstralen – zo veel zelfs, dat de weddenschap tussen Hawking en zijn collega’s inmiddels door twee van de drie partijen beëindigd is. Welke partijen dat waren, wat het bijbehorende argument was, wie er won en waarom de derde van de drie nog altijd niet overtuigd is, bespreken we in het volgende artikel in dit dossier.

Naar boven

Het zesde artikel in deze serie gaat over holografie en de informatieparadox.