Zwarte gaten (10): Zwarte gaten en entropie

In dit artikel:

• De temperatuur van een zwart gat
• Entropie
• Heeft een zwart gat entropie?

Afbeelding 1. Temperatuur.Voorwerpen die straling uitzenden (zoals een warme oven) hebben daarmee ook een temperatuur. Ook zwarte gaten zenden straling uit – de beroemde Hawkingstraling – en ook van een zwart gat zouden we dus de temperatuur moeten kunnen bepalen. Foto: Wikipedia-gebruiker Gmhofmann.

De temperatuur van een zwart gat

Zoals we inmiddels uitgebreid hebben gezien, zijn zwarte gaten niet helemaal zwart. Ze stralen een heel kleine hoeveelheid Hawkingstraling uit. Een van de gevolgen daarvan is dat zwarte gaten, net als alle andere voorwerpen die straling uitzenden, een temperatuur hebben. In het artikel over Hawkingstraling zagen we al dat Stephen Hawking ook een precieze formule voor die temperatuur afleidde. Hij ontdekte dat de temperatuur van een zwart gat, T, gelijk moet zijn aan

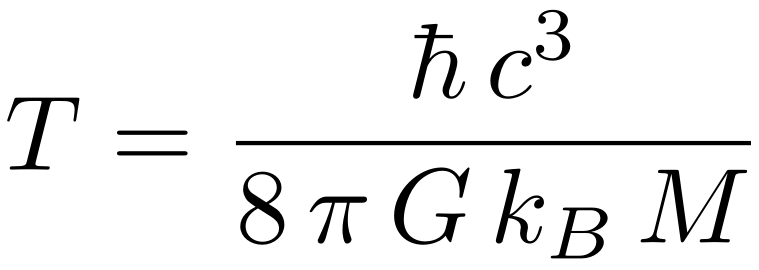
Deze formule ziet er op het eerste gezicht indrukwekkend uit, maar we kunnen haar vereenvoudigen door te bedenken dat bijna alle symbolen die erin voorkomen bekende natuurconstanten zijn. Zo is c de lichtsnelheid (3,0 × 10⁸ m/s), ħ de constante van Planck (1,1 × 10^-34 kg m² / s), G de zwaartekrachtsconstante van Newton (6,7 × 10^-11 m³ / kg s²) en k_B de thermodynamische constante van Boltzmann (1,4 × 10^-23 kg m² / s² K). Het getal π, ten slotte, is het beroemde getal dat de verhouding tussen de omtrek en de diameter van een cirkel bepaalt – ongeveer gelijk aan 3,14.

De enige onbepaalde natuurkundige grootheden die in de formule van Hawking voorkomen, zijn dus de temperatuur, T, en de massa, M, van het zwarte gat. Kortom: de temperatuur van een zwart gat wordt alleen bepaald door zijn massa. Om dit duidelijker in de formule tot uiting te laten komen, kunnen we twee dingen doen. Ten eerste kunnen we de getalswaarden van alle natuurconstanten invullen. Dat leidt tot de beduidend eenvoudigere formule

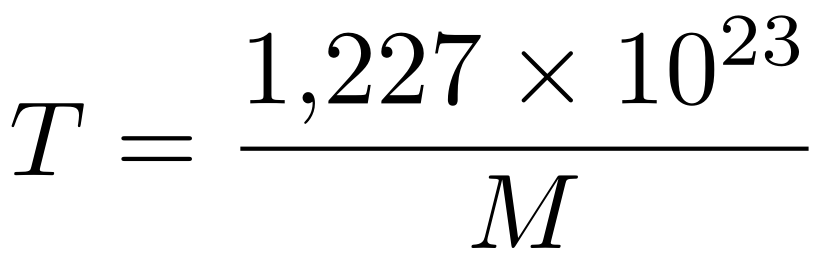
In deze formule kunnen we heel eenvoudig de massa M in kilogrammen invullen, en zo de temperatuur van een zwart gat uitrekenen.

Er is echter nog een andere manier om de temperatuurformule een veel eenvoudiger uiterlijk te geven. Laten we bijvoorbeeld eens kijken naar één natuurconstante die in die formule voorkomt: de lichtsnelheid c. Die constante is grofweg gelijk aan 300.000 kilometer per seconde. Als we afstanden meten in kilometers en tijden in secondes, moeten we in onze formule dus het getal 300.000 invullen. Maar we zouden ook kunnen besluiten om afstanden te meten in meters, in mijlen, in inches, enzovoort. In al die gevallen moeten we natuurlijk een andere getalswaarde voor c in de formule invullen, zodat c nog altijd de snelheid van het licht in de gekozen eenheden weergeeft. (Bovendien moeten we alle andere natuurconstantes in de formule ook omrekenen naar deze nieuw gekozen eenheden.)

De eenvoudigste keuze die we kunnen maken is het meten van afstanden in lichtsecondes – de afstand die het licht in één seconde aflegt. Eén zo’n lichtseconde is 300.000 kilometer lang, en het licht legt in één seconde dus – per definitie – één lichtseconde af. Met andere woorden: de getalswaarde van c in deze eenheden is eenvoudigweg 1. Het mooie is nu dat we deze procedure kunnen voortzetten: we kunnen ook voor massa, tijdsduur en temperatuur slimmere eenheden kiezen, zodat de getalswaarden van alle constanten, c, ħ, G en k_B, gelijk wordt aan 1. (Als we deze keuze maken voor c, ħ en G heten de resulterende eenheden overigens de Planckeenheden – zie het artikel daarover voor veel meer informatie.) Ook in termen van deze speciale eenheden wordt de formule van Hawking dus veel eenvoudiger: die ziet er dan uit als

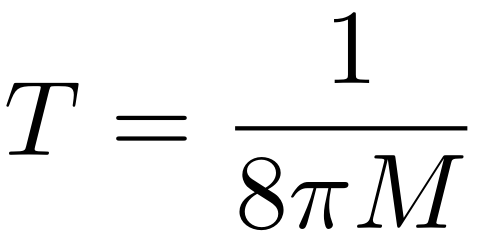
Alleen de getallen 8 en π komen nog in deze formule voor, en we zien weer direct dat de temperatuur T van een zwart gat alleen van zijn massa M afhangt. Natuurkundigen houden van eenvoudige formules waarin zo weinig mogelijk ingewikkelde natuurconstantes voorkomen, en dit is dan ook de vorm waarin de formule van Hawking het meest gebruikt wordt. We zullen deze vorm in het volgende artikel weer tegenkomen.

Een opmerking terzijde: dankzij Einsteins beroemde formule E=mc² weten we dat energie en massa twee verschijningsvormen van dezelfde natuurkundige grootheid zijn. Merk nu op dat in de formule van Hawking de massa, M, van het zwarte gat onder de deelstreep staat. Dat wil zeggen dat als we massa (en dus energie) aan het zwarte gat toevoegen, de temperatuur van het zwarte gat afneemt. Grote zwarte gaten zijn dus kouder dan kleine zwarte gaten! Hiermee komen we de eerste bijzondere thermodynamische eigenschap van zwarte gaten tegen. Voor verreweg de meeste thermodynamische systemen is het zo dat de temperatuur toeneemt als we er energie aan toevoegen. De verhouding tussen temperatuurtoename en toegevoegde energie wordt ook wel ‘warmtecapaciteit’ genoemd. Voor vrijwel alle thermodynamsche systemen (denk aan containers met gas, koppen thee, enzovoort) is deze warmtecapaciteit positief: de temperatuur neemt toe als we energie toevoegen. Zwarte gaten zijn in dit opzicht een vreemde eend in de bijt: ze hebben een negatieve warmtecapaciteit – hun temperatuur neemt af als we energie toevoegen.

Naar boven

Entropie

In de thermodynamica zijn we niet alleen geïnteresseerd in de temperatuur van objecten – dat zou van de thermodynamica wel een heel saaie wetenschap maken. Thermodynamica houdt zich veel algemener bezig met macroscopische eigenschappen van systemen die uit een heel groot aantal microscopische componenten bestaan. Denk aan het gas in een gasfles: dat bestaat uit een enorm aantal atomen, die we onmogelijk allemaal afzonderlijk kunnen beschrijven en observeren. Samen leiden al die atomen echter tot een aantal macroscopisch waarneembare eigenschappen van het gas. De temperatuur van het gas is er daar een van, maar we kunnen bijvoorbeeld ook het totale volume of de druk van het gas bestuderen. De thermodynamica onderzoekt de verbanden die tussen dergelijke macroscopische grootheden bestaan. Een voorbeeld van een thermodynamische wet is bijvoorbeeld: als de temperatuur van een gas toeneemt, neemt ook de druk van het gas toe. (Wie wel eens met een hogedrukpan gekookt heeft, is ongetwijfeld bekend met dit verschijnsel.)

De thermodynamische grootheid waarin we in de komende artikelen met name geïnteresseerd zullen zijn, is uit het dagelijks leven iets minder bekend dan druk, volume en temperatuur. Die grootheid is de entropie van een thermodynamisch systeem. Het begrip entropie is zeer uitgebreid behandeld in een eerder dossier, speciaal over dat onderwerp. Wie alle ins en outs van het begrip wil weten, verwijzen we dus naar dat dossier. Voor dit artikel en de komende artikelen volstaan we met een korte beschrijving.

Afbeelding 2. Ludwig Boltzmann (1844-1906).Het graf van Boltzmann – de ‘vader van de entropie’ – in Wenen. Boven de buste staat de formule geschreven waarin Boltzmann weergaf dat de twee verschillende definities van entropie tot dezelfde uitkomst leiden. Foto: Wikipedia-gebruiker Daderot.

De entropie van een thermodynamisch systeem kan op twee op het oog heel verschillende manieren beschreven worden.

1. Als we energie aan een thermodynamisch systeem toevoegen (bijvoorbeeld door het gas in een zuiger te verwarmen) kan die energie op twee manieren gebruikt worden. De energie kan omgezet worden in warmte, wat inhoudt dat de atomen waaruit het gas bestaat iets harder gaan trillen of sneller door elkaar gaan krioelen. Maar de energie kan ook ‘nuttig’ gebruikt worden in de vorm van (macroscopische) arbeid: het gas in de zuiger kan uitzetten, waardoor de zuiger gebruikt kan worden om bijvoorbeeld een motor aan te drijven. Bij het toevoegen van energie aan een thermodynamisch systeem zullen in het algemeen beide verschijnselen voorkomen: een deel van de energie zal worden omgezet in warmte, en een deel in arbeid. Omgekeerd kunnen we zeggen dat de energie in een thermodynamisch systeem voorkomt in twee vormen: nutteloze warmte en ‘beschikbare energie’ die in arbeid kan worden omgezet. Het blijkt nu dat de hoeveelheid beschikbare energie voor arbeid toeneemt naarmate de temperatuur van het systeem (ten opzichte van de omgeving) toeneemt.  De verhouding tussen deze twee grootheden is constant, en wordt de entropie genoemd. Entropie is dus zoiets als ‘hoeveelheid beschikbare energie per graad temperatuurverschil ten opzichte van de omgeving’.
2. Een macroscopisch systeem kan vaak op heel veel verschillende manieren uit microscopische bouwstenen worden opgebouwd. Bijvoorbeeld: als ik van een gas alle macroscopische eigenschappen (temperatuur, volume, druk, enzovoort) ken, weet ik nog niet precies van elk atoom op welke plaats het zich bevindt en met welke snelheid het beweegt. Er zijn enorm veel verschillende microscopische configuraties mogelijk die allemaal tot een systeem met dezelfde druk, temperatuur, enzovoort leiden. Een interessante vraag is dus: als ik alle macroscopische eigenschappen van een thermodynamisch systeem beschrijf, hoeveel microscopische configuraties bestaan er dan die tot deze macroscopische eigenschappen leiden? Dit aantal heet de entropie van het systeem. (De kleine lettertjes: (1) Eigenlijk moeten we – zoals uitgelegd in dit artikel – de logaritme van het aantal microscopische toestanden nemen om exact de entropie te vinden. (2) Wie zich zorgen maakt over het feit dat atomen in een gas zich op oneindig veel plaatsen kunnen bevinden zodat het ‘aantal microscopische toestanden’ dus oneindig groot lijkt te zijn, kan in hetzelfde artikel lezen hoe dat probleem wordt opgelost.) Volgens deze definitie is entropie zoiets als ‘het aantal microscopische toestanden dat overeenkomt met een gegeven macroscopische toestand’.

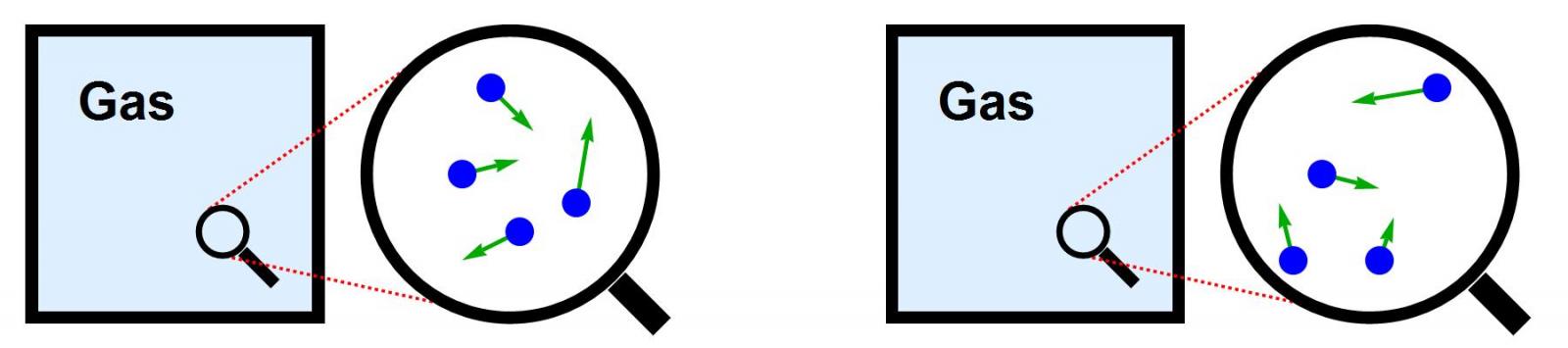
Afbeelding 3. De microscopische definitie van entropie.Een macroscopisch systeem, zoals een gas, kan op heel veel verschillende microscopische manieren opgebouwd worden: atomen kunnen bijvoorbeeld allerlei verschillende posities en snelheden hebben die leiden tot dezelfde temperatuur, druk, enzovoort. De entropie beschrijft het aantal manieren waarop een macroscopisch systeem microscopisch opgebouwd kan worden.

Uit deze twee definities zal het absoluut niet duidelijk zijn dat het hier tweemaal om precies dezelfde grootheid gaat! Het feit dat de twee definities van entropie toch tot dezelfde uitkomst leiden (iets preciezer: op een schaalfactor na, die we hierboven al tegenkwamen en die k_B genoemd wordt) werd in 1877 bewezen door de Oostenrijkse natuurkundige Ludwig Boltzmann.

Naar boven

Heeft een zwart gat een entropie?

Zoals we in met name de eerste definitie van entropie (‘hoeveelheid beschikbare energie per graad temperatuurverschil’) kunnen zien, hebben temperatuur en entropie heel veel met elkaar te maken. Nu we weten dat ook zwarte gaten een temperatuur hebben, ligt de vraag dus voor de hand of zwarte gaten ook een bijbehorende entropie hebben.

Afbeelding 4. De entropie van een zwart gat.Op macroscopische schaal lijkt een zwart gat entropie te hebben. Maar kunnen we ook een microscopische beschrijving ervan vinden – kunnen we de toestanden van het zwarte gat tellen? Afbeelding: Tim Bakker.

Vanuit de ‘macroscopische’ definitie lijkt het antwoord ja erg voor de hand te liggen. Een zwart gat kan inderdaad arbeid verrichten – bijvoorbeeld door zijn horizon te vergroten en daarbij de ruimte om zich heen meer of minder te krommen. Hoeveel arbeid het zwarte gat kan daarbij verricht hangt af van de grootte van de horizon, dus van de massa, en dus van de temperatuur. Kortom: er is een duidelijk verband tussen temperatuur en ‘beschikbare energie voor arbeid’, en dus verwachten we dat een zwart gat een entropie heeft.

Vanuit de ‘microscopische’ definitie van entropie ligt dit antwoord echter veel minder voor de hand. Het is duidelijk wat de macroscopische eigenschappen zijn die een zwart gat heeft: het heeft een massa, een volume (dat van de horizon), een temperatuur, en eventueel een elektrische lading of bijvoorbeeld een rotatiesnelheid. Maar hoeveel microscopische configuraties zijn er die tot zo’n macroscopisch zwart gat leiden? Of nog basaler: wat zijn eigenlijk de microscopische bouwstenen waaruit een zwart gat is opgebouwd? Van buiten het zwarte gat bekeken zien alle zwarte gaten met een bepaalde massa, lading, enzovoort er exact hetzelfde uit! Het enige dat we buiten de horizon van een zwart gat kunnen waarnemen is de kromming van de ruimtetijd – alle ‘microscopische’ informatie over waaruit het zwarte gat is gevormd is voor de externe waarnemer verloren. Er lijken voor de externe waarnemer dus helemaal geen microscopische toestanden te bestaan die we kunnen tellen – vanuit dit oogpunt lijkt het dus heel lastig om de entropie volgens onze tweede, microscopische definitie te bepalen.

De twee belangrijke vragen zijn dus: heeft een zwart gat echt een thermodynamische entropie, en zo ja, zijn er dan ook microscopische toestanden die we kunnen tellen om tot die entropie te komen? De eerste vraag is betrekkelijk eenvoudig te beantwoorden. In het eerstvolgende artikel zullen we nog iets preciezer kijken naar de thermodynamische eigenschappen van zwarte gaten, en zullen we zien dat een zwart gat inderdaad een entropie lijkt te hebben. De tweede vraag – wat de bijbehorende microscopische toestanden zijn – is een vraag die theoretisch fysici al decennialang intensief bezighoudt, en waarop nog altijd geen volledig en algemeen geaccepteerd antwoord bekend is. In de artikelen die volgen op het komende artikel zullen we diverse mogelijke antwoorden op deze vraag bespreken.

Naar boven

In het elfde artikel in dit dossier bespreken we de thermodynamica van zwarte gaten.