Zwarte gaten (4): Hawkingstraling

In dit artikel:

• Het vacuüm
• Het Unruh-effect
• Het equivalentieprincipe
• Hawkingstraling

Het vacuüm

Bij het woord “vacuüm” denken we in het algemeen aan volkomen lege ruimte. Uit quantummechanisch oogpunt is dat beeld echter verre van juist. In het dossier over quantummechanica is besproken dat de ruimte om ons heen niet leeg is, maar gevuld met allerlei verschillende velden. Het elektromagnetische veld is daar het bekendste voorbeeld van, maar er zijn er nog veel meer: bij elke fundamentele kracht en elk elementair deeltje in de natuur hoort een veld. Zowel krachten als deeltjes kunnen we in de quantummechanica zien als golven die zich door die velden voortplanten.

Afbeelding 1. Een klassieke vacuümpomp.In de klassieke natuurkunde wordt een vacuüm gezien als een stuk ruimte dat helemaal leeg is. In de quantummechanica blijkt een vacuüm echter nooit helemaal leeg: het bevat altijd velden, en er ontstaan en verdwijnen continu deeltjes. Afbeelding: Schulhistorische Sammlung, Bremerhaven, Duitsland.

Quantummechanica is bovendien een theorie van kansprocessen. Er bestaat geen toestand waarin alle quantumvelden volkomen in rust zijn en dat voor altijd blijven: er is altijd een kans dat in een verder lege ruimte een veld ineens een trilling vertoont, en dat er daardoor bijvoorbeeld twee deeltjes ontstaan. Een enkel deeltje kan in het algemeen niet ontstaan, omdat er in de natuur allerlei behoudswetten zijn. Denk aan het behoud van lading: als er uit het niets een deeltje met positieve lading ontstaat, zal er tegelijkertijd een deeltje met negatieve lading moeten ontstaan. Zo gelden er veel meer behoudswetten; het resultaat is dat een deeltje altijd alleen tegelijk met zijn antideeltje, met al die eigenschappen tegengesteld, kan ontstaan.

Het beeld van een vacuüm als volkomen lege en statische ruimte is dus in de quantummechanica heel misleidend. Ook in “zo leeg mogelijke ruimte” zijn allerlei velden aanwezig, en ontstaan en verdwijnen op microscopische schaal continu paren van deeltjes en hun antideeltjes. Toch bestaat er ook in de quantummechanica wel degelijk een toestand die we het “vacuüm” noemen. Daarvoor geldt precies wat we hiervoor zeiden: die toestand beschrijft geen lege ruimte, maar wel een ruimte die zo leeg mogelijk is. Iets preciezer: het vacuüm in de quantummechanica is de toestand van een stuk ruimte die van alle mogelijke toestanden de laagst mogelijke energie heeft.

Daarmee hebben we in de quantummechanica dus een ander begrip van het vacuüm dan in de klassieke natuurkunde. Echt interessant wordt het echter pas als we ook de relativiteitstheorie in ons verhaal betrekken: dan blijkt dat vacuüm opeens allerlei heel verrassende eigenschappen te hebben!

Naar boven

Het Unruh-effect

Een heel bijzondere eigenschap van het vacuüm werd in de jaren ’70 beschreven door een drietal fysici: de Amerikaan Stephen Fulling, de Engelsman Paul Davies, en de Canadees William Unruh. Het effect werd uiteindelijk naar de laatste van deze drie het Unruh-effect genoemd.

Afbeelding 2. William Unruh.William Unruh (geb. 1945) was een van de drie natuurkundigen die als eerste beschreven hoe voor een versnelde waarnemer het vacuüm een temperatuur krijgt. Afbeelding: wikipedia-gebruiker Childrenofthedragon.

Het Unruh-effect is een gevolg van een centrale eigenschap van de relativiteitstheorie: natuurkundige grootheden kunnen voor verschillende waarnemers verschillende waarden aannemen. De bekendste voorbeelden hiervan zijn waarschijnlijk Lorentzcontractie – het feit dat onderling bewegende waarnemers verschillende lengtes voor één en hetzelfde voorwerp kunnen meten – en tijdsdilatatie – het feit dat onderling bewegende waarnemers verschillende tijdsintervallen tussen twee gebeurtenissen kunnen meten.

Ook over andere natuurkundige grootheden kunnen waarnemers het echter oneens zijn. Eén van deze grootheden is energie. De energie van een bepaald proces – of een bepaalde toestand – kan door onderling bewegende waarnemers als heel verschillend gemeten worden. Wat Fulling, Davies en Unruh lieten zien, was dat dit zelfs zo ver kon gaan dat waarnemers het oneens kunnen zijn over welke van twee mogelijke processen of toestanden de laagste energie heeft. Dit gebeurt niet als de waarnemers met constante snelheid ten opzichte van elkaar bewegen, maar kan wel voorkomen als een van de twee versnelt. Dat heeft natuurlijk belangrijke gevolgen voor onze definitie van het quantummechanische vacuüm: als een eerste waarnemer een bepaald stuk ruimte in de toestand met de laagst mogelijke energie ziet, kan een ten opzichte van hem versnellende waarnemer het daarmee oneens zijn, en de vacuümbrij van velden en deeltjes zien in een toestand die niet de laagst mogelijke energie heeft. Met andere woorden: voor deze versnellende waarnemer is precies hetzelfde stuk ruimte helemaal niet in een vacuümtoestand!

Unruh wist dit nogal gecompliceerde resultaat te beschrijven in een betrekkelijk eenvoudige formule. Hij liet zien dat een waarnemer die met een versnelling a beweegt door een ruimte die door een niet versnellende waarnemer als het vacuüm wordt ervaren, ziet dat de ruimte enigszins “opwarmt” en voor hem de volgende temperatuur T krijgt:

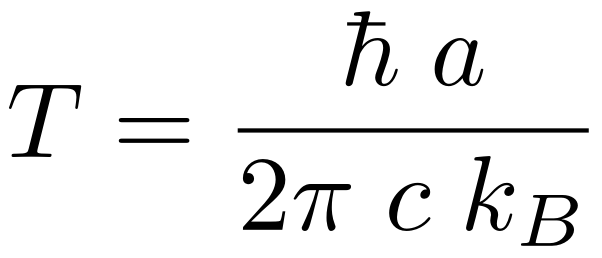
In deze formule komen naast de versnelling a en de temperatuur T alleen nog een aantal natuurconstantes voor: de constante van Planck, ħ; de lichtsnelheid, c; en de constante van Boltzmann, k_B. Met name het verschijnen van zowel de constante van Planck als de lichtsnelheid is veelzeggend: daaruit blijkt dat het hier gaat om een verschijnsel waarin zowel de quantummechanica als de relativiteitstheorie een centrale rol spelen.

Samenvattend: een waarnemer die met een bepaalde versnelling door een “vacuüm” beweegt, ziet helemaal geen zo leeg mogelijke ruimte. Hij ziet een medium met een bepaalde temperatuur – de Unruh-temperatuur – en hij ziet dit “nep-vacuüm” dus ook een hoeveelheid straling uitzenden (bestaande uit de eerder genoemde paren van deeltjes en antideeltjes) die behoort bij die temperatuur.

Naar boven

Het equivalentieprincipe

De ontdekking van Unruh en zijn collega’s was op zich al heel verrassend en interessant, maar het verhaal wordt nóg interessanter als we er ook het equivalentieprincipe in betrekken. Dit belangrijke beginsel uit de algemene relativiteitstheorie hebben we in het dossier over die theorie al uitgebreid besproken, dus in dit artikel behandelen we het slechts kort. Het equivalentieprincipe was de observatie van Einstein dat er nauwelijks verschil is tussen waarnemers die zich in een zwaartekrachtsveld bevinden, en waarnemers die zich niet in zo’n veld bevinden, maar die versneld worden. Afbeelding 3 geeft een illustratie hiervan: links zien we een waarnemer die, in een afgesloten lift in een verder lege ruimte, omhoog versneld wordt. De waarnemer ziet een bal, die in de ruimte stilstaat, ten opzichte van hemzelf omlaag versneld worden. Het is dus precies alsof de bal valt onder invloed van een zwaartekrachtsveld, zoals in het rechterplaatje gebeurt.

Afbeelding 3. Het equivalentieprincipe.Links ziet een waarnemer in een versnelde lift een bal die stilstaat in de ruimte. Rechts ziet een waarnemer in een zwaartekrachtsveld een bal in vrije val. De twee waarnemers zien de ballen op exact dezelfde manier “vallen”.

In dit experiment kunnen de waarnemers dus niet het verschil bepalen tussen versnelde beweging en een zwaartekrachtsveld, en het cruciale inzicht van Einstein was dat dit in geen enkel experiment kan: alle natuurwetten in een versnelde lift zijn exact gelijk aan diezelfde natuurwetten in een zwaartekrachtsveld. Die observatie heeft grote gevolgen als we die ook toepassen op het Unruh-effect.

Naar boven

Hawkingstraling

We kunnen aan de hand van de bovenstaande feiten verwachten dat voor een waarnemer die zich in een zwaartekrachtsveld bevindt, een vacuüm ook een bepaalde temperatuur zal hebben. Laten we dat iets nauwkeuriger formuleren: het equivalentieprincipe geldt voor waarnemers die stilstaan in een zwaartekrachtsveld – met andere woorden: waarnemers die niet in vrije val met de zwaartekracht meebewegen, maar die tegen de zwaartekracht in op dezelfde plek blijven, net zoals de rechter waarnemer in afbeelding 3 dat doet. We zouden verwachten dat een dergelijke waarnemer een verder “lege” ruimte dus niet als volkomen leeg ervaart, maar dankzij het Unruh-effect als een medium met een bepaalde temperatuur dat een bepaalde straling uitzendt.

De eerste die in een duidelijke berekening liet zien dat we zoiets inderdaad kunnen verwachten, was de bekende Engelse natuurkundige Stephen Hawking, in 1974. Hawking gebruikte voor zijn berekening een systeem waarvan we weten dat er een groot zwaartekrachtsveld is: een zwart gat. Hij liet zien dat een waarnemer die net buiten de horizon van een zwart gat “zweeft” (en dus eigenlijk heel hard naar buiten versnelt om niet het zwarte gat in gezogen te worden) de op het oog lege ruimte die dat zwarte gat in zich opzuigt ervaart als een medium vol straling met een bepaalde temperatuur. Vervolgens toonde hij aan dat een deel van deze straling – die zich immers buiten de horizon bevindt – ook daadwerkelijk aan het zwarte gat kan ontsnappen, en ook waarnemers op grote afstand kan bereiken. Met andere woorden: zodra we zowel de quantummechanica (die ons vertelt wat een vacuüm is) als de relativiteitstheorie (die ons vertelt hoe we dat vacuüm waarnemen) in het verhaal meenemen, zien we dat een zwart gat helemaal niet echt zwart is, maar langzaam straling uitstraalt! Op deze manier ontsnapt er tóch langzaam energie (en vanwege E=mc² dus ook massa) aan het zwarte gat.

Afbeelding 4. Stephen Hawking.Stephen Hawking (geb. 1942) besefte als eerste dat de combinatie van quantummechanica en relativiteitstheorie ertoe leidt dat zwarte gaten toch straling uitzenden en dus langzaam kunnen “verdampen”.

Deze beschrijving roept natuurlijk allerlei vragen op. Hoe slaagt de energie, vanuit het zwarte gat zelf gezien, erin om “uit het zwarte gat te ontsnappen”? Kan een zwart gat op deze manier helemaal “verdampen”, en blijft er dan helemaal niets over? Hoe ziet een waarnemer die wél in vrije val is het verdampen van het zwarte gat? Nadat Hawking in 1974 zijn berekening gedaan had, begonnen natuurkundigen zich over al deze vragen het hoofd te breken. Op een groot deel van die vragen weten we inmiddels een goed antwoord, maar het zou te ver gaan om te zeggen dat we inmiddels alle ins en outs van de Hawkingstraling helemaal begrijpen. Sterker nog: het goed begrijpen van dit verschijnsel is een van de belangrijkste onderzoeksvragen in de theoretische natuurkunde van dit moment.

In het volgende artikel in deze serie beginnen we met het beschrijven van de huidige zoektocht naar een goed begrip van zwarte gaten en hun Hawkingstraling. We doen dat  aan de hand van een eerste raadsel dat die straling met zich meebrengt: de informatieparadox.

Naar boven

In het vijfde artikel in deze serie bespreken we de informatieparadox.