Zwarte gaten (11): Zwarte gaten en thermodynamica

In dit artikel:

• De eerste hoofdwet van de thermodynamica
• De tweede hoofdwet van de thermodynamica
• De derde en de ‘nulde’ hoofdwet
• Een raadsel

Afbeelding 1. Twee zwarte gaten vormen samen een nieuw zwart gat.We zullen in dit artikel zien dat zwarte gaten voldoen aan alle wetten van de thermodynamica. Het samenvoegen van zwarte gaten is dus vergelijkbaar met het samenvoegen van twee thermodynamische systemen – denk aan het mengen van twee vloeistoffen of gassen met bijvoorbeeld verschillende temperatuur en volume. Afbeelding (artist impression): NASA.

De eerste hoofdwet van de thermodynamica

Alle thermodynamische systemen voldoen aan een aantal belangrijke natuurwetten, die in de loop van de 19e eeuw door diverse natuurkundigen werden beschreven. Deze wetten zijn zo universeel geldend dat ze tegenwoordig de ‘hoofdwetten van de thermodynamica‘ worden genoemd. Zoals we zullen zien, speelt entropie in deze wetten een cruciale rol. We kunnen de vraag aan het begin van het artikel dus iets verfijnen, en haar stellen als: ‘voldoen zwarte gaten aan de hoofdwetten van de thermodynamica’?

Laten we om te beginnen eens kijken naar de eerste hoofdwet van de thermodynamica. Die wet vertelt ons waar de energie van een thermodynamisch systeem vandaan komt. In het eenvoudigste geval ziet de eerste hoofdwet in formulevorm er als volgt uit:

In woorden zegt deze formule het volgende: als de entropie van een systeem met een hoeveelheid δS verandert, verandert de energie van het systeem met een hoeveelheid δE, die we kunnen uitrekenen door de entropieverandering met de temperatuur T te vermenigvuldigen. Wie deze zin nogmaals leest, zal ontdekken dat hier vrijwel hetzelfde staat als wat we in onze definitie van entropie zeiden toen we entropie beschreven als ‘hoeveelheid beschikbare energie per graad temperatuurverschil’. Overigens kunnen we aan een thermodynamisch systeem natuurlijk veel meer veranderen dan de entropie: we zouden bijvoorbeeld ook de temperatuur of de druk kunnen veranderen. Als we dergelijke veranderingen ook toestaan, krijgt de bovenstaande formule een ingewikkelder vorm (die uiteindelijk altijd neerkomt op het principe dat energie behouden is), maar voor dit artikel volstaat de bovenstaande eenvoudige vorm.

De vraag is nu: kunnen we voor zwarte gaten, waarvan we verwachten dat ze ook een entropie hebben, een soortgelijke natuurwet vinden? Het antwoord is dat er in elk geval een natuurwet voor zwarte gaten is die erg op de eerste hoofdwet lijkt. Die wet beschrijft de verandering in het oppervlak van het zwarte gat (iets preciezer: de verandering in het oppervlak van de horizon, δA) als we een hoeveelheid energie δE aan het zwarte gat toevoegen. In formulevorm ziet die natuurwet er als volgt uit:

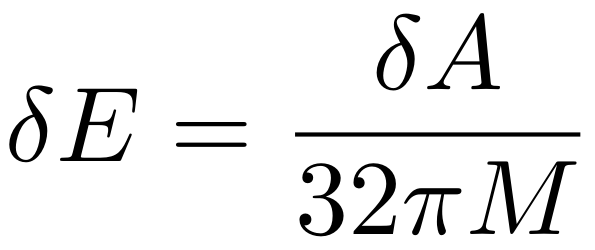
In woorden: een oppervlaktetoename δA voor een zwart gat kunnen we bewerkstelligen door een hoeveelheid energie δE in het zwarte gat te laten vallen. Die hoeveelheid energie rekenen we uit door δA te delen door 32 maal π maal de massa M van het zwarte gat.

Deze laatste wet lijkt wel een beetje op de eerste hoofdwet van de thermodynamica, maar de overeenkomsten zijn misschien nog niet erg overtuigend. We kunnen die overeenkomsten veel overtuigender maken door ons te herinneren wat de temperatuur van een zwart gat ook alweer was. In het vorige artikel kwamen we de formule tegen (in slim gekozen eenheden – dezelfde eenheden die voor de formules hierboven gelden) die Stephen Hawking voor die temperatuur afleidde. Die formule was

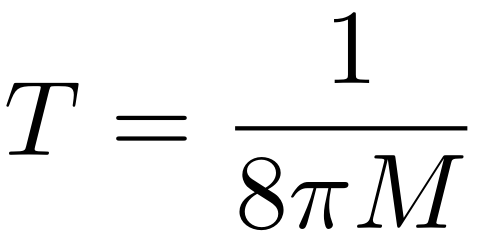
We zien dat de temperatuur T van een zwart gat van zijn massa M afhangt en dat dit, op een factor 4 na, precies de combinatie is die in de vorige formule voor de energietoename voorkomt! Met andere woorden, we kunnen die formule ook schrijven als

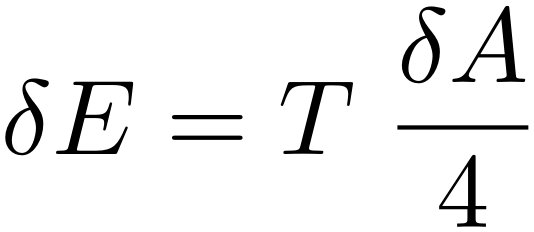
en daarmee lijkt deze formule al een heel stuk meer op de eerste hoofdwet van de thermodynamica! Het verschil tussen de twee wetten is nog dat waar in de eerste hoofdwet de entropietoename δS stond, in de wet voor zwarte gaten de oppervlaktetoename (gedeeld door 4), δA/4 staat.

Deze ‘bug’ blijkt een ‘feature’ te zijn. We vermoedden immers al dat een zwart gat een entropie zou hebben, maar hadden nog geen idee hoe we deze entropie konden meten. Aan de hand van het vergelijken van de bovenstaande formules ligt het nu voor de hand hoe we dat zouden kunnen doen: als de entropie van een zwart gat gelijk is aan een kwart van zijn oppervlak, is de bovenstaande formule niets anders dan de eerst hoofdwet van de thermodynamica!

De eerste die deze gelijkenis opviel, aan het begin van de jaren ’70, was de Mexicaans-Israelische natuurkundige Jacob Bekenstein. Zijn werk, in combinatie met dat van Stephen Hawking, leidde uiteindelijk tot de bovenstaande conclusie: het lijkt erop dat een zwart gat inderdaad een entropie, S, heeft, en dat die entropie om te voldoen aan de eerste hoofdwet van de thermodynamica (in de slim gekozen eenheden die we in het vorige artikel beschreven) gelijk moet zijn aan

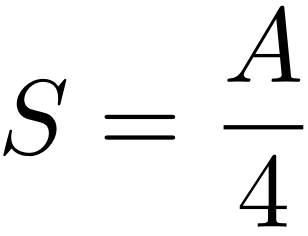
Deze uitdrukking voor de entropie S in termen van het oppervlak A wordt sindsdien dan ook de Bekenstein-Hawkingentropie van het zwarte gat genoemd.

Afbeelding 2. Jacob Bekenstein.Het werk van Bekenstein leidde samen met dat van Stephen Hawking tot de formule die de entropie van zwarte gaten beschrijft.

Wie van al dit gegoochel met formules nog niet erg onder de indruk is, heeft geen ongelijk: hoewel we hiermee een nieuwe hint vinden voor wat de entropie van zwarte gaten nu precies is, hebben we natuurlijk nog alles behalve een volledige, sluitende theorie van de thermodynamica van zwarte gaten. We zullen dus nog heel wat meer hints moeten verzamelen, en doen dat allereerst door te kijken naar de andere hoofdwetten van de thermodynamica.

Naar boven

De tweede hoofdwet van de thermodynamica

Ook de tweede hoofdwet van de thermodynamica gaat over entropie. Die wet zegt dat voor algemene thermodynamische systemen de entropie in de loop van de tijd nooit afneemt – dus ofwel gelijk blijft, ofwel toeneemt. Voor wie van formules houdt: in wiskundige termen beschrijven we dat in termen van een tijdsafgeleide van de entropie als

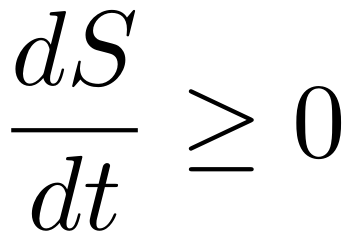
De vraag is: is deze hoofdwet consistent met wat we nu vermoeden over zwarte gaten – namelijk dat ze een entropie hebben die gelijk is aan een kwart van hun oppervlak? Het antwoord is ja: ook voor de horizon van een zwart gat geldt immers dat die altijd groeit naarmate het zwarte gat meer opslokt! Ook het oppervlak van een zwart gat neemt dus nooit af – weer in formulevorm:

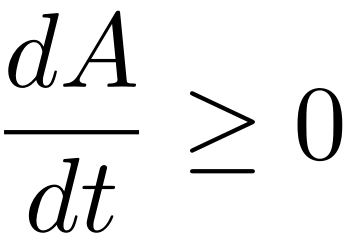
Onze aanname dat de entropie van een zwart gat gegeven wordt door een kwart van zijn oppervlak is dus volkomen consistent met de tweede hoofdwet van de thermodynamica. (De factor 4 maakt daarin natuurlijk geen verschil: als het oppervlak nooit afneemt, doet een kwart van het oppervlak dat ook niet.)

Afbeelding 3. Nicolas Léonard Sadi Carnot (1796-1832).Sadi Carnot (op de afbeelding 17 jaar oud) was in 1824 de eerste die de tweede hoofdwet van de thermodynamica beschreef. Schilderij van Louis-Léopold Boilly.

Mogelijk maken heel oplettende lezers zich nu zorgen over het verschijnsel Hawkingstraling. We hebben immers gezien dat een zwart gat heel langzaam straling kan uitzenden en daarbij kan verdampen. Neemt het oppervlak van het zwarte gat daarbij niet af? Dat doet het inderdaad, maar de sleutelwoorden in deze zin zijn ‘heel langzaam’. In fysische zwarte gaten zoals we die in het heelal tegenkomen, zullen de quantummechanische Hawkingeffecten volledig verdwijnen ten opzichte van de ‘macroscopische’ energie die een zwart gat opslokt, en zal het oppervlak van een zwart gat dus altijd toenemen. Op meer fundamenteel niveau is het natuurlijk wel van belang dat we de quantumeffecten die Hawking beschreef ook begrijpen in termen van entropie. Het zal uiteindelijk blijken dat deze microscopische effecten betekenen dat de relatie S = A/4 niet helemaal juist is, maar dat ook op deze relatie microscopisch kleine quantumcorrecties bestaan. Voor dit moment maken we ons over deze quantumcorrecties echter nog geen zorgen, en gaan we verder met de heel goede benadering die zegt dat de entropie van een zwart gat een kwart van zijn oppervlak is.

Naar boven

De derde en de ‘nulde’ hoofdwet

Zowel de eerste als de tweede hoofdwet van de thermodynamica leiden ons dus tot de conclusie dat de entropie van een zwart gat heel veel te maken heeft met de grootte van het oppervlak van zijn horizon. Zijn er nog meer thermodynamische wetten? Jazeker: er is ook een derde hoofdwet, en in zekere zin ook nog een ‘nulde’.

De derde hoofdwet van de thermodynamica zegt dat alle thermodynamische systemen een kleinst mogelijke entropie kennen, en dat die entropie bereikt wordt bij de laagst mogelijke temperatuur van het systeem.

Voor zwarte gaten weten we dat de temperatuur afhangt van de massa, en dat de temperatuur afneemt naarmate de massa toeneemt. Het lijkt op het eerste gezicht dus erg lastig om een zwart gat van minimale temperatuur te maken: we kunnen immers altijd de massa verder doen toenemen. Bovendien neemt het oppervlak (onze voorgestelde ‘entropie’) daarbij juist toe. Hoe kan deze wet dus juist zijn voor zwarte gaten?

Het antwoord op dit raadsel zit hem in het feit dat de zwarte gaten die we tot nu toe bestudeerd hebben wel heel eenvoudig zijn: ze hebben een massa, maar bijvoorbeeld geen lading of draaisnelheid. Een gevolg daarvan is dat het oneindig veel energie kost om een zwart gat met temperatuur 0 te maken. Als we ons verhaal zouden uitbreiden naar zwarte gaten die ook een lading of een draaisnelheid hebben, blijkt het veel makkelijker te worden om een minimale temperatuur te bereiken. Er bestaan dan zogenaamde ‘extreme’ zwarte gaten die bij een gegeven massa een minimale temperatuur hebben. We kunnen die temperatuur veranderen door ofwel de lading ofwel de draaisnelheid van het zwarte gat te veranderen, maar dan blijken er twee dingen te veranderen: de temperatuur neemt toe, en het oppervlak van het zwarte gat neemt toe. Met andere woorden: deze veel ruimere (en veel meer realistische) klasse van zwarte gaten  heeft inderdaad een minimaal oppervlak, en dat minimale oppervlak wordt bereikt bij een minimale temperatuur. Ook aan de derde wet van de thermodynamica is dus voldaan als we oppervlak (zoals steeds: gedeeld door 4) identificeren met entropie!

Afbeelding 4. Een hete kop koffie.Als we lang genoeg wachten zal de koffie dezelfde temperatuur aannemen als de omgeving. Dit is een voorbeeld van de ‘nulde’ hoofdwet van de thermodynamica. Foto: Padurariu Alexandru.

De ‘nulde wet’ van de thermodynamica (die soms wel en soms niet wordt toegevoegd – vandaar de wat vreemde nummering) zegt dat een thermodynamisch systeem waarop we geen invloed uitoefenen uiteindelijk overal dezelfde temperatuur zal krijgen – het zogeheten ’thermodynamisch evenwicht’. Deze wet zegt niets over entropie, en is dus voor onze identificatie van entropie met oppervlak minder van belang. Toch is ook aan deze wet voldaan in het geval van zwarte gaten: we kunnen laten zien dat de temperatuur van zwarte gaten waarop we geen externe invloed uitoefenen (ook als die zwarte gaten draaien of een lading hebben) op elk punt van de horizon hetzelfde is.

Naar boven

Een raadsel

De situatie zoals we die nu beschreven hebben, komt overeen met de situatie in de theoretische natuurkunde aan het einde van de jaren ’70. Bekenstein en Hawking hadden in hun werk de eigenschappen van zwarte gaten vergeleken met de bekende thermodynamische wetten, en waren net als wij hierboven tot de conclusie gekomen dat zwarte gaten inderdaad thermodynamische systemen zijn zolang we tenminste aannemen dat hun entropie gelijk is aan een kwart van hun oppervlak.

De vraag was nu natuurlijk: hoe kunnen we deze verrassende relatie tussen oppervlak en entropie begrijpen? Op puur thermodynamische gronden kwam men wat dat betreft niet veel verder. Maar entropie heeft zoals we in het vorige artikel gezien hebben een microscopische oorsprong: de entropie is niets anders dan het aantal manieren waarop we een systeem met bepaalde thermodynamische eigenschappen (een gegeven temperatuur, druk, volume, enzovoort) kunnen opbouwen. Kortom: entropie telt het aantal microscopische toestanden dat hoort bij een gegeven macroscopische toestand.

De vraag sinds de jaren ’70 was dus: kunnen we op deze manier ook de entropie van een zwart gat begrijpen? Als we de macroscopische eigenschappen van een zwart gat (temperatuur, lading, draaisnelheid, en natuurlijk ‘entropie’, oftewel oppervlak) voorschrijven, op hoeveel manieren kunnen we zo’n zwart gat dan uit microscopische bouwstenen opbouwen?

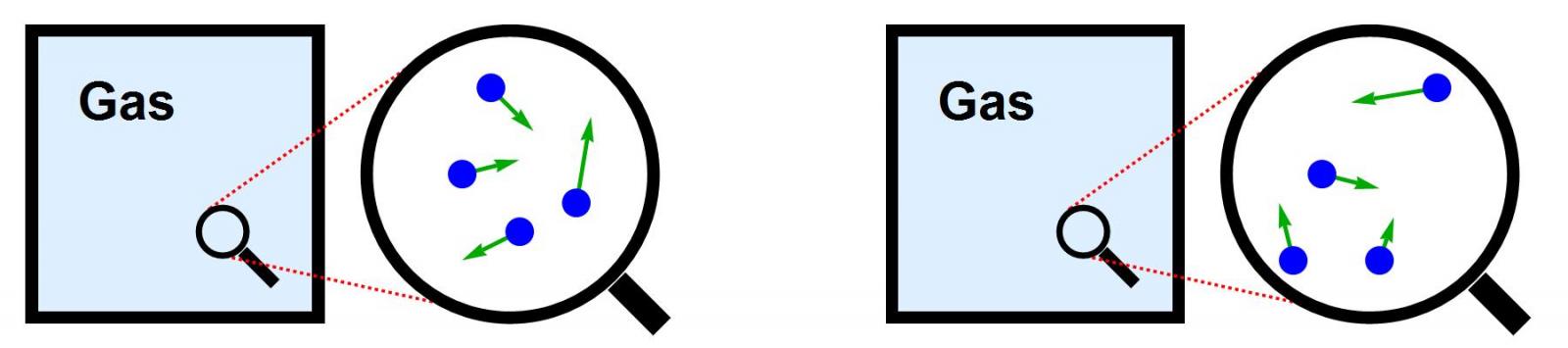
Afbeelding 5. Microscopische entropie.Entropie vertelt ons op hoeveel manieren een macroscopisch systeem (hier: een container met gas) op microscopische niveau (hier: uit bewegende moleculen) kan worden opgebouwd. Kunnen we voor een zwart gat de entropie ook op een dergelijke microscopische manier ’tellen’?

Deze vraag leidde tot een groot raadsel. Want wat zijn eigenlijk de microscopische bouwstenen van een zwart gat? En hoe kunnen we het aantal configuraties van een zwart gat tellen als alle zwarte gaten er van buitenaf gezien exact hetzelfde uitzien? We weten uit ons verhaal over de informatieparadox immers dat zwarte gaten geen enkele informatie over hun interne structuur aan de buitenwereld door lijken te geven.

Dit raadsel, dat zoals we zien het nodige met de informatieparadox te maken heeft, houdt natuurkundigen al enkele decennia bezig. Net als voor de informatieparadox geldt dat een definitief en door iedereen geaccepteerd antwoord nog altijd niet gevonden is, maar dat neemt niet weg dat er in de afgelopen tientallen jaren de nodige interessante suggesties zijn gedaan. In de komende artikelen zullen we enkele van deze suggesties bespreken.

Naar boven

In het twaalfde artikel in dit dossier bespreken we hoe Andrew Strominger en Cumrun Vafa er als eersten in slaagden om de microscopische toestanden van een zwart gat te tellen.