Zwarte gaten (12): Toestanden tellen

Afbeelding 1. Kunnen we de microscopische toestanden van een macroscopisch zwart gat tellen?Foto: Martin Vorel

In dit artikel:

• Quantumzwaartekracht
• Snaren en D-branes
• Het idee van Strominger en Vafa
• Probleem opgelost?

Quantumzwaartekracht

Op het eerste gezicht leidt de vraag uit de inleiding tot een groot raadsel. We weten immers al uit onze bespreking van de informatieparadox dat alle zwarte gaten met een bepaalde massa, lading en draaisnelheid er volgens de relativiteitstheorie exact hetzelfde uitzien. Toestanden tellen lijkt dus in zekere zin erg eenvoudig: er is in de relativiteitstheorie maar één toestand die zo’n zwart gat beschrijft. Die ene toestand is echter veel te weinig om de entropie van een zwart gat te verklaren. Op de een of andere manier moet de relativiteitstheorie dus uitgebreid worden tot een theorie waarin een zwart gat met bepaalde macroscopische parameters veel meer verschillende microscopische toestanden kan hebben.

Het ligt voor de hand welke uitbreiding we nodig hebben: de extra toestanden zullen op de een of andere manier beschreven moeten worden door de quantummechanica – de andere theorie die het gedrag van zwarte gaten bepaalt. Daarmee botsen we echter direct op het volgende probleem. Om de quantummechanische toestanden van een relativistisch systeem te beschrijven, hebben we een combinatie van beide theorieën nodig: een theorie van de quantumzwaartekracht die de quantummechanica en de relativiteitstheorie in zich verenigt.

Helaas blijkt het enorm lastig om de quantummechanica en de relativiteitstheorie in één theorie samen te voegen. Meer over de problemen die daarbij ontstaan valt te lezen in dit artikel. Op dit moment bestaat er dan ook geen algemeen geaccepteerde theorie die de quantumzwaartekracht in ons heelal beschrijft. Dat neemt niet weg dat er allerlei kandidaat-theorieën onderzocht worden; de beroemdste daarvan is waarschijnlijk de snaartheorie. De vraag is dus: kunnen we aan de hand van theorieën zoals de snaartheorie een idee krijgen van hoeveel microscopische quantumtoestanden er zijn voor een zwart gat, en hoe die quantumtoestanden eruit zien?

Naar boven

Snaren en D-branes

De eerste redelijk succesvolle poging om de quantumtoestanden van een zwart gat te tellen vond plaats in de hierboven genoemde snaartheorie. Zoals we in een recent artikel over snaartheorie beschreven, berust die theorie op de aanname dat de elementaire deeltjes in ons heelal geen puntdeeltjes zijn, maar microscopisch kleine snaartjes. (De term “microscopisch” is hier zeer figuurlijk: een gemiddelde snaar is zo’n 10^-35 meter lang, en zal er dus zelfs onder de sterkste microscoop nog als een puntje uitzien!) Met behulp van zulke snaardeeltjes blijkt het inderdaad mogelijk te zijn om de relativiteitstheorie en de quantummechanica in één raamwerk te beschrijven – al valt het nog niet mee om dat op zo’n manier te doen dat het beschreven heelal en de natuurwetten daarin lijken op ons eigen vierdimensionale heelal en de natuurwetten die daarin gelden.

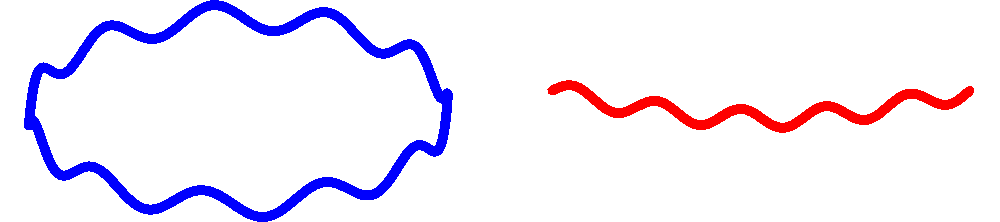
Afbeelding 2. Snaren.De microscopisch kleine snaartjes uit de snaartheorie kunnen twee vormen hebben: gesloten (links) of open (rechts).

Hoe het ook zij, het is natuurlijk interessant om te onderzoeken of de snaartheorie de entropie van zwarte gaten op zowel micro- als macroscopische schaal kan beschrijven – zelfs als die hypothetische zwarte gaten niet exact aan al onze natuurwetten voldoen. Als dat zou lukken, zou het ten eerste betekenen dat onze beschrijving van een zwart gat als een thermodynamisch systeem hout snijdt. Ten tweede zou zo’n resultaat erop wijzen dat de manier waarop de snaartheorie quantumfysica en relativiteit combineert een veelbelovende aanpak is.

Om de toestanden van een zwart gat in de snaartheorie te kunnen tellen, moeten we eerst goed begrijpen wat de fundamentele bouwstenen van die theorie zijn. De snaren zelf hebben we al genoemd, maar sinds de jaren ’90 is bekend dat snaren niet de enige bouwstenen zijn. We kunnen ons twee types snaardeeltjes voorstellen – zie afbeelding 2: gesloten snaren, die de vorm van een klein lusje hebben, en open snaren, die twee eindpunten hebben. Uit het werk van onder meer de Amerikaan Joe Polchinski (inderdaad, degene die ook mede-verantwoordelijk was voor de firewalls) bleek echter dat open snaren waarvan de eindpunten zomaar “door de ruimte zweven” geen wiskundig consistente beschrijving van de quantumzwaartekracht kunnen geven. Om dat wel te kunnen moeten die eindpunten ook daadwerkelijk ergens op eindigen. Aangezien de snaartheorie in haar eenvoudigste vorm een theorie in tien dimensies is, zijn er voor die objecten waarop de snaren kunnen eindigen nogal wat mogelijkheden. Het kunnen eendimensionale ‘staafjes’ zijn, of tweedimensionale ‘membranen’, maar de objecten kunnen ook drie, vier, vijf, tot en met negen ruimtelijke dimensies hebben. (De tiende dimensie is de tijd, waardoor al deze objecten natuurlijk bewegen.) Met een verbastering van het woord membrane werden deze objecten in de jaren ’90 D-branes gedoopt. De ‘D’ daarin staat voor de naam van de Duitse wiskundige Gustav Dirichlet: de wiskunde die de verbinding tussen de snaren en de D-branes beschrijft, werd al in de 19e eeuw (dus ver voordat de snaartheorie bestond) door hem uitgewerkt. Als we in de naam van een D-brane ook het aantal ruimtelijke dimensies willen weergeven spreken we van D1-branes, D2-branes, enzovoort.

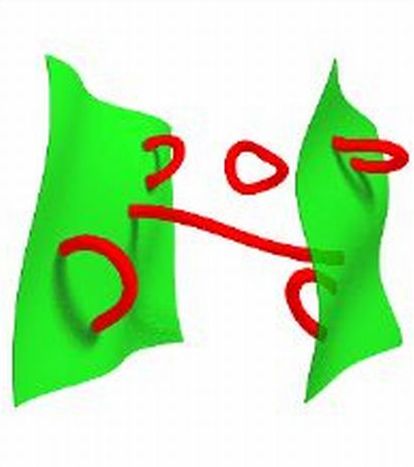
Afbeelding 3. D-branes.Snaren (in het rood) kunnen alleen eindpunten hebben als die eindpunten eindigen op een ander object: een D-brane. Hier zien we twee (groene) D2-branes. Afbeelding: via David Tong.

Naar boven

Het idee van Strominger en Vafa

Eén van de dingen die Polchinski in zijn onderzoek naar de eigenschappen van D-branes had laten zien, was dat deze objecten als ze zwaar genoeg zijn ook zwarte gaten vormen. Het lag dus voor de hand om te proberen een (hypothetisch) zwart gat op te bouwen uit snaren en D-branes, en te proberen te tellen op hoeveel manieren dit voor een gegeven zwart gat mogelijk was. Hopelijk zou de einduitkomst dan de entropie van zo’n zwart gat verklaren. Deze aanpak stuitte op twee problemen, die uiteindelijk in 1996 door de natuurkundigen Andrew Strominger en Cumrun Vafa werden opgelost.

Het eerste probleem was dat zoals gezegd de snaartheorie niet direct een beschrijving van ons heelal geeft: de theorie is bijvoorbeeld tiendimensionaal. Dat is op zich nog niet zo’n bezwaar – het correct beschrijven van een tiendimensionaal zwart gat in microscopische termen zou ook al een flinke prestatie zijn – maar daar komt nog eens bij dat ook de D-branes een groot aantal dimensies hebben. De zwarte gaten zoals wij die kennen zijn echter puntvormig (dat wil zeggen: de singulariteit in het midden is puntvormig, met een bolvormige horizon daaromheen), en dus zouden we ook in de hogerdimenionale snaartheorie graag puntvormige zwarte gaten beschrijven.

De oplossing voor dit probleem bleek betrekkelijk eenvoudig. We kunnen de dimensies van een theorie namelijk ‘oprollen’, eigenlijk op precies dezelfde manier als we bijvoorbeeld een tweedimensionaal stuk papier kunnen oprollen. Als we dat doen, krijgen we een klein kokertje, en wie dat kokertje van grote afstand bekijkt zal het zien als een ééndimensionale lijn. De tweede dimensie is nog wel aanwezig, maar is vrijwel aan onze waarneming onttrokken. Op precies dezelfde manier kunnen we één of meer dimensies van de snaartheorie oprollen, en zo een theorie construeren die op de allerkleinste schaal nog wel tiendimensionaal is, maar die er op grote schaal negen-, acht- of nog lager-dimensionaal uitziet. Bovendien kunnen we hogerdimensionale D-branes ‘mee-oprollen’ zodat we ook van deze D-branes een lager aantal dimensies zien – zie afbeelding 4. Op die manier kunnen we, door alle richtingen van een D-brane mee op te rollen met de dimensies van de snaartheorie, dus zwarte gaten ‘bouwen’ die vrijwel puntvormig zijn.

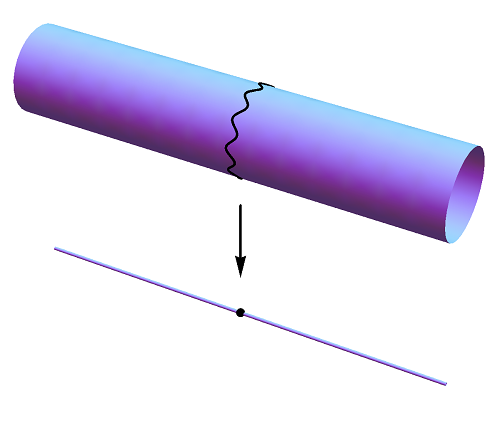
Afbeelding 4. Compactificatie.Een tweedimensionaal object, zoals een vel papier, kan worden opgerold tot een koker. Als we die koker van grote afstand bekijken zien we een lijn, en is er dus effectief één dimensie verdwenen. Wanneer een D-brane om zo’n ‘gecompactificeerde’ dimensie heen is gewikkeld, zien we van de D-brane zelf ook een dimensie minder: in dit voorbeeld ziet een D1-brane (de golvende lijn in de bovenste figuur) er na compactificatie uit als een object zonder dimensies: een punt. Strominger en Vafa gebruikten dit idee om uit hogerdimensionale D-branes puntvormige zwarte gaten te construeren.

Het tweede probleem dat Strominger en Vafa moesten oplossen was groter. We schreven hierboven namelijk dat dat D-branes zwarte gaten kunnen vormen als ze zwaar genoeg zijn. Zodra we in deze situatie zijn, is er echter direct een probleem, want in de buurt van zo’n zwart gat is de zwaartekracht zo sterk en is de ruimte zo sterk gekromd dat het wiskundig vrijwel onmogelijk wordt om de verschillende D-brane-configuraties die een zwart gat vormen te kunnen beschrijven – laat staan om ze te tellen! Voor heel lichte D-branes kunnen we aan de andere kant prima tellen op hoeveel manieren we ze samen kunnen voegen. Maar ja, een lichte verzameling van D-branes vormt weer geen zwart gat…

Strominger en Vafa losten dit probleem uiteindelijk op door te kijken naar een heel speciale klasse van D-brane-constructies. De sytemen die zij bekeken bestonden alleen uit D5-branes en D1-branes, waarbij al die D5- en D1-branes ook nog eens parallel aan elkaar moesten zijn, dus niet loodrecht of onder een andere hoek. De vijf parallelle richtingen werden vervolgens opgerold, zodat puntvormige systemen in de resterende vijf dimensies overbleven. Deze specifieke combinaties van D-branes en snaren zijn veel symmetrischer dan willekeurige combinaties – ze blijken zelfs zó symmetrisch dat juist die symmetrie (een zogenaamde supersymmetrie) ze allerlei bijzondere eigenschappen geeft.

Eén van die eigenschappen blijkt als we de zwaartekracht in de theorie langzaam opvoeren. Dit is iets wat in een model vrij eenvoudig is: elke zwaartekrachtstheorie heeft een ‘constante van Newton’ die bepaalt hoe sterk de zwaartekracht tussen twee massa’s is, en in een theoretisch model is het natuurlijk geen enkel probleem om die constante een andere waarde te geven. Het opvallende is nu het volgende. Als we D-brane-configuraties bouwen uit D5- en D1-branen en daarvan de macroscopische massa, lading en draaisnelheid bepalen, kunnen we vervolgens proberen te tellen hoeveel verschillende configuraties een gegeven massa, lading en draaisnelheid hebben. Door de supersymmetrie blijkt dit aantal niet te veranderen als we de grootte van de zwaartekracht aanpassen! De toestanden die de gegeven parameters hebben bij heel lage zwaartekracht, hebben óók allemaal dezelfde parameters bij heel hoge zwaartekracht, en andere toestanden zullen bij geen enkele zwaartekrachtsconstante precies dezelfde parameters hebben. Met andere woorden: het betreft hier een ‘geïsoleerde’ klasse van toestanden, die we naar keuze bij lage of bij hoge zwaartekracht kunnen tellen!

Zoals gezegd: bij hoge zwaartekracht – als de toestanden een zwart gat vormen – is dat tellen wiskundig vreselijk lastig, maar bij lage zwaartekracht is het betrekkelijk eenvoudig. (‘Betrekkelijk eenvoudig’ is helaas altijd nog wat te lastig om de telling in dit artikel op een begrijpelijke manier te reproduceren – wie graag naar de oorspronkelijke formules wil staren kan hier het artikel van Strominger en Vafa lezen.) Met deze ’truc’ slaagden Strominger en Vafa er dus in om het aantal toestanden van een zwart gat in de snaartheorie te tellen, en de bijbehorende entropie die ze vonden was exact gelijk aan een kwart van het oppervlak van het zwarte gat, precies zoals Bekenstein en Hawking voorspeld hadden. Met andere woorden: het was voor het eerst gelukt om de macroscopische entropie van een zwart gat aan de microscopische entropie te koppelen!

Afbeelding 5. Cumrun Vafa (links) en Andrew Strominger (rechts).Foto’s: Stephanie Mitchell / Harvard University.

Naar boven

Probleem opgelost?

Daarmee was het probleem van het tellen van quantumtoestanden van zwarte gaten natuurlijk nog niet helemaal opgelost. Zoals gezegd ging het in de berekening van Strominger en Vafa om een heel specifieke, supersymmetrische klasse van zwarte gaten, die bovendien geconstrueerd waren in een vijfdimensionale theorie waarin de natuurwetten maar heel oppervlakkig lijken op die in ons eigen heelal. Kortom: het was een enorme doorbraak om aan te tonen dat het tellen van quantumtoestanden überhaupt mogelijk was, maar aan de details moest nog flink geschaafd worden. Dat gebeurde allereerst in soortgelijke systemen binnen de snaartheorie: men vond al snel andere, meer algemene klasses van D-brane-constructies van zwarte gaten die ook geteld konden worden, en in alle gevallen bleek de uitkomst overeen te komen met de voorspelling van Bekenstein en Hawking dat de entropie gelijk was aan een kwart van het oppervlak. Daarbij werden ook systemen beschreven in vier dimensies, en systemen die niet supersymmetrisch waren, maar volledig realistische zwarte gaten zijn op deze manier toch nog altijd niet beschreven. Wellicht gebeurt dat in de toekomst nog, maar natuurkundigen zijn flexibel: als één methode niet leidt tot een volledig bevredigend resultaat komt er altijd wel iemand die een andere methode verzint. In het volgende artikel beschrijven we zo’n andere methode om het tellen van de toestanden van zwarte gaten te benaderen: fuzzballs.

Naar boven

In het dertiende artikel in dit dossier bespreken we een ander idee om de microtoestanden van zwarte gaten te beschrijven: fuzzballs.