Zwarte gaten (6): Een verloren weddenschap

In dit artikel:

• Gaat informatie verloren?
• Dualiteiten
• Holografie
• Een verloren weddenschap
• Hoe nu verder?

Afbeelding 1. John Preskill, Kip Thorne en Stephen Hawking.Hawking, Preskill en Thorne sloten in 1997 een beroemde weddenschap af over de informatieparadox. Foto: Caltech / Heidi Aspaturian.

Gaat informatie verloren?

Laten we nog eens kort het probleem samenvatten waar Hawking en zijn collega’s tegenaan liepen. Zwarte gaten kunnen in hun levensloop alles opslokken wat ze tegenkomen: planeten, sterren, nietsvermoedende ruimtevaarders – noem maar op. Toch zijn zwarte gaten geen eeuwige gevangenissen. Hawking toonde aan dat zwarte gaten ook straling uitzenden. Zodra ze niets meer opslokken, zullen zwarte gaten dus heel langzaam weer ‘verdampen’.

Het probleem is dat de eigenschappen van die Hawkingstraling alleen afhangen van de temperatuur (en dus van de massa) van het zwarte gat. De straling bevat daardoor geen enkele informatie over wat er oorspronkelijk in het zwarte gat viel. We kunnen een zwart gat vol gooien met stoelen, of met televisies; zo lang de hoeveelheid massa die we in het zwarte gat gooien maar hetzelfde is, zullen we aan de straling na afloop nooit meer kunnen zien wat het precies was dat in het zwarte gat gevallen is.

Dat levert een probleem op met een van de fundamentele beginselen van de quantummechanica en de relativiteitstheorie. Het is namelijk zo dat we in die theorieën (en in vrijwel elke andere natuurkundige theorie) uit een eindsituatie altijd terug kunnen rekenen naar de beginsituatie. Zwarte gaten lijken dit grondbeginsel te schenden: als we een zwart gat volledig laten verdampen, kunnen we nooit meer achterhalen waaruit het zwarte gat gevormd is: sterren of planeten; stoelen of televisies.

Kortom: er is een paradox ontstaan. We hebben geprobeerd om zwarte gaten te beschrijven met de quantummechanica en de relativiteitstheorie, maar het eindantwoord lijkt in tegenspraak met die theorieën. Waar wringt de schoen nu precies? Hawking en Thorne dachten dat dat bij de theorieën zelf zou zijn en dat een volledige theorie van quantumzwaartekracht uiteindelijk een theorie zou zijn waarin informatie verloren kan gaan. Preskill had meer vertrouwen in de bestaande theorieën, en dacht dat de redenering over zwarte gaten verbeterd moest worden. Bij een juiste beschouwing zou volgens hem dan blijken dat de Hawkingstraling tóch informatie bevat.

Afbeelding 2. Een ‘artist impression’ van een zwart gat.Hoewel zich rond zwarte gaten allerlei extreme processen afspelen, zijn zwarte gaten zelf zwart, en valt het dus niet mee om ze aan de sterrenhemel waar te nemen. Afbeelding: ESA.

Bij veel natuurkundige vraagstukken komt het antwoord voort uit een experiment. Als we niet weten wat er in een bepaalde situatie gebeurt, proberen we die situatie in een laboratorium te verwezenlijken, en vervolgens te meten wat er gebeurt. Dat klinkt heel eenvoudig, maar in het geval van zwarte gaten is het dat natuurlijk niet. We zijn vandaag de dag niet in staat om in een laboratorium zwarte gaten te creëren, en ze in het heelal bestuderen valt ook niet mee, om de simpele reden dat zwarte gaten zwart zijn en dus geen waarneembaar licht uitstralen. De Hawkingstraling zelf is bovendien zo zwak dat er geen hoop is dat we die op korte termijn zullen kunnen waarnemen. Het antwoord zal dus voorlopig moeten komen uit dezelfde hoek als het probleem: uit de theorie.

Naar boven

Dualiteiten

Het theoretische begrip dat uiteindelijk leidde tot het einde van de Hawking-Thorne-Preskill-weddenschap was het begrip dualiteit. Een dualiteit is een situatie waarin twee totaal verschillende natuurkundige systemen beschreven kunnen worden met exact dezelfde wiskunde.

Laten we een eenvoudig voorbeeld geven. Wie op de middelbare school natuurkunde heeft gehad, zal bekend zijn met de tweede wet van Newton:

F = m a

Deze wet uit de mechanica vertelt ons welke kracht (F) er nodig is als we een bepaalde hoeveelheid massa (m) een bepaalde versnelling (a) willen geven. Het voorschrift is eenvoudig: om die kracht te berekenen, moeten we de massa en de gewenste versnelling met elkaar vermenigvuldigen.

Een andere bekende natuurwet die op de middelbare school onderwezen wordt, is de wet van Ohm:

V = I R

Deze wet komt uit de elektriciteitsleer, en vertelt ons welke spanning (V) er nodig is om een bepaalde hoeveelheid stroom (I) door een materiaal met een bepaalde elektrische weerstand (R) te laten lopen. Ook hier is het rekenvoorschrift eenvoudig: om die spanning uit te rekenen vermenigvuldigen we de stroomsterkte met de weerstand.

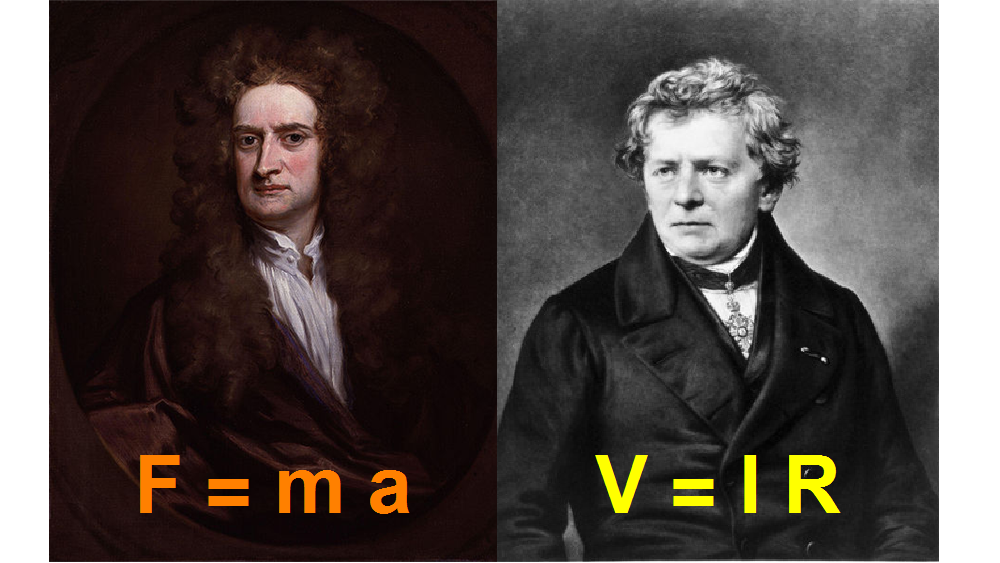
Afbeelding 3. Newton, Ohm, en de naar hen vernoemde wetten.

De precieze fysische betekenis van deze twee wetten is voor ons nu niet zozeer van belang; waar het hier om gaat is de wiskunde erachter. Die is in beide gevallen exact hetzelfde! We willen grootheid 1 uitrekenen, en om dat te doen moeten we grootheid 2 met grootheid 3 vermenigvuldigen. De symbolen en hun betekenis zijn anders, maar de wiskundige formules hierboven zijn exact gelijk.

Dit lijkt meer een toevalligheid dan een wereldschokkende observatie, en dat is het in zekere zin ook. We hebben het hier namelijk nog maar over één formule uit de mechanica (F=ma) en één formule uit de elektriciteitsleer (V=IR). Zodra we andere wetten uit diezelfde theorieën erbij nemen, zien we dat de analogie volledig spaak loopt. Zo kunnen we in de elektriciteitsleer bijvoorbeeld het vermogen (P) uitrekenen dat opgewekt kan worden door een stroom met stroomsterkte I door een materiaal met weerstand R te laten lopen. Dat vermogen is

P = I V

We kunnen ons nu afvragen: is er in de mechanica ook een soortgelijke wet? Die zou er dan als volgt uit moeten zien:

?? = m F

Eventueel zou ?? = aF ook nog kunnen, want we mogen de tweede wet van Newton natuurlijk ook schrijven als F=am; a en m zijn dus wiskundig gezien verwisselbaar. Hoe dan ook, er is in beide gevallen geen enkele wet in de mechanica die deze vorm heeft, en dus loopt de vergelijking tussen de twee theorieën hier spaak.

Het bijzondere is nu dat er paren van natuurkundige systemen zijn waarin de vergelijking niet spaak loopt. Dat wil zeggen: als we alle natuurwetten voor het ene systeem opschrijven, kunnen we daarnaast een lijstje maken van alle natuurwetten voor het andere systeem, en deze twee lijstjes zullen er wiskundig (dus op een andere naamgeving van de symbolen na) exact hetzelfde uitzien! Wanneer dit het geval is, noemen we de twee systemen duaal, en is er dus sprake van een dualiteit. Zoals we gezien hebben, zijn de mechanica en het elektromagnetisme niet duaal (daar liep het ‘lijstje’ bij de tweede vergelijking die we probeerden op te schrijven al vast), maar we zullen nu zien dat dergelijke paren van systemen wel degelijk bestaan.

Naar boven

Holografie

Paren van natuurkundige modellen die duaal zijn, liggen beslist niet voor het oprapen. De eerste die zo’n bijzonder paar van modellen vond, was de Argentijn Juan Maldacena. Hij deed dat in 1997 – toevallig het jaar waarin Hawking, Thorne en Preskill ook hun weddenschap afsloten.

Afbeelding 4. Juan Maldacena.

De modellen die Maldacena bestudeerde, zijn nogal theoretisch van aard. Aan de ene kant gaat het om een zwaartekrachtstheorie in maar liefst tien dimensies (zes meer dan onze eigen ruimte en tijd); aan de andere kant om een theorie die weliswaar een quantummechanisch systeem in de gebruikelijke vier dimensies beschrijft, maar wel een systeem dat allerlei heel bijzondere symmetrieën heeft.

De dualiteit staat bekend onder de naam “AdS/CFT-correspondentie”. De reden voor die naam is voor dit artikel niet van belang, maar voor wie op een feestje indruk wil maken: de zwaartekrachtstheorie beschrijft de zwaartekracht in een zogeheten “Anti de Sitter-ruimte” (vandaar AdS), en de vierdimensionale theorie is een quantumveldentheorie waarvan de genoemde bijzondere symmetrieën de naam conforme symmetrieën hebben gekregen (vandaar CFT: “conformal field theory”).

Een veel begrijpelijkere naam die ook vaak aan deze dualiteit wordt gegeven (en aan een hele serie soortgelijke dualiteiten die na het werk van Maldacena werden gevonden) is holografie. Die naam geeft veel beter weer wat er zo bijzonder is aan deze dualiteit: het gaat hier om twee theorieën over verschijnselen in een totaal verschillend aantal dimensies, waarvan de wiskundige beschrijving toch exact hetzelfde blijkt te zijn. De ene theorie is dus een soort “wiskundig hologram” van de ander: ook in een hologram wordt in een klein aantal dimensies (twee) een situatie in een hoger aantal dimensies (drie) beschreven.

Afbeelding 5. Een hologram.We zien twee foto’s van hetzelfde, tweedimensionale hologram, genomen uit verschillende hoeken. De muis lijkt daadwerkelijk rond te draaien: het tweedimensionale hologram is een beschrijving van een driedimensionale situatie. Hologram: Georg-Johann Lay.

Het zou te ver gaan om hier heel diep op de natuurkunde achter AdS/CFT en holografie in te gaan, dus we volstaan hier met de bovenstaande, uiterst korte beschrijving. Maar niet getreurd: in het najaar zal op deze website een uitgebreid dossier over holografie verschijnen, waarin we veel meer van de details uit de doeken zullen doen. Wie alvast in de stemming wil komen, kan het inleidende artikel van dat dossier (dat al in 2012 verscheen) hier lezen.

Naar boven

Een verloren weddenschap

Wat heeft dit alles nu met zwarte gaten te maken? Het volgende: het grote verschil in het aantal dimensies is niet het enige dat opvalt aan de duale systemen die Maldacena ontdekte. Iets anders wat heel opvallend is, is dat het aan de ene kant gaat om een zwaartekrachtstheorie, en aan de andere kant om een ‘gewone’ quantumveldentheorie – een theorie waarin de zwaartekracht geen rol speelt! Daarmee moet het dus in principe mogelijk zijn om de dualiteit te gebruiken om vragen over de zwaartekracht te ‘vertalen’ in vragen over de quantumfysica.

We verwachten dus dat het verdampen van een zwart gat op die manier omgeschreven kan worden in een ander, puur quantummechanisch proces, waarin de zwaartekracht geen enkele rol speelt. Om dit in de praktijk te doen, valt nog niet mee: het ‘woordenboek’ waarmee we vergelijkingen uit de zwaartekrachtstheorie vertalen in vergelijkingen uit de quantumtheorie is flink ingewikkeld. Om vervolgens met die vergelijkingen aan het rekenen te slaan, is nog veel ingewikkelder.

Het mooie is dat we echter helemaal geen exacte berekening hoeven te doen! De vraag waar we in geïnteresseerd zijn, is namelijk: kunnen we uit de eindsituatie, na het verdampen van een zwart gat, terugrekenen naar de beginsituatie  – de materie waaruit het zwarte gat gevormd is? En het mooie is: van pure quantumtheorieën, zonder zwaartekracht, kunnen we bewijzen dat het altijd mogelijk is om van een eindsituatie terug te rekenen naar een beginsituatie. Kortom: als de AdS/CFT-correspondentie juist is, weten we onmiddellijk dat we van elke eindsituatie in de zwaartekrachtstheorie terug kunnen rekenen naar de beginsituatie, simpelweg omdat dat in de duale quantumveldentheorie ook zo is!

Een belangrijke voorwaarde in de laatste zin is: als de AdS/CFT-correspondentie juist is. Maldacena gaf namelijk allerlei heel goede argumenten voor zijn holografische dualiteit, maar een sluitend wiskundig bewijs voor de equivalentie van de twee modellen kon hij niet geven. Dat laatste is zelfs nog altijd niet voor 100% gelukt, al is er inmiddels wel zoveel bewijsmateriaal voor de dualiteit verzameld dat nog maar weinig fysici aan de juistheid ervan twijfelen. Dat gold ook voor Stephen Hawking. Hij was er in 2004 zodanig van overtuigd dat het idee van Maldacena juist was, en dat zwarte gaten dus geen informatie konden vernietigen, dat hij de weddenschap opgaf. Zoals beloofd gaf hij John Preskill, de winnaar van de weddenschap, daarom een encyclopedie: ‘Total Baseball, the Ultimate Baseball Encyclopedia’.

Afbeelding 6. De verliezer en de winnaar.John Preskill houdt de encycopedie omhoog die hij zojuist van Stephen Hawking ontvangen heeft voor de gewonnen weddenschap. Afbeelding via de American Physical Society.

Naar boven

Hoe nu verder?

Is de hele informatieparadox daarmee opgelost? Dat zeker niet. We kunnen nog tenminste drie problemen opnoemen:

1. Zoals gezegd is het daadwerkelijk vertalen van berekeningen met behulp van de dualiteit van Maldacena geen sinecure. Hoewel we nu dus weten dat zwarte gaten geen informatie vernietigen, is nog allesbehalve duidelijk hoe zwarte gaten de informatie behouden.
2. De holografische dualiteit van Maldacena beschrijft aan de zwaartekrachtskant een model in maar liefst tien dimensies. Het is dus maar de vraag in hoeverre de fictieve tiendimensionale zwarte gaten in deze dualiteit overeenkomen met de vierdimensionale zwarte gaten die we in ons eigen heelal kunnen aantreffen. Inmiddels zijn er weliswaar andere dualiteiten gevonden waarin het zwaartekrachtsmodel meer op ons heelal lijkt, maar nog geen één waarin exact onze alledaagse zwaartekracht duaal is aan een quantumveldentheorie. Hoewel Maldacena dus liet zien dat er in quantumzwaartekrachtstheorieën in het algemeen geen informatie verloren hoeft te gaan, is dat nog niet expliciet bewezen voor ons eigen heelal.
3. Ten slotte: zoals gezegd is het idee van Maldacena weliswaar breed geaccepteerd, maar nog altijd niet volledig wiskundig bewezen.

Kortom: er valt nog voldoende te onderzoeken aan zwarte gaten en de informatieparadox, en het zou te ver gaan om te zeggen dat de paradox hiermee volkomen opgelost is. Dat was ook de mening van Kip Thorne, die aan dezelfde kant van de weddenschap stond als Stephen Hawking. Hoewel Hawking de weddenschap heeft opgegeven, heeft Thorne dat nog altijd niet gedaan. Zijn weddenschap met John Preskill loopt dus nog. We zullen zien hoe lang het nog duurt voor ons begrip van zwarte gaten zodanig goed is dat er nog een encyclopedie wordt overhandigd! En of die encyclopedie zoals de meeste mensen verwachten inderdaad van Thorne naar Preskill gaat, of misschien toch wel andersom.

Met name punt (1) hierboven is natuurlijk van belang. We hebben nu het sterke vermoeden dat zwarte gaten informatie behouden, maar we zouden heel graag weten hoe dat precies gebeurt. In de zoektocht naar het antwoord op die vraag zijn met name in de laatste jaren allerlei interessante ontdekkingen gedaan. Het dossier over zwarte gaten is hiermee dus nog verre van afgelopen – we hebben nog genoeg te vertellen!

Naar boven

In het zevende artikel in deze serie kijken we nog iets beter naar de informatieparadox en zien we wat die paradox met quantumkansen te maken heeft.