Zwarte gaten (3): Een relativistische beschrijving

In dit artikel:

• Relativistische zwarte gaten
• De Schwarzschildoplossing
• De singulariteit

Relativistische zwarte gaten

Op de horizon van een zwart gat is de ontsnappingssnelheid gelijk aan de lichtsnelheid. De relativiteitstheorie van Albert Einstein leert ons bovendien dat niets sneller kan gaan dan het licht.  De vraag ligt dus voor de hand of het überhaupt wel mogelijk is om aan een zwart gat te ontsnappen.

We eindigden het vorige artikel met deze vraag, maar zagen ook dat het niet helemaal vanzelfsprekend is dat zwarte gaten inderdaad alles in zich gevangen houden. De ontsnappingssnelheid geldt immers alleen voor voorwerpen die we een beginsnelheid geven en die daarna hun natuurlijke baan onder de invloed van de zwaartekracht volgen. Wat gebeurt er als we een raket bouwen die continu zijn motoren aan heeft staan? Of wat als we een hoge toren bouwen in het zwarte gat, om zo boven de horizon uit te komen?

Afbeelding 1. De lancering van een Ariane-raket.De hoogste snelheid die ooit bereikt is met een Ariane-raket is 10,4 km/s. Toch konden deze raketten ontsnappen aan de aardse zwaartekracht – ondanks dat de ontsnappingssnelheid van het aardoppervlak 11,2 km/s is. De reden daarvoor is dat de raket zijn motoren tijdens het opstijgen aan laat staan en dus blijft versnellen terwijl die hoger komt. Zou het op soortgelijke wijze mogelijk zijn om aan een zwart gat te ontsnappen? Foto: NASA.

Het is wederom de relativiteitstheorie die het antwoord op dergelijke vragen geeft. Wat Einstein in zijn algemene relativiteitstheorie aantoonde, is dat ruimte (en tijd) het best gezien kunnen worden als een soort vervormbaar rubber. Dat “rubber” vormt het toneel waarop de rest van de fysica zich afspeelt. Wat er op de horizon van een zwart gat gebeurt, is dat de ruimte zélf met de lichtsnelheid naar binnen wordt gezogen. Wie op dat punt probeert te ontsnappen is dus als een hardloper die over een loopband rent: de hardloper beweegt over de band, maar de band beweegt intussen snel naar achteren, zodat de hardloper effectief niet van zijn plaats komt. Hetzelfde gebeurt met licht dat aan de horizon van een zwart gat probeert te ontsnappen: het beweegt naar buiten, maar de ruimte waardoor het beweegt, wordt tegelijkertijd zo snel naar binnen gezogen dat het licht effectief “stilstaat”.

Afbeelding 2. Ruimtetijd als een loopband.De ruimte rond een zwart is als een loopband: de ruimte wordt snel naar binnen gezogen, en wie aan het zwarte gat wil ontsnappen moet dus met enorme snelheid “tegen de richting in” door die ruimte naar buiten bewegen. Afbeelding: Sole.

Daarmee wordt ook meteen duidelijk dat de eerder genoemde trucs om aan een zwart gat te ontsnappen niet werken. Ook een raket met motor kan nooit de lichstnelheid bereiken, en dus nooit snel genoeg gaan om door de naar binnen bewegende ruime het zwarte gat uit te vliegen. En het snel genoeg bouwen van een toren in die naar binnen snellende ruimte is natuurlijk al helemaal onmogelijk!

Naar boven

De Schwarzschildoplossing

De bovenstaande beschrijving aan de hand van “ruimte die naar binnen wordt gezogen” is natuurlijk erg kwalitatief. De algemene relativiteitstheorie is echter veel meer dan een grove vergelijking tussen ruimte en tijd en vervormbaar rubber: het is een heel precieze verzameling van wiskundige vergelijkingen die beschrijven hoe de ruimte en de tijd zich exact gedragen. De vraag is dus: is het mogelijk om een zwart gat ook te beschrijven als een oplossing van die wiskundige vergelijkingen?

Dat blijkt inderdaad mogelijk te zijn. Het was de in het vorige artikel al genoemde Duitse natuurkundige Karl Schwarzschild die die oplossing vond. Hij deed dat onder nogal bijzondere omstandigheden: toen Einsteins publicatie over de algemene relativiteitstheorie in 1915 – dus tijdens de Eerste Wereldoorlog -verscheen, diende Schwarzschild in het Duitse leger aan het front in Rusland. Tussen de oorlogsbedrijven door wist hij de nodige tijd vrij te maken voor de natuurkunde en leidde hij onder meer de naar hem vernoemde oplossing af. Helaas ontwikkelde hij in diezelfde periode aan het front een zeldzame huidziekte, waaraan de pas 42-jarige fysicus in 1916 zou komen te overlijden. Het is een intrigerende vraag welke andere belangrijke ontdekkingen Schwarzschild nog had kunnen doen als hij daarvoor de kans had gekregen.

Afbeelding 3. Karl Schwarzschild (1873-1916).Schwarzschild beschreef in 1915 als eerste een exacte oplossing van de vergelijkingen van Einstein. Deze oplossing beschreef een zwart gat, en wordt sindsdien naar hem genoemd.

Opvallend aan de oplossing van Schwarzschild is dat de horizon in zijn oplossing precies ligt op de plaats waar we die “klassiek” zouden verwachten: de horizon is een bol met een straal r_S, gegeven door de formule die we in het vorige artikel al tegenkwamen:

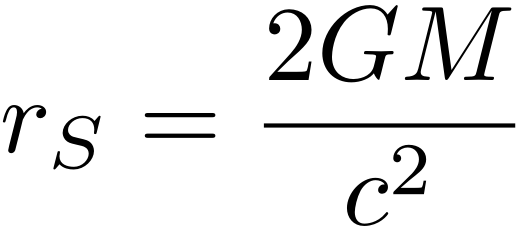
Ter herinnering: M is de massa van het zwarte gat gemeten in kilogrammen, c is de lichtsnelheid (zo’n 3,00 x 10⁸ m/s) en G is de zwaartekrachtsconstante van Newton (ongeveer 6,67 x 10^-11 m³ kg^-1 s^-2). Dat deze relativistische uitkomst precies hetzelfde is als in de “klassieke” behandeling aan de hand van een ontsnappingssnelheid, is in zekere zin bijzonder: in het algemeen zijn relativistische resultaten bij heel goede benadering hetzelfde als de klassieke antwoorden, maar zelden exact daaraan gelijk. Aan de andere kant is het lastig om kleine correctietermen in bovenstaande formule op te schrijven die de juiste eenheid (meter) hebben, dus in die zin had men de uitkomst misschien kunnen verwachten. Hoe het ook zij, de straal van de bol die de horizon van een (ongeladen, niet-roterend) zwart gat beschrijft, wordt sinds de berekening van Schwarzschild naar hem de Schwarzschildstraal genoemd.

De oplossing van Schwarzschild was niet alleen bijzonder omdat het de eerste relativistische beschrijving van een zwart gat was: het was überhaupt de eerste exacte oplossing van de vergelijkingen van Einstein die werd geconstrueerd. (Naast natuurlijk de “triviale” oplossing die een volledig lege, vlakke ruimtetijd beschrijft.) Inmiddels zijn we honderd jaar verder, en zijn er allerlei andere oplossingen bekend. Daar zijn ook  oplossingen bij die meer gecompliceerde zwarte gaten beschrijven, zoals de Reissner-Nordström-oplossing (gevonden door de Duitser Hans Reissner en de Fin Gunnar Nordström in 1918) die een zwart gat met elektromagnetische lading beschrijft, en de pas veel later ontdekte Kerr-oplossing (gevonden door de Nieuw-Zeelander Roy Kerr in 1963) die een roterend zwart gat beschrijft.

Naar boven

De singulariteit

Een vraag die na de bovenstaande beschrijving voor de hand ligt, is: waar blijft alle ruimte die in het zwarte gat gezogen wordt? Een plaatje dat de situatie schetsmatig weergeeft is te zien in afbeelding 4. Hier is te zien hoe de ruimte binnen het zwarte gat wordt samengezogen in een soort slurf, die in het Engels ook wel de throat (keel) van het zwarte gat wordt genoemd. In zekere zin is dit plaatje echter ook misleidend: hoewel de “put” in het zwarte gat in deze weergave oneindig diep lijkt, wordt de ruimte ook steeds meer versneld, en bereikt een materiedeeltje dat met de ruimte mee het zwarte gat in wordt gezogen toch in een bepaalde eindige hoeveelheid tijd de bodem van de put. Wat er precies op die bodem gebeurt, wordt echter niet voorspeld door de relativiteitstheorie. In de relativistische beschrijving houdt de ruimtetijd daar gewoon op in een punt waar alle materie uiteindelijk naartoe valt. Het moge duidelijk zijn dat dit geen erg bevredigende beschrijving is: in dat ene punt zou zich dan alle massa die ooit in het zwarte gat gevallen is, moeten bevinden. Het punt zou dus bijvoorbeeld een oneindig hoge dichtheid moeten hebben! Dit bevreemdende punt wordt ook wel de singulariteit van het zwarte gat genoemd.

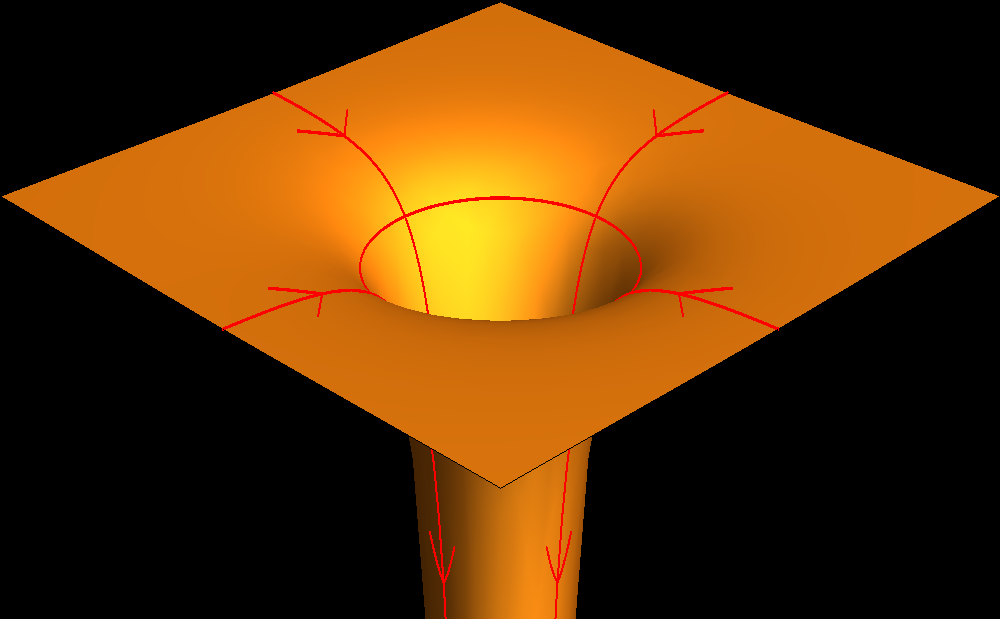
Afbeelding 4. Een zwart gat.Het gele oppervlak is een tweedimensionaal model van de ruimte rond een driedimensionaal zwart gat. De ruimte wordt met steeds grotere snelheid een diepe “put” in gezogen. Op de plek van de rode cirkel is die snelheid precies de lichtsnelheid: dit is de horizon van het zwarte gat, waarvan de straal gelijk is aan de Schwarzschildstraal. De put is oneindig diep, maar de steeds versnellende invallende materie bereikt toch in een eindige hoeveelheid tijd de bodem. Wat zich precies afspeelt in de singulariteit die zich daar bevindt, is vooralsnog een onbeantwoorde natuurkundige vraag.

De beschrijving van het “middelpunt” van een zwart gat als singulariteit lijkt niet erg fysisch, en dat is ook niet zo verwonderlijk. We weten immers dat de relativiteitstheorie op extreem kleine schaal en bij extreem hoge materiedichtheid de natuur niet perfect beschrijft. Op die schaal hebben we ook de quantummechanica nodig om de natuur goed te kunnen beschrijven. De singulariteit van een zwart gat is dus precies een plek die we alleen goed kunnen beschrijven in een theorie waarin zowel de relativiteitstheorie als de quantummechanica een rol speelt. Helaas voor ons is zo’n theorie op dit moment nog niet bekend – zie het artikel over quantumzwaartekracht dat eerder op deze website verscheen.

Voorlopig laten we de vraag wat er zich binnen in het zwarte gat afspeelt dus even achter ons. De precieze beschrijving van de singulariteit blijkt echter lang niet het enige mysterieuze vraagstuk rond zwarte gaten te zijn. Ook in de buurt van de horizon spelen zich allerlei zaken af die we nog niet goed begrijpen, en ook daar blijken de quantummechanica en de relativiteitstheorie een belangrijke rol te spelen. Hoewel ook die vragen nog lang niet naar volle tevredenheid van natuurkundigen beantwoord zijn, hebben we in de afgelopen decennia wel veel meer geleerd over de zaken die zich op de rand van een zwart gat afspelen. Vanaf het volgende artikel gaan we daarom dieper in op de quantum-beschrijving van zwarte gaten. We beginnen die beschrijving met een beroemde ontdekking die de bekende natuurkundige Stephen Hawking in de jaren ’70 deed.

Naar boven

In het vierde artikel van het dossier over zwarte gaten bespreken we de Hawkingstraling van zwarte gaten.