Zwarte gaten (8): Complementariteit

In dit artikel:

• Reflectie?
• Quantumklonen?
• Complementariteit
• Een oplossing… of toch niet?

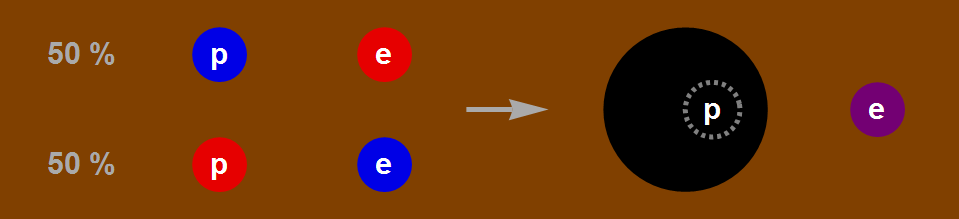
Afbeelding 1. Een grafische weergave van de informatieparadox.Links een deeltjespaar bestaande uit een positron (p) en een elektron (e). Het paar is in een superpositie van toestanden: het is voor 50% in de toestand “positron spin up (blauw), elektron spin down (rood)”, en voor 50% in de tegengestelde toestand. Deze gegevens vormen samen de volledige informatie over het quantumsysteem. Rechts is het positron in een zwart gat verdwenen. Daarmee hebben we geen volledige informatie meer over het systeem: de spin van het positron zou binnenin het zwarte gat gemeten kunnen worden, maar we kunnen dat buiten het zwarte gat nooit ontdekken. In dit geval is er nog altijd een kans van 50% op elk van de mogelijke meetuitkomsten voor de spin van het elektron (aangegeven door de paarse kleur – het “gemiddelde” van rood en blauw), maar deze kansen zijn nu een gevolg van onze onwetendheid. Tenzij we de informatie over het positron weer aan het zwarte gat kunnen ontfutselen, lijkt er dus informatie verloren te gaan – iets wat in tegenspraak is met de grondbeginselen van de quantummechanica.

Reflectie?

De grote vraag voor theoretisch natuurkundigen is dus: zou het kunnen dat we zwarte gaten toch niet helemaal goed begrijpen, en dat op de een of andere manier de informatie over het invallende positron wel te achterhalen valt? Laten we om te beginnen een heel naïeve suggestie voor een antwoord op deze vraag bekijken. We zullen snel zien dat deze suggestie veel té naïef is, maar we blijken er wel door op het spoor van meer realistische oplossingen gezet te worden.

De naïeve suggestie waar we het over hebben, is de volgende. Zou het kunnen dat het positron (of in elk geval de informatie over dat deeltje) helemaal niet in het zwarte gat verdwijnt, maar dat het deeltje op de een of andere manier – voordat het de horizon passeert – gereflecteerd wordt en het zwarte gat dus weer uit beweegt?

Dit lijkt een bizarre suggestie, maar er is in elk geval één goed argument voor het idee te geven. Zoals we in het dossier over relativiteitstheorie hebben gezien, gebeuren er in extreem relativistische situaties allerlei bijzondere dingen met ruimte en tijd. Uit de speciale relativiteitstheorie kennen we voorbeelden waarin heel snel bewegende waarnemers meetlatten korter zien worden (lorentzcontractie) of klokken langzamer zien lopen (tijdsdilatatie). Ook in de algemene relativiteitstheorie komen dergelijke verschijnselen voor – in dat geval in heel sterke zwaartekrachtsvelden. Ook klokken die zich in zo’n zwaartekrachtsveld bevinden, zal een waarnemer van veraf bijvoorbeeld veel langzamer zien lopen. Dit effect is bij een zwart gat zelfs zo sterk dat een waarnemer die ver weg staat de tijd vlak bij een zwart gat vrijwel stil ziet staan!

Afbeelding 2. The Persistence of Memory.In zijn beroemde schilderij ‘The Persistence of Memory’ wil Salvador Dalí de bijzondere manier weergeven waarop verschillende waarnemers volgens de relativiteitstheorie ruimte en tijd waarnemen. Het origineel van dit schilderij is te zien in het Museum of Modern Art in New York.

Dit ‘vertragen’ van de tijd op de rand van een zwart gat heeft een heel belangrijk gevolg. Wie van veraf kijkt naar een deeltje dat in een zwart gat valt, zal dat deeltje vreemd genoeg dus steeds langzamer naar het zwarte gat toe zien vallen naarmate het dichter bij het zwarte gat komt. Sterker nog: de waarnemer op grote afstand zal het deeltje nooit de horizon zien passeren! Het deeltje zal steeds dichter en dichter bij de horizon lijken te komen, maar doet dat steeds langzamer en langzamer, waardoor het het laatste kleine stukje nooit helemaal lijkt af te leggen. Van veraf gezien lijken we daardoor rondom een zwart gat een soort ‘schil’ net buiten de horizon te zien waarop alle invallende materie ‘vastgeplakt’ zit.

Vanuit dat oogpunt bekeken, is ons naïeve voorstel dus niet zo heel vreemd. Zou het misschien kunnen dat het positron, dat vanuit een waarnemer op afstand gezien toch nooit de horizon passeert, op de een of andere manier de informatie over zijn toestand weer naar buiten reflecteert als we met alle quantummechanische en relativistische effecten rekening houden?

Als we wat verder over deze suggestie nadenken, stuiten we echter al snel op een probleem. We hebben de situatie hierboven vanuit een heel specifieke waarnemer beschreven: een waarnemer die zich op heel grote afstand van het zwarte gat bevindt. Voor zo’n waarnemer lijkt de tijd op de rand van het zwarte gat vrijwel stil te staan, maar dat is beslist niet voor elke waarnemer het geval! Hoe zou ons gedachte-experiment eruitzien voor een waarnemer die met het positron mee het zwarte gat in valt?

Het antwoord is: voor een dergelijke waarnemer zou er op de horizon van het zwarte gat waarschijnlijk heel weinig bijzonders gebeuren. De horizon van een zwart gat is volgens de algemene relativiteitstheorie namelijk van dichtbij gezien helemaal geen bijzondere plaats: een waarnemer die door zo’n horizon naar binnen valt, ziet op die plek helemaal niets speciaals. De ruimte in de buurt van de horizon ziet er lokaal precies hetzelfde uit als elk ander stuk ruimte, en de klok van de vallende waarnemer tikt voor hemzelf natuurlijk gewoon met één seconde per seconde. Kortom: vanuit de met het positron meevallende waarnemer gezien, is er op het eerste gezicht geen enkele reden om aan te nemen dat er op de horizon iets met het positron gebeurt, en dus ook niet om aan te nemen dat precies op dat punt (of in de buurt van dat punt) de informatie over het deeltje weer naar buiten toe gereflecteerd wordt.

Naar boven

Quantumklonen?

Toch brengt bovenstaande ‘nep-oplossing’ ons iets dichter bij een veel interessantere mogelijke oplossing. Een waarnemer die in vrije val een zwart gat in valt, wordt ook wel een invallende waarnemer genoemd. Vanuit zo’n invallende waarnemer gezien, lijkt er niets bijzonders te gebeuren, en zou het dus heel logisch zijn als de informatie over het positron uiteindelijk achter de horizon in het zwarte gat belandt. Aan de andere kant: vanuit de ver weg staande waarnemer gezien, verwachten we dat de informatie op de een of andere manier terug naar buiten komt, zodat de informatieparadox wordt vermeden.

Zou het misschien kunnen dat op de een of andere manier allebei deze dingen gebeuren? Zou het kunnen dat de informatie zowel in het zwarte gat verdwijnt als weer naar buiten komt? Ook deze gedachtesprong lijkt in eerste instantie veelbelovend. We kennen in het dagelijks leven genoeg situaties waarin informatie op verschillende plaatsen tegelijk belandt. Als ik een e-mail naar persoon A stuur met een cc naar persoon B, arriveert de informatie die ik verstuurd heb uiteindelijk op twee verschillende plaatsen. Als ik een brief een aantal maal kopieer en vervolgens verstuur, verspreid ik ook dezelfde informatie over verschillende eindbestemmingen.

Afbeelding 3. Dolly.Dolly, het beroemde gekloonde schaap. Hoewel het klonen van een schaap mogelijk is, blijkt het klonen van een quantumtoestand dat niet te zijn. Foto: Toni Barros.

Zou het kunnen dat een zwart gat ook op de één of andere manier als ‘kopieerapparaat’ werkt, en dat dus uiteindelijk één kopie van de informatie achter de horizon het zwarte gat in verdwijnt, en een andere kopie weer naar buiten komt zodat ook de waarnemer op grote afstand de informatie kan achterhalen?

Helaas lijkt bij nadere beschouwing ook deze constructie niet te werken. De reden daarvoor volgt uit een grondige studie van het wiskundige formalisme achter de quantummechanica. Het blijkt in die theorie onmogelijk te zijn om een volledige quantumtoestand te kopiëren. Het maken van een kopie is namelijk niet mogelijk zonder de oorspronkelijke toestand enigszins te beïnvloeden, net zoals het maken van een fotokopie niet mogelijk is zonder licht op het origineel te laten vallen en daarmee het origineel enigszins te beïnvloeden. Die invloed is op een macroscopisch vel papier natuurlijk niet zo heel groot, maar op een microscopische quantumtoestand veel groter. Het blijkt mogelijk te zijn om uit te rekenen dat voor het maken van een exacte kopie van een quantumtoestand, die toestand zodanig sterk beïnvloed wordt dat we alle informatie over het oorspronkelijke systeem verliezen. Dit heet in de quantumfysica het no cloning theorem: het is niet mogelijk om een ‘kloon’ van een quantumtoestand te maken en tegelijkertijd de oorspronkelijke toestand te bewaren. Ook de suggestie van het zwarte gat als ‘kopieerapparaat’ lijkt hier dus spaak te lopen.

Naar boven

Complementariteit

Toch zijn we nu nog maar één denkstap verwijderd van een veel serieuzere poging om de informatieparadox op te lossen. Die laatste denkstap maakt gebruik van een belangrijk feit uit de relativiteitstheorie: verschillende waarnemers kunnen dezelfde situatie op verschillende manieren ervaren. Denk bijvoorbeeld aan het begrip gelijktijdigheid. Het is een bekend verschijnsel uit de relativiteitstheorie dat twee gebeurtenissen die voor de ene waarnemer gelijktijdig lijken te zijn, voor een andere waarnemer op twee totaal verschillende tijdstippen kunnen plaatsvinden.

Kortom: het is in de relativiteitstheorie helemaal niet nodig – en vaak zelfs niet mogelijk – om een fysische situatie op een unieke, waarnemeronafhankelijke manier te beschrijven. Twee waarnemers kunnen dezelfde situatie vaak prima op andere manieren ervaren, zolang er (a) geen vreemde dingen gebeuren die oorzaken en gevolgen omdraaien, en (b) voor elke waarnemer de situatie aan dezelfde natuurwetten voldoet.

Dit moet dus in het bijzonder gelden voor ons tweetal waarnemers hierboven – de waarnemer ver buiten het zwarte gat, en de waarnemer die met het positron mee het zwarte gat in valt. Zolang er voor elk van deze waarnemers afzonderlijk maar één kopie van de informatie over het positron bestaat, is er geen probleem met het ‘no cloning theorem’.

Afbeelding 4. De konijn-eendillusie.In deze beroemde illusie kunnen verschillende personen dezelfde afbeelding op een heel andere manier interpreteren. De ene waarnemer ziet een eend met de bek naar links, de andere ziet een konijn met de oren naar links. Dit geeft het idee van complementariteit goed weer: twee verschillende waarnemers kunnen dezelfde situatie op geheel verschillende manieren interpreteren, zonder dat er een tegenspraak is. De oorspronkelijke afbeelding verscheen in 1892 in het Duitse tijdschrift ‘Fliegende Blätter’. De tekenaar is onbekend.

Deze gedachtegang leidde de Nederlandse Nobelprijswinnaar Gerard ’t Hooft in de jaren ’80 tot een idee dat begin jaren ’90 door de fysici Laurus Thorlacius en Leonard Susskind verder werd uitgewerkt, en dat sindsdien bekend staat onder de naam complementariteit. Het idee van ’t Hooft, Susskind en Thorlacius was als volgt: misschien is het wel zo dat de invallende waarnemer en de waarnemer ver weg twee totaal verschillende ‘werkelijkheden’ zien. De invallende waarnemer ziet de informatie over het zwarte gat met het positron mee naar binnen verdwijnen. De buitenstaande waarnemer ziet de informatie gereflecteerd worden, en ziet dus volgens het ‘no cloning theorem’ hooguit een volledig verstoorde en informatieloze kopie met de invallende waarnemer mee het zwarte gat in vallen.

Dit idee lijkt volledig in tegenspraak met onze twee voorwaarden hierboven: dat twee waarnemers alleen verschillende waarnemingen aan een systeem kunnen doen als dat de causaliteit en de natuurwetten niet schendt. In dit geval lijkt er een groot probleem met causaliteit te ontstaan zodra de invallende waarnemer aan de buitenstaande waarnemer vertelt hoe hij de toestand van het positron ziet. Volgens zijn eigen perspectief zou daar namelijk helemaal niets aan moeten veranderen bij het passeren van de horizon, terwijl volgens de buitenstaande waarnemer die toestand volledig verstoord zou moeten worden. Maar nu komt de crux van het idee: de invallende waarnemer kan helemaal niet met de buitenstaande waarnemer praten! Hij verdwijnt immers op het moment dat de twee beschrijvingen met elkaar in tegenspraak komen achter de horizon, en kan vanaf dat moment geen signalen meer het zwarte gat uit zenden. Met andere woorden: er zijn op dat moment twee ‘complementaire werelden’ die niet meer in causaal contact met elkaar zijn: de wereld van de invallende waarnemer, waarin de informatie met hem mee naar binnen verdwijnt, en de wereld van de buitenstaande waarnemer, waarin de informatie naar buiten terugkomt. Doordat er geen contact tussen deze twee werelden mogelijk is, is er op fundamenteel niveau geen tegenspraak met de relativiteitstheorie of de quantummechanica.

Naar boven

Een oplossing… of toch niet?

Deze oplossing voor de informatieparadox lijkt rechtstreeks afkomstig uit een science-fictionboek. Het idee dat twee waarnemers twee totaal verschillende, complementaire werelden zouden zien, is niet iets dat we uit andere natuurverschijnselen kennen. Het lijkt een heel erge ad-hoc oplossing voor het probleem. Toch bleek bij nadere bestudering dat het heel lastig was om argumenten tegen deze oplossing te verzinnen. Juist doordat de twee waarnemers nooit meer met elkaar in contact kunnen komen, lijkt de verrassende redenering van complementariteit waterdicht te zijn.

Sinds de jaren ’90 werd complementariteit daarom lange tijd gezien als een serieuze kandidaat om de informatieparadox op te lossen. De vraag leek vooral te zijn hoe men zou kunnen aantonen dat dit de juiste oplossing was. Alleen het feit dat de oplossing geen interne tegenspraken lijkt te vertonen, is natuurlijk lang niet voldoende om die ook als waarheid aan te nemen!

Enkele jaren geleden begon echter de twijfel over het idee van complementariteit toch weer toe te nemen. Directe aanleiding daarvoor was het verschijnen van een artikel van de natuurkundigen Ahmed Almheiri, Donald Marolf, Joe Polchinski en James Sully in 2012. In dat artikel werd aangetoond dat het idee van complementariteit toch niet zo vrij van problemen is als men sinds de vroege jaren ’90 had gedacht. Wat het probleem precies is, en welke nieuwe ideeën over de informatieparadox dit opleverde, beschrijven we in het volgende artikel. Centraal hierin staat een begrip dat de afgelopen jaren veel in het populairwetenschappelijke nieuws is geweest: dat van de black hole firewall.

Naar boven

In het negende artikel van deze serie bespreken we de firewall-paradox.