Relativiteit (11): Gekromde ruimtetijd

Laten we nog eens iets beter kijken naar het voorbeeld met de twee liften uit het vorige artikel. We boren nu een klein gat in de rechterzijkant van de liften, en laten een foton (een lichtdeeltje) dat eenparig van rechts naar links beweegt door dit gat naar binnen vallen. Hoe nemen de waarnemers in de liften deze invallende lichtstraal waar?

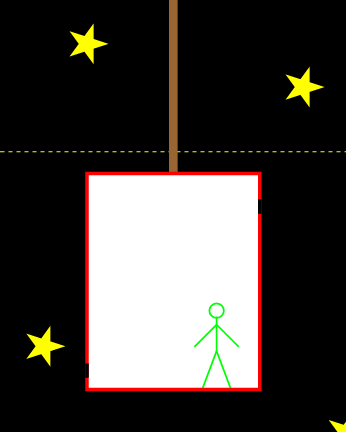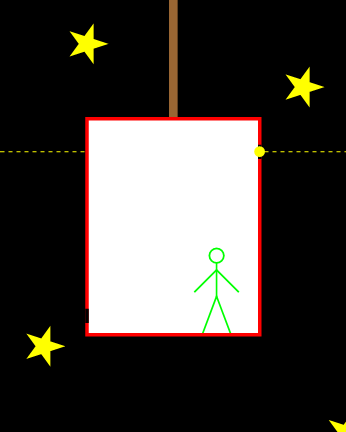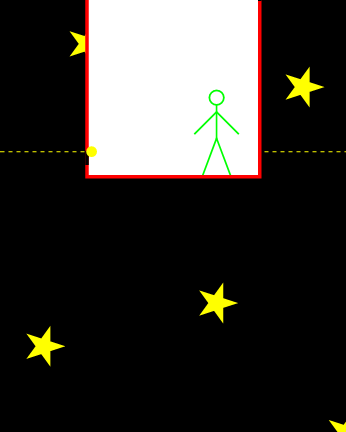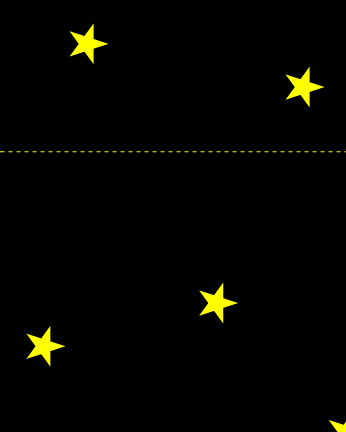
Afbeelding 1. Een foton in een lift.Een waarnemer in een versnellende lift ziet een lichtdeeltje van rechts naar links door de lift bewegen.

We bekijken de situatie allereerst vanuit de versnellende lift in de ruimte – zie afbeelding 1. Terwijl het foton van rechts naar links beweegt, versnelt de lift omhoog. (De versnelling ten opzichte van de snelheid van het lichtdeeltje is hier voor de duidelijkheid overdreven groot gekozen.) De waarnemer in de lift ziet het foton dus de linkerkant van de lift bereiken in een punt dat lager ligt dan het gat in de rechterkant. Dezelfde situatie vanuit het perspectief van de waarnemer is getekend in afbeelding 2. Het lijkt voor de versnellende waarnemer alsof de lichtstraal in een kromme baan (om precies te zijn: een paraboolbaan) omlaag beweegt. Het licht lijkt voor hem dus “omlaag te vallen”.

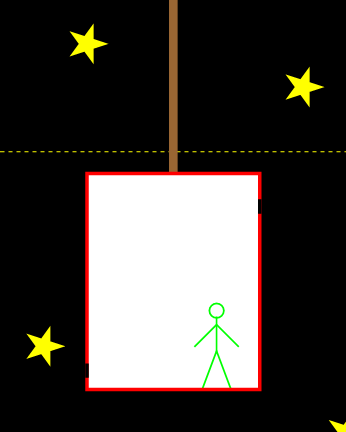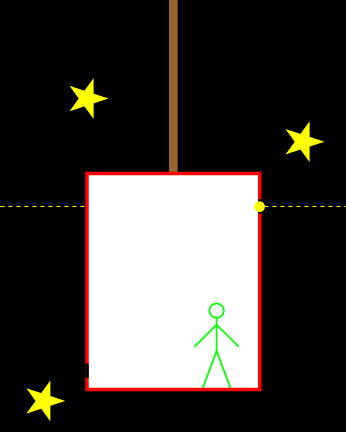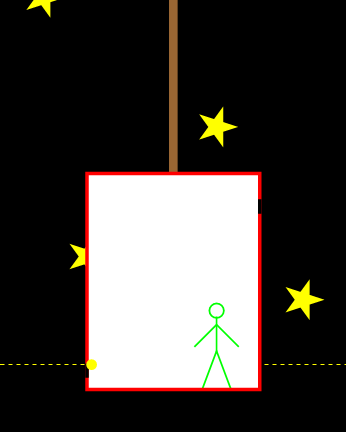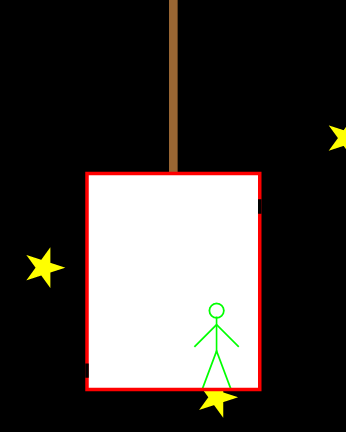
Afbeelding 2. Een foton in een lift.Dezelfde situatie als in afbeelding 1, maar nu gezien vanuit de versnelde waarnemer. Het licht lijkt voor hem in een paraboolbaan te bewegen.

Uit het equivalentieprincipe volgt nu dat de waarnemer in de lift op aarde precies hetzelfde moet ervaren. Met andere woorden: ook in zijn lift beweegt het licht volgens een gekromde baan – zie afbeelding 3. Het lijkt voor deze waarnemer dus alsof het licht door de zwaartekracht van de aarde wordt aangetrokken!

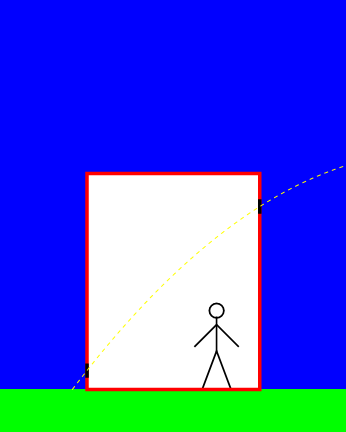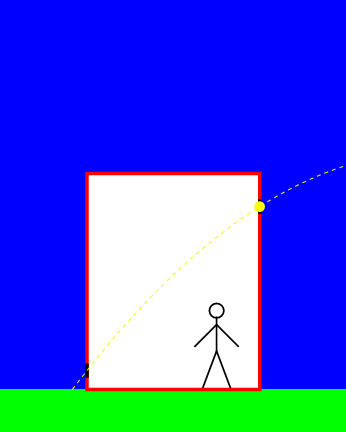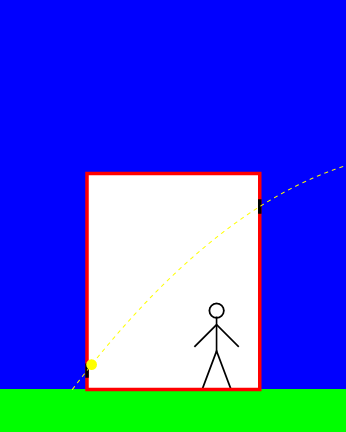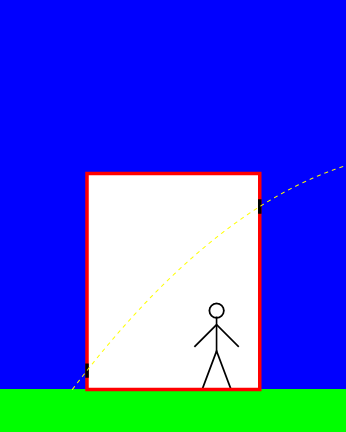
Afbeelding 3. Een foton in een zwaartekrachtsveld.Een waarnemer in een stilstaande lift op aarde ziet een foton van rechts naar links door de lift bewegen. Volgens het equivalentieprincipe moet hij het licht in dezelfde paraboolbaan zien bewegen als de versnelde waarnemer in afbeelding 2.

In het klassieke wereldbeeld is dit een erg vreemde conclusie. Licht heeft immers geen massa, en volgens de zwaartekrachtswet van Newton worden alleen objecten met massa door de zwaartekracht aangetrokken. In Newtons wereldbeeld zouden we dus verwachten dat het licht in een zwaartekrachtsveld gewoon rechtdoor beweegt.

Dit verschil tussen het equivalentieprincipe en de zwaartekrachtswet van Newton gebruikte Einstein als basis voor zijn algemene relativiteitstheorie. Hij redeneerde als volgt: als zelfs licht in een zwaartekrachtsveld een gekromde baan beschrijft, is zwaartekracht dus niet precies een kracht die op mysterieuze wijze aan massa’s trekt. Het is veel meer alsof de ruimte – of beter: de ruimtetijd – zelf krom is, zodat alles wat erdoorheen beweegt in kromme banen voortbeweegt.

Dit idee werd de kiem voor de algemene relativiteitstheorie. Einstein zei: zwaartekracht is uiteindelijk niets anders dan gekromde ruimtetijd. Massa’s, zoals de aarde, krommen de ruimtetijd om zich heen, waardoor andere objecten in gekromde banen bewegen en dus naar de massa’s toe lijken te vallen. Plaatselijk volgen die objecten een “zo recht mogelijke baan” (een zogenaamde geodeet), maar uiteindelijk bewegen ze door de kromming van de ruimtetijd toch in gekromde banen.

Laten we om dit beter te begrijpen eens kijken naar een voorbeeld waarin we alleen de ruimte krommen, bijvoorbeeld door het gekromde oppervlak van de aarde te bestuderen – zie afbeelding 4. Twee waarnemers bevinden zich op verschillende plaatsen op de evenaar, op zo’n 3.000 kilometer van elkaar af. De waarnemers spreken af om vanaf hun locatie allebei recht naar het noorden te vliegen. Ze beginnen dus in parallelle richtingen te bewegen, en volgen daarbij zo goed mogelijk een rechte baan over het aardoppervlak. Toch zullen de waarnemers uiteindelijk merken dat ze steeds dichter naar elkaar toe bewegen, en uiteindelijk zelfs in hetzelfde punt (de Noordpool) uitkomen. Het is alsof de twee waarnemers elkaar aantrekken!

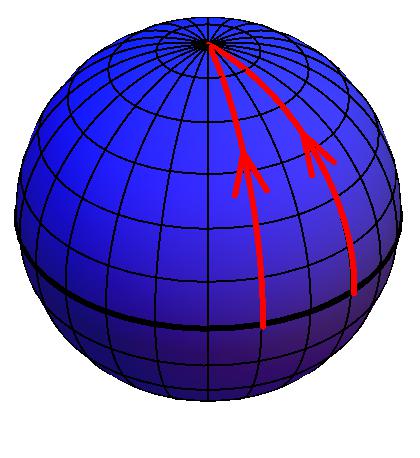
Afbeelding 4. Geodeten op aarde.In een gekromde tweedimensionale ruimte, zoals op het aardoppervlak, kunnen trajecten die oorspronkelijk parallel lopen, elkaar na enige tijd toch naderen.

Precies hetzelfde gebeurt in de gekromde ruimtetijd met zware massa’s. Als we twee zware massa’s (bijvoorbeeld planeten) in parallelle banen de ruimte in schieten zullen ze oorspronkelijk in parallelle richtingen blijven bewegen, maar uiteindelijk langzaam (en op den duur steeds sneller) naar elkaar toegetrokken worden. Onze klassieke beschrijving van dit verschijnsel is dat de twee massa’s elkaar met hun onderlinge zwaartekracht aantrekken, maar in Einsteins beschrijving ligt het iets anders: de massa’s krommen de ruimtetijd om zich heen, en door de kromme banen (geodeten) die de massa’s vervolgens volgen, bewegen ze steeds dichter naar elkaar toe.

Einstein wist deze beschrijving van zwaartekracht als gekromde ruimtetijd in een aantal elegante wiskundige formules te vangen, en kon aantonen dat op grote schaal deze zwaartekrachtswetten tot vrijwel exact dezelfde resultaten leiden als de oude wetten van Newton. Er zijn echter minieme afwijkingen – net zoals er in de speciale relativiteitstheorie heel kleine afwijkingen zijn ten opzichte van de klassieke bewegingswetten – afwijkingen die we in dagelijkse omstandigheden nauwelijks ervaren. De vraag was dus: konden deze kleine afwijken waargenomen worden, zodat ook de algemene relativiteitstheorie getest kon worden?

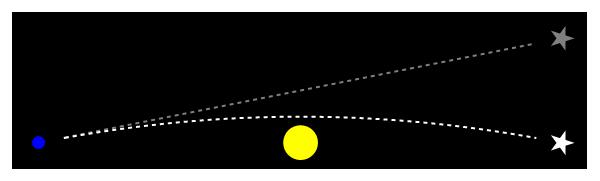
Afbeelding 5. Afbuiging van sterlicht.Het licht van een ster (wit) wordt door de zon (geel) afgebogen in de richting van de aarde (blauw). Door de aanwezigheid van de zon zien we het licht uit een andere richting aankomen dan normaal het geval is. De ster lijkt dus op de plek te staan die in het grijs is aangegeven.

Een belangrijke test voor de algemene relativiteitstheorie is de vraag of ook licht in een zwaartekrachtsveld afgebogen wordt. Zoals we zagen is dit immers volgens de theorie van Newton niet het geval, maar volgens die van Einstein wel. Al snel na het publiceren van de relativiteitstheorie werd daarom geprobeerd deze buiging van het licht waar te nemen. De eenvoudigste manier om dit te doen is tijdens een totale zonsverduistering: dan kunnen we vlak naast de zon (die is afgedekt door de vrijwel even grote maanschijf) sterren zien staan, waarvan het licht dus ook vlak langs de zon is gescheerd. Als de algemene relativiteitstheorie klopt, moet dit licht door de zon zijn afgebogen, en moeten we de sterren dus in een iets andere richting zien dan waar ze normaal staan – zie afbeelding 5. Uiteindelijk lukte het Arthur Eddington in 1919 om deze afbuiging van het sterlicht tijdens een expeditie naar Afrika ook daadwerkelijk waar te nemen. Overigens ontstond er later de nodige ophef over de vraag of Eddingtons metingen wel nauwkeurig genoeg waren. Een heranalyse uit 1979 toonde aan dat Eddington inderdaad voldoende nauwkeurige data had om het voorspelde effect te kunnen meten. Hoe het ook zij, in de jaren die volgden werd het experiment nog de nodige keren herhaald, en inmiddels hebben we met grote precisie kunnen vaststellen dat het zonlicht inderdaad wordt afgebogen zoals de relativiteitstheorie voorspelt. Tegenwoordig zien we ditzelfde effect ook op veel grotere schaal aan de sterrenhemel: wanneer een nabij sterrenstelsel precies op één lijn staat met een verder weg gelegen stelsel wordt het licht van deze laatste door de eerste afgebogen. Het licht kan zelfs aan alle kanten rond het voorste sterrenstelsel gebogen worden, waardoor we aan meerdere kanten van het voorste stelsel hetzelfde achterste stelsel zien staan – of waardoor het laatste zelfs in een ring om het eerste heen “geprojecteerd” wordt. Een dergelijk verschijnsel – zie afbeelding 6 -word een gravitatielens genoemd.

Afbeelding 6. Een gravitatielens.Het voorste (gele) sterrenstelsel buigt het licht van een achterliggend (wit) sterrenstelsel af, zodat een ringvormig beeld rond het voorste stelsel wordt gevormd. (Foto: NASA, Hubble Space Telescope.)

Na de eerste experimentele verificatie van de algemene relativiteitstheorie volgden nog vele andere. Een andere leuke test is bijvoorbeeld de volgende. Volgens de wetten van Newton bewegen planeten in onveranderlijke ellipsbanen rond de zon. Als we de wetten van Einstein toepassen, zien we echter dat de banen zogenaamde periheliumprecessie vertonen: de ellipsen waarlangs ze bewegen, schuiven langzaam op – zie afbeelding 7. Hoe dichter de planeet bij de zon staat, hoe groter dit effect is, en in het bijzonder is het dus interessant om te zien of we dit effect kunnen waarnemen bij de binnenste planeet in het zonnestelsel, Mercurius. Dat kan inderdaad. Sterker nog: de periheliumprecessie van Mercurius was al ruim vóór het bedenken van de relativiteitstheorie opgevallen: de Franse wiskundige Urbain Le Verrier merkte het verschijnsel al in 1859 op. Met de komst van de algemene relativiteitstheorie kon dit verschijnsel verklaard worden, en de grootte van de precessie bleek inderdaad precies te kloppen met de voorspelling (of eigenlijk: “naspelling”) van de theorie.

Ook in een bekende moderne technologie, de positiebepaling met behulp van een GPS, speelt de algemene relativiteitstheorie een rol. De GPS in een auto bepaalt zijn positie door signalen op te vangen die van diverse satellieten afkomstig zijn. In deze signalen zenden de satellieten het tijdstip van verzenden en hun precieze locatie mee. De GPS meet wanneer de signalen aankomen, berekent daaruit hoe lang de signalen onderweg zijn geweest, berekent daaruit de afstand tot de satellieten, en daaruit vervolgens weer zijn exacte positie. Voor het omrekenen van de reistijd van het signaal in de afstand tot de satelliet moet echter precies de kromming van de ruimtetijd in aanmerking worden genomen; als de GPS dit niet zou doen en zou aannemen dat de ruimtetijd vlak is, zou het antwoord tot enkele tientallen meters van het juiste kunnen afwijken. Het feit dat de GPS in onze auto’s werkt is dus een prachtige bevestiging van de juistheid van Einsteins theorie!

Afbeelding 7. Periheliumprecessie.De periheliumprecessie van de planeet Mercurius (niet op schaal). Volgens de klassieke mechanica zou de planeet in een vaste ellipsbaan (de witte doorgetrokken lijn) rond de zon (de gele schijf) moeten bewegen. Volgens de relativiteitstheorie schuift de lange as van deze ellips echter langzaam op, wat de gestippelde baan tot gevolg heeft.

Hiermee zijn we aangekomen op een punt waarop we zowel  de speciale als de algemene relativiteitstheorie beschreven hebben. In het volgende en voorlopig laatste artikel van dit dossier bekijken we nog één intrigerende toepassing van de algemene relativiteitstheorie: de verschijnselen die zich afspelen rond de mysterieuze objecten die we zwarte gaten noemen.

Dit is het elfde artikel uit het dossier Relativiteitstheorie. In het twaalfde artikel bespreken we de objecten die misschien wel de meest mysterieuze voorspelling van de algemene relativiteitstheorie zijn: zwarte gaten.