Relativiteit (8): De tweelingparadox

De tweelingparadox is een beroemde schijnbare tegenspraak die uit de relativiteitstheorie lijkt te volgen. Centraal in de paradox staat het begrip tijdsdilatatie: het feit dat de klok van een bewegende waarnemer langzamer lijkt te lopen. De vraag komt in feite neer op het volgende: als de klok van een bewegende waarnemer van mij uit gezien langzamer loopt dan mijn klok, en mijn klok loopt vanuit de bewegende waarnemer gezien langzamer dan zijn klok, levert combinatie van die twee eigenschappen dan niet op dat mijn klok langzamer loopt dan zichzelf?

We moeten de paradox iets beter formuleren dan dat, want om klokken te kunnen vergelijken moeten deze klokken natuurlijk wel op dezelfde plaats zijn. We doen daarom het volgende gedachte-experiment. We nemen een tweeling, Frank en Ronald, en sturen één helft van de tweeling, Ronald, op een lange ruimtereis. Allereerst reist Ronald lange tijd met bijna de lichtsnelheid naar het oosten; vervolgens reist hij even lang met bijna de lichtsnelheid terug naar het westen zodat hij weer bij Frank uitkomt. Is Ronald nu ouder dan Frank, of andersom?

Afbeelding 1. Frank en Ronald de BoerVan een tweeling, Frank en Ronald, maakt Ronald een ruimtereis terwijl Frank op aarde achterblijft. Wie van de twee is jonger als Ronald weer thuiskomt? (Foto: FC Barcelona, 1999)

Doordat Ronald met zo’n enorme snelheid reist, ziet Frank zijn klok veel langzamer lopen dan die van hemzelf. Dit geldt als Ronald van hem af reist, en nog steeds als Ronald weer (met dezelfde snelheid, alleen de andere kant op) naar hem terugreist. Frank ziet de tijd van Ronald dus op elk moment langzamer verstrijken; van Frank uit gezien zou Ronald minder oud moeten zijn geworden als hij thuiskomt dan Frank zelf op dat moment is.

Maar kunnen we precies dezelfde redenering niet vanuit Ronalds gezichtspunt houden? Ook hij ziet Frank eerst met bijna de lichtsnelheid van hem af bewegen, en vervolgens weer met bijna de lichtsnelheid naar hem toe. Volgt daaruit niet dat juist Franks tijd langzamer loopt, en dan Frank dus juist bij terugkomst de jongere broer moet zijn?

De oplossing van de paradox is dat de situatie weliswaar volkomen symmetrisch lijkt tussen de twee broers, maar dat niet is. We moeten goed beseffen dat we het tot nu toe alleen maar over eenparig bewegende waarnemers hebben gehad: waarnemers die met een vaste snelheid door de ruimtetijd bewegen. Voor al deze waarnemers, zo zegt het relativiteitsbeginsel, moeten alle natuurwetten hetzelfde zijn. We hebben het echter nog niet over versnelde waarnemers gehad, en hebben dus ook niet beweerd dat voor waarnemers die versnellen de natuurwetten hetzelfde zijn als voor waarnemers die niet versnellen. En hierin zit hem het verschil waarmee de symmetrie doorbroken wordt: om terug te keren naar Frank moet Ronald halverwege zijn reis zijn raket enorm versnellen (of eigenlijk: afremmen en dan versnellen in tegengestelde richting); iets wat Frank natuurlijk niet doet. Ronald zal dit ook zeker voelen op het moment dat hij omkeert: het afremmen en versnellen leidt tot een schijnkracht die je bijvoorbeeld ook voelt als je in een auto zit die snel wegrijdt, waardoor je hard in je stoel gedrukt wordt. Frank ervaart zo’n versnelling niet, en daaruit blijkt dat de situatie niet volkomen symmetrisch is voor de twee waarnemers. Er is dus niet de mogelijkheid om de rollen te verwisselen en voor Ronald precies dezelfde redenering te gebruiken die we uit het gezichtspunt van Frank – die nooit versnelt – konden gebruiken.

Wat gebeurt er dan precies vanuit Ronalds gezichtspunt op het moment dat hij omdraait? Dit zien we in afbeelding 2. De dikke rode lijn is de wereldlijn van Ronald. Zolang Ronald naar rechts beweegt, is de steile groene lijn zijn tijdlijn, en de vlakke groene lijn een van zijn ruimtelijnen – degene waarop onder andere de gebeurtenis “Ronald keert om” ligt. Alle gebeurtenissen op deze lijn zijn op dat moment dus gelijktijdig voor Ronald. In het bijzonder geldt dat voor de onderste rode stip in het diagram, die zich op de wereldlijn van Frank bevindt.

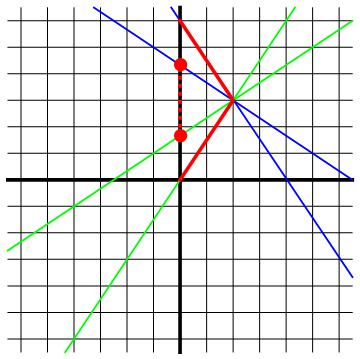
Afbeelding 2. De oplossing van de tweelingparadox.De rode lijn geeft de wereldlijn van Ronald weer. Vlak voor hij omkeert zijn de gebeurtenissen op de vlakke groene lijn (en dus in het bijzonder de onderste rode stip) gelijktijdig met zijn omkeren. Vlak nadat hij omeert zijn de gebeurtenissen op de vlakke blauwe lijn (en dus in het bijzonder de bovenste rode stip) gelijktijdig met zijn omkeren. Ronald slaat dus als het ware een stuk van Franks geschiedenis over. Hierdoor is Frank als Ronald terugkeert ouder dan hijzelf – en niet jonger, zoals we zouden denken als we vanuit Ronalds oogpunt alleen rekening zouden houden met de tijdsdilatatie.

Zodra Ronald omkeert gebeurt er echter iets extreems. Zijn tijdlijn wordt nu de steile blauwe lijn, en de vlakke blauwe lijn is één van zijn ruimtelijnen, weer die waarop de gebeurtenis “Ronald keert om” ligt. Alle gebeurtenissen op déze lijn zijn nu voor Ronald gelijktijdig, en dus in het bijzonder de gebeurtenis aangegeven met de bovenste rode stip, die op Franks wereldlijn ligt. Ronald slaat dus als het ware in één klap een enorm stuk van Franks leven over – het stuk dat in de afbeelding rood gestippeld is. Hierna zal Franks klok vanuit Ronalds gezichtspunt weer langzamer lopen dan die van hemzelf. Dit “overslaan” van een stuk tijd compenseert ruimschoots voor het langzamer lopen van de klokken, en zorgt ervoor dat Frank inderdaad ouder is dan Ronald, en dus niet jonger, als Ronald terugkomt.

De paradox is hiermee opgelost; Ronald is inderdaad jonger dan Frank als hij terugkeert, en niet andersom. Dit is ook precies wat wordt waargenomen in het experiment met de bewegende klokken van Hafele en Keating, dat we in het artikel over de tijdsdilatatie besproken. De atoomklokken die met de vliegtuigen waren meegestuurd (en die versnellen doordat ze niet in een rechte baan bewegen maar rond de aarde draaien) bleken inderdaad achter te lopen ten opzichte van de atoomklokken die in het laboratorium waren gebleven.

We maken, om verwarring te voorkomen, nog twee aanvullende opmerkingen over het bovenstaande gedachte-experiment:

1. Ronald “slaat een stuk van Franks geschiedenis over” in de zin dat direct nadat de onderste rode stip in afbeelding 2 gelijktijdig is met zijn omkeermoment, opeens de bovenste rode stip gelijktijdig is met dat moment. Dat wil niet zeggen dat hij dit stuk van Franks leven niet kan waarnemen. Het licht van het tussenliggende stuk is immers wel gewoon naar hem op weg. Wanneer we het hebben over “gelijktijdigheid” corrigeren we altijd voor de tijd die het licht erover doet om ons te bereiken. Zo kunnen we het hebben over iets dat zich in ons referentiekader nu in het Andromeda-sterrenstelsel afspeelt, ondanks dat het licht van die gebeurtenis er nog twee miljoen jaar over zal doen om ons te bereiken. Zodra Ronald omkeert, vliegt hij tegen het licht dat van Frank afkomt in. Hij verkleint daarmee zijn afstand tot Frank, en zal daardoor na elke seconde licht tegenkomen dat meer dan een seconde na het vorige licht vanaf Frank is uitgezonden. Ronald ziet als hij terugvliegt Franks film dus versneld afspelen, en haalt op die manier het “gemiste stuk geschiedenis” in.
2. Een instantane versnelling is natuurlijk in de praktijk niet te realiseren: het direct omkeren van Ronald in afbeelding 2 is dus een idealisatie. In de praktijk zal Ronald langzaam afremmen en weer in tegengestelde richting versnellen: zijn tijlijn zal dus geen scherpe knik maken zoals in de afbeelding, maar op de plaats van die knik een afgeronde curve vormen. De groene ruimtelijn van Ronald klapt daardoor ook niet in één keer om naar de rode ruimtelijn, maar zal langzaam draaien tot hij evenwijdig loopt aan de blauwe. In de praktijk zal de ruimtelijn van Ronald het stuk geschiedenis van Frank dus niet overslaan, maar er heel snel “overheen zwaaien”.

Afbeelding 3. De Andromedanevel.Het licht dat wij uit het Andromedasterrenstelsel zien komen, is twee miljoen jaar onderweg geweest. Wanneer we het hebben over “gelijktijdigheid” tellen we deze reistijd niet mee. Gebeurtenissen in ons referentiekader op dit moment in het Andromedastelsel gebeuren, zien we dus pas over twee miljoen jaar. (Foto: Marcel Vonk.)

Ook in dit voorbeeld hebben we weer gezien dat de relativiteitstheorie “tricky business” is: als we onvoorzichtig redeneren, leidt onze dagelijkse intuïtie tot allerlei tegenspraken en paradoxen. Zodra we echter nauwkeuriger naar de situatie kijken en de logica van de relativiteitstheorie volledig volgen, ontdekken we hoe deze paradoxen opgelost kunnen worden.

We hebben het nu al acht artikelen lang over de theorie van Einstein gehad, maar hebben daarbij nog altijd zijn wereldberoemde formule niet genoemd. Het wordt in het volgende artikel dus hoog tijd dat we daar eens verandering in brengen.

Dit is het achtste artikel uit het dossier Relativiteitstheorie. In het negende artikel beschrijven we de formule E=mc², en de snelheidsbeperkingen die uit die formule volgen.