Relativiteit (4): Ruimtetijd

We hebben gezien dat we van gebeurtenissen zowel de plaats als het tijdstip aangeven met een coördinaat. Hoewel ruimte en tijd heel verschillende natuurkundige begrippen zijn, zouden we ons aan de hand van deze eenduidige beschrijving dus kunnen afvragen of het zinvol is om ruimte- en tijdcoördinaten samen te voegen tot één geheel.

Dit is beslist geen wereldschokkend idee: het samenvoegen van ruimte- en tijdcoördinaten tot één geheel is precies wat we doen als we bijvoorbeeld een grafiek tekenen die de verandering van een positie in de tijd weergeeft. In afbeelding 1 zien we zo’n grafiek, die de beweging van een auto over een autoweg van 5km lengte weergeeft. We zien dat de auto oorspronkelijk langzaam rijdt (zijn plaatscoördinaat verandert weinig als de tijdcoördinaat toeneemt), vervolgens versnelt, en daarna enige tijd met een constante snelheid blijft rijden. De auto remt vervolgens af (bijvoorbeeld voor een stoplicht), staat zelfs enige tijd helemaal stil, en versnelt daarna weer tot een andere, hogere constante snelheid.

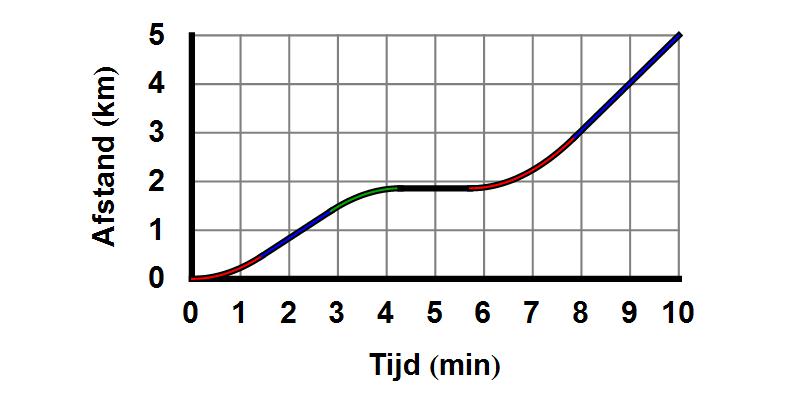
Afbeelding 1. Een tijd-ruimtediagram.De grafliek van een autorit over een weg van 5km. De auto versnelt eerst (rood), rijdt dan met een constante snelheid verder (blauw), vertraagt dan (groen) en staat enige tijd stil (zwart). Vervolgens versnelt de auto weer (rood) en legt tenslotte met een constante snelheid (blauw) de rest van de weg af. Het tweede blauwe segment is steiler dan het eerste; de auto rijdt op dat stuk weg sneller.

We kunnen afbeelding 1 zien als een heel eenvoudig voorbeeld van een ruimtetijd: we hebben een eendimensionale ruimte (de weg) gecombineerd met de tijd, en krijgen zo een tweedimensionaal plaatje. Punten in dit plaatje geven gebeurtenissen weer: het punt waarop het groene lijnstuk in het zwarte overgaat geeft bijvoorbeeld de gebeurtenis “de auto komt stil te staan” aan. Deze gebeurtenis vindt plaats op het punt met coördinaten t=4,2 min, x=1,9 km.

Op dezelfde manier kunnen we natuurlijk allerlei andere grootheden “aan elkaar plakken”. Een grafiek van een beurskoers geeft bijvoorbeeld aan hoe de waarde van een aandeel in de loop van de tijd verandert. De grootheden die we in dit geval samenvoegen tot een tweedimensionaal diagram zijn dus waarde en tijd. Voor een transistor kunnen we de grootheden “stroomsterkte” en “temperatuur” samenvoegen tot een tweedimensionaal diagram, enzovoort. Er lijkt weinig bijzonders aan de hand te zijn met de combinatie “ruimte” en “tijd”. Wat Einstein ontdekte was dat deze combinatie juist wél heel speciaal is, en dat het combineren van ruimte en tijd tot één “ruimtetijd” een fysische betekenis heeft die ver uitstijgt boven het simpelweg tekenen van grafieken.

Laten we voor we de ruimtetijd nader bestuderen nog twee opmerkingen maken.

1. Hoewel we in dit verhaal altijd genoeg zullen hebben aan één ruimtedimensie zijn er in werkelijkheid natuurlijk drie. We moeten de ruimtetijd dus eigenlijk zien als een vierdimensionaal geheel, waarin elk punt wordt beschreven door de vier coördinaten die de plaats en het tijdstip van een gebeurtenis aangeven. Zo’n vierdimensionale ruimtetijd is natuurlijk erg lastig te tekenen – nog een reden waarom het makkelijk is om ons te beperken tot gebeurtenissen en bewegingen in maar één ruimtedimensie.
2. Het is in veel gevallen gebruikelijk om in grafieken de tijdrichting langs de horizontale as te tekenen – dit hebben we bijvoorbeeld ook in afbeelding 1 gedaan. In de relativiteitstheorie is de gewoonte ontstaan om de tijd juist langs de verticale as te zetten. De beweging van de auto wordt in een relativistisch ruimtetijddiagram dus weergegeven als in afbeelding 2 – een gespiegelde versie van afbeelding 1. Deze weergave van grootheden is even wennen (merk bijvoorbeeld op dat hogere snelheden nu overeenkomen met minder steile lijnen in plaats van met steilere lijnen) maar brengt verder weinig problemen met zich mee.

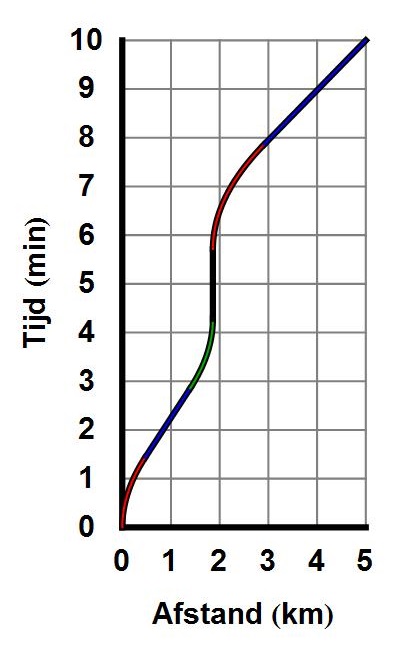
Afbeelding 2. Een ruimtetijddiagram.Hetzelfde diagram als in afbeelding 1, met de ruimte langs de horizontale as en de tijd langs de verticale. In tegenstelling tot afbeelding 1 komt in dit diagram een hogere snelheid overeen met een minder steile lijn.

Het voordeel van het combineren van ruimte en tijd tot één ruimtetijd is dat we eenvoudig grafisch kunnen weergeven hoe Einstein het probleem van de onveranderlijke lichtsnelheid oploste. In afbeelding 3 zien we een heel eenvoudig ruimtetijddiagram dat de beweging van twee lichtflitsen weergeeft – een die naar rechts beweegt, en een die naar links beweegt. Langs de verticale as staat de tijd uitgezet, in seconden. Omdat het licht zo snel gaat, zijn langs de horizontale as nogal extreme eenheden gekozen: één vakje langs de horizontale as komt overeen met 300.000 km (of, preciezer: 299.792.458 m), de afstand die het licht in één seconde aflegt. Die afstand wordt daarom een lichtseconde genoemd. Let op: de naam is misschien wat verwarrend – een lichtseconde is een afstand, en geen tijd! Het gebruik van deze eenheden langs de horizontale as heeft het voordeel dat de weg die het licht aflegt, gegeven wordt door een lijn die precies onder 45 graden ten opzichte van de assen staat. In één tijdseenheid (een seconde) beweegt het licht precies één ruimte-eenheid (een lichtseconde). Een lijn die de baan van een lichtflits of een ander object door de ruimte weergeeft wordt een wereldlijn genoemd.

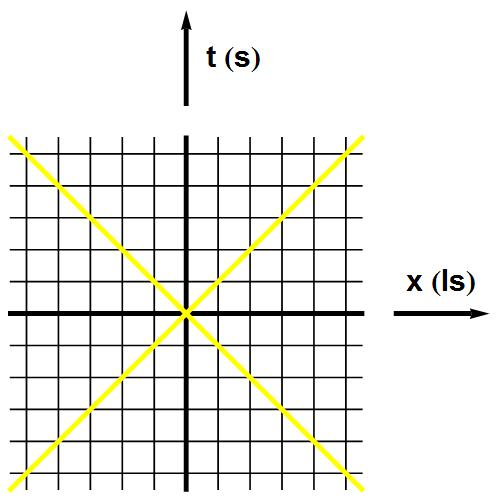
Afbeelding 3. Een eenvoudig ruimtetijddiagram.Langs de horizontale as staat de afstand in lichtseconden uitgezet; langs de verticale as de tijd in seconden. De gele lijnen zijn de wereldlijnen van twee lichtflitsen.

We kunnen afbeelding 3 zien als de beschrijving van de ruimtetijd zoals een bepaalde waarnemer (laten we weer zeggen: de zwarte waarnemer) die zou geven. We voegen nu een tweede, groene waarnemer toe. Deze waarnemer beweegt met een flinke snelheid van een kwart van de lichtsnelheid ten opzichte van de eerste waarnemer naar rechts. In afbeelding 4 hebben we naast de beweging van de lichtflits ook de beweging van de groene waarnemer weergegeven in het ruimtetijddiagram.

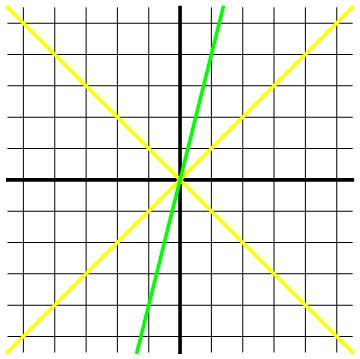
Afbeeldin 4. Een bewegende waarnemer.In het ruimtetijddiagram is nu de groene wereldlijn van een tweede waarnemer toegevoegd. De lijn gaat door het punt (1,4), dus de waarnemer doet 4 seconden over een afstand van 1 lichtseconde. Met andere woorden: hij beweegt met een kwart van de lichtsnelheid.

Merk op dat ook de tweede waarnemer het ontstaan van de lichtflits in zijn oorsprong (x’=0, t’=0) ziet gebeuren: alle waarnemers hebben immers afgesproken dezelfde oorsprong te gebruiken. Verder gebruikt de groene waarnemer een coördinatenstelsel dat met hem meebeweegt: de groene lijn geeft dus niet alleen de achtereenvolgende posities van de groene waarnemer weer, maar ook de gebeurtenissen waaraan hij de coördinaat x’=0 toekent, met verschillende waarden voor de t’-coördinaat. Met andere woorden: we kunnen de groene lijn in afbeelding 4 zien als de t’-as van de tweede waarnemer.

Wat is nu in dit plaatje de x’-as van de groene waarnemer? De x’-as bestaat uit de gebeurtenissen met tijdcoördinaat t’=0 en verschillende x’-coördinaten. In de klassieke natuurkunde is de tijd onafhankelijk van de waarnemer; de gebeurtenissen op t’=0 zijn dus hetzelfde als de gebeurtenissen die de zwarte waarnemer op t=0 ziet plaatsvinden. In de klassieke natuurkunde zouden we de x’-as van de groene waarnemer dus weergeven met de dikke groene gestippelde lijn in afbeelding 5. Omdat tijd absoluut is zijn de x-as en de x’-as precies dezelfde lijnen in de ruimtetijd. Hetzelfde geldt natuurlijk voor gebeurtenissen die op een andere tijd dan t’=0 plaatsvinden: als gebeurtenissen gelijktijdig zijn volgens de ene klassieke waarnemer, zijn ze dat ook volgens de andere. De andere, dun groen gestippelde, horizontale lijnen in afbeelding 5 geven dus andere verzamelingen van gelijktijdige gebeurtenissen weer. We zullen nu zien dat Einstein deze aanname moest opgeven om het relativiteitsbeginsel met de onveranderlijkheid van de lichtsnelheid te verenigen.

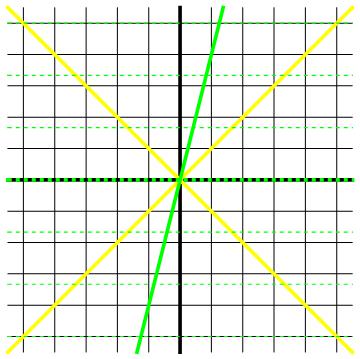
Afbeelding 5. Gelijktijdigheid in het klassieke wereldbeeld.De gestippelde horizontale lijnen geven weer wat volgens de klassieke opvatting in de natuurkunde de ruimtelijnen van de groene waarnemer zijn. Aangezien tijd in die opvatting onafhankelijk is van de waarnemer, zijn de horizontale lijnen (die gebeurtenissen weergeven die op één tijdstip maar op verschillende plaatsen plaatsvinden) voor zowel de zwarte als de groene waarnemer de ruimtelijnen. In het bijzonder hebben beide waarnemers dus dezelfde x-as.

Om te begrijpen hoe de tweede waarnemer in de relativistische ruimtetijd eenzelfde lichtsnelheid kan meten als de eerste, voegen we nog twee groene waarnemers toe, die zich op gelijke afstanden links en rechts van de eerste groene waarnemer bevinden en met hem meebewegen. We zien dit in afbeelding 6. In deze afbeelding zijn ook twee gebeurtenissen met rode stippen aangegeven: de gebeurtenis “de lichtflits bereikt de linker groene waarnemer” en de gebeurtenis “de lichtflits bereikt de rechter groene waarnemer”. Nu komt de crux van het verhaal: vanuit de middelste groene waarnemer gezien staan de twee andere groene waarnemers stil, op gelijke afstanden van hem. Bovendien meet deze waarnemer een onveranderlijke lichtsnelheid – in het bijzonder moet het licht voor hem dus met dezelfde snelheid naar links als naar rechts bewegen. Het licht legt voor hem dus in beide richtingen dezelfde afstanden af met dezelfde snelheid – en moet dus links en rechts tegelijkertijd aankomen. Met andere woorden: voor de tweede waarnemer zijn de twee gebeurtenissen bij de rode stippen tegelijkertijd! Dit terwijl die gebeurtenissen voor onze oorspronkelijke, zwarte waarnemer, op heel verschillende tijdstippen plaatsvinden.

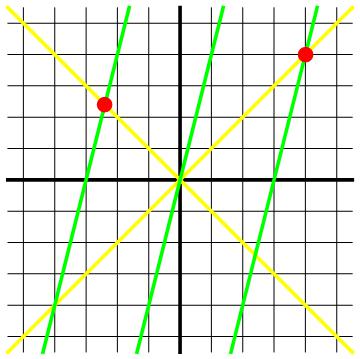
Afbeelding 6. Drie waarnemers.We voegen aan het vorige diagram nog twee extra groene waarnemers toe, die met dezelfde snelheid bewegen als de eerste. De rode stippen geven de gebeurtenissen aan waarop deze waarnemers het licht zien passeren. Voor de zwarte waarnemer gebeurt dit op heel verschillende tijdstippen (t=2,4s en t=4s), maar voor de middelste groene waarnemer zouden de gebeurtenissen tegelijkertijd moeten zijn!

Hoe kunnen de gebeurtenissen bij de twee rode stippen volgens de groene waarnemer tegelijkertijd zijn? Einstein beantwoordde deze vraag op de simpelst mogelijke manier, door de nieuwe groene lijn in afbeelding 7 te tekenen. Hij beweerde dat voor de tweede waarnemer de  gebeurtenissen op deze lijn de gebeurtenissen zijn die gelijktijdig plaatsvinden. Hetzelfde gedachtenexperiment kunnen we natuurlijk uithalen met groene waarnemers die dichter bij elkaar of verder van elkaar weg staan. Ook andere, parallelle groene lijnen geven dus verzamelingen gebeurtenissen weer die voor de groene waarnemers tegelijk plaatsvinden. In het bijzonder is de groene lijn die door de oorsprong gaat nu de x’-as: de verzameling van alle gebeurtenissen die volgens de groene waarnemers op t’=0 plaatsvinden. Het eindresultaat van deze redenering zien we in afbeelding 8.

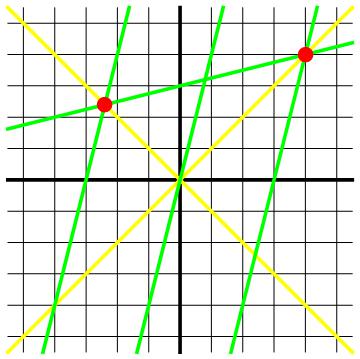
Afbeelding 7. Gelijktijdigheid in de relativiteitstheorie.Einsteins oplossing voor het probleem van de onveranderlijke lichtsnelheid: hij beweerde dat de nieuwe groene lijn gebeurtenissen weergeeft die voor de groene waarnemers op hetzelfde tijdstip plaatsvinden. Voor deze waarnemers zijn dus niet alleen de tijdlijnen, maar ook de ruimtelijnen gekanteld.

Als we afbeelding 8 vergelijken met afbeelding 5, zien we hoe belangrijk het was dat Einstein ruimte en tijd aan elkaar plakte tot de ruimtetijd. In tegenstelling met de klassieke natuurkunde zien verschillende waarnemers verschillende gebeurtenissen niet alleen op verschillende plaatsen, maar ook op verschillende tijdstippen. De ruimtetijd als geheel is hetzelfde “plaatje” voor beide waarnemers, maar hoe deze ruimtetijd wordt opgesplitst in “ruimte” en “tijd” hangt af van de snelheid van de waarnemer!

Afbeelding 8. Ruimte- en tijdlijnen voor de bewegende waarnemer.Het eindresultaat van Einsteins redenering. De dikke groene lijnen zijn de ruimte- en tijdassen van de groene waarnemers. De vlakke groene lijnen geven dus gebeurtenissen weer die voor die waarnemer dezelfde tijdcoördinaat hebben; de steile groene lijnen geven gebeurtenissen weer die voor die waarnemer dezelfde plaatscoördinaat hebben.

We zullen in de komende artikelen in dit dossier voorbeelden zien van de tegenintuïtieve gevolgen die dit “mengen” van ruimte en tijd met zich meebrengt. Een heel belangrijk voorbeeld van zo’n gevolg hebben we al gezien: gelijktijdigheid bestaat niet meer! De twee rode gebeurtenissen in afbeelding 7 zijn gelijktijdig voor de groene waarnemer, maar zijn dat beslist niet voor de zwarte.

Dat we dit verschijnsel (en andere verschijnselen die we in de volgende artikelen zullen tegenkomen) als enorm tegenintuïtief ervaren, komt doordat we in het dagelijks leven niets van dergelijke effecten merken. De reden daarvoor is dat we, om de effecten te zien, in ruimtetijddiagrammen als afbeelding 7 gebruik hebben moeten maken van nogal extreme eenheden en snelheden. Een gewoon vliegtuig, dat zich met 1000 km/u voortbeweegt, zou in afbeelding 7een traject volgen dat weergegeven wordt door een lijn die vrijwel verticaal is. De bijbehorende groene x’-as zou dan vrijwel horizontaal  zijn, en dus vrijwel samenvallen met de zwarte x-as. Gebeurtenissen die voor de stilstaande waarnemer gelijktijdig zijn, zijn voor de bewegende waarnemer – zelfs als die in een heel snel vliegtuig zit – dus nog vrijwel gelijktijdig. Pas als we zouden bewegen met een snelheid die in de buurt van de lichtsnelheid komt, merken we echt de effecten van het mengen van ruimte en tijd.

Onze intuïtie is gevormd bij lage snelheden, en we zijn dus totaal niet gewend aan dit soort effecten. We zullen bij het verder begrijpen van de relativiteitstheorie dus vooral moeten vertrouwen op ons vermogen om logisch te redeneren, en niet zozeer op onze intuïtie. We zullen zien dat dit vermogen ons ver brengt! Omgekeerd: loop niet in de val om “tegenintuïtief” met “fout” te verwarren. De relativiteitstheorie roept bij veel mensen die er voor het eerst mee kennismaken een grote weerstand op. De theorie kan echter volledig met logische argumenten onderbouwd worden – en belangrijker: de theorie kan vervolgens ook experimenteel getest worden! Intuïtie is voor een natuurkundige vaak een mooi hulpmiddel, maar kan als het gaat om de relativiteitstheorie ook een groot obstakel vormen.

Dit is het vierde artikel uit het dossier Relativiteitstheorie. In het vijfde artikel zullen we zien hoe verschillende waarnemers hun ruimtetijd-coördinaten in elkaar om kunnen rekenen.

Afbeelding blokkenschema: Lothar Spurzem.