Relativiteit (5): Lorentztransformaties

We hebben in het voorafgaande gezien dat we in de relativiteitstheorie ruimte en tijd moeten samenvoegen tot één geheel, de ruimtetijd. Verder hebben we ontdekt dat die ruimtetijd voor verschillende waarnemers, die zich ten opzichte van elkaar eenparig (met constante snelheid) bewegen, op verschillende manieren uiteenvalt in tijd en ruimte.

Voor het gemak hebben we in afbeelding 1 nog eens de situatie getekend. De verticale zwarte lijnen zijn de “tijdlijnen” van een eerste waarnemer: de gebeurtenissen die vanuit zijn oogpunt op dezelfde plaats maar op verschillende tijdstippen plaatsvinden. In het bijzonder is de dik gedrukte verticale zwarte lijn de positie waarop de waarnemer zich zelf op verschillende tijdstippen bevindt.  De horizontale zwarte lijnen zijn de “ruimtelijnen” van dezelfde waarnemer: de gebeurtenissen die van hem uit gezien op dezelfde tijdstippen maar op verschillende plaatsen plaatsvinden.

Afbeelding 1. De ruimtetijd.De ruimtetijd, met daarin de ruimte- en tijdlijnen van de zwarte en groene waarnemers.

De groene lijnen geven de opdeling van de ruimtetijd in ruimte en tijd voor de groene waarnemer weer. De dikgedrukte “staande” groene lijn is zijn eigen positie op verschillende tijdstippen: het is dus een van de lijnen die hij als “tijdlijn” ervaart. De andere staande groene lijnen zijn andere tijdlijnen: ook die lijnen geven gebeurtenissen weer die voor de groene waarnemer op dezelfde plaats (op dezelfde afstand) maar op verschillende tijdstippen plaatsvinden. De “liggende” groene lijnen zijn de ruimtelijnen van de groene waarnemer: de gebeurtenissen die van hem uit gezien op hetzelfde tijdstip maar op verschillende plaatsen plaatsvinden.

In dit artikel willen we twee belangrijke vragen beantwoorden die rijzen bij het bekijken van het diagram in afbeelding 1. Een eerste vraag is de volgende. Diagram 1 lijkt erg asymmetrisch: de ruimte- en tijdlijnen van de zwarte waarnemer staan netjes loodrecht op elkaar, terwijl de ruimte- en tijdlijnen van de groene waarnemer een hoek van minder dan 90 graden ten opzichte van elkaar maken. Het lijkt er in eerste instantie dus op dat de zwarte waarnemer de ruimtetijd “normaal” ervaart, terwijl de groene waarnemer een “platgedrukte” versie van de ruimtetijd waarneemt. Dit is in tegenspraak met het relativiteitsbeginsel: er lijkt nu weer een voorkeurswaarnemer te zijn (de zwarte) die we als stilstaand kunnen beschouwen.

Het is echter belangrijk dat we ons beseffen dat het loodrecht op elkaar staan van de ruimte- en tijdlijnen niets betekent. Dit is eenvoudigweg de manier waarop we gewend zijn grafieken te tekenen: één grootheid langs een horizontale as; een andere grootheid langs een loodrecht daarop staande verticale as. Als we zouden willen zouden we grafieken ook prima met schuine assen kunnen tekenen: in afbeelding 2 tekenen we bijvoorbeeld tweemaal dezelfde grafiek van een auto die over een weg rijdt; eenmaal met loodrechte assen, een eenmaal met schuine assen.

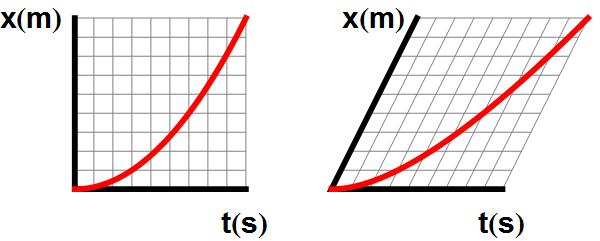
Afbeelding 2. Verschillende weergaven van dezelfde grafiek.Tweemaal dezelfde grafiek die de door een auto afgelegde afstand in de tijd weergeeft. In de eerste grafiek staan de assen loodrecht op elkaar, zoals gebruikelijk; in de tweede niet. Merk op dat beide grafieken bijvoorbeeld door de punten met coördinaten (0,0), (3,1), (6,4) en (9,9) gaan.

Andersom geredeneerd: we hadden het verhaal kunnen beginnen vanuit het oogpunt van de groene waarnemer, en het was dan logisch geweest om zijn ruimte- en tijdlijnen loodrecht op elkaar te tekenen. De zwarte waarnemer beweegt dan in het stelsel van de groene waarnemer met een bepaalde snelheid naar links, en we kunnen vervolgens in het diagram tekenen welke ruimte- en tijdlijnen hij ervaart. Dit leidt tot het diagram in afbeelding 3. We benadrukken nog eens dat het hier om precies dezelfde ruimtetijd gaat als in afbeelding 1, alleen op een andere manier weergegeven. Daarmee is de symmetrie (en dus het relativiteitsbeginsel) hersteld: voor het tekenen van een ruimtetijddiagram is het handig een bepaalde waarnemer als “stilstaand” te kiezen, maar de ruimtetijd zelf wordt door elke waarnemer precies hetzelfde ervaren.

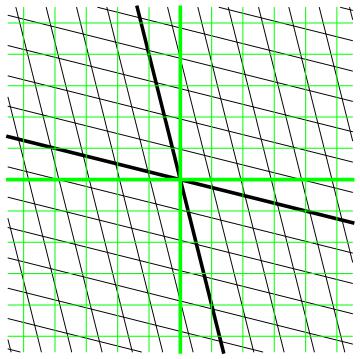
Afbeelding 3. De ruimtetijd voor de groene waarnemer.Dezelfde ruimtetijd als in afbeelding 1, maar getekend vanuit het perspectief van de groene waarnemer.

Een tweede vraag die rijst bij het bekijken van afbeelding 1 is: wat zijn de eenheden langs de assen? Ook hier hebben we weer een keuze gemaakt voor een “eerste” waarnemer. We hebben de zwarte ruimtelijnen zo getekend dat ze steeds 1 seconde van elkaar af liggen, dus zo dat de gebeurtenissen op twee boven elkaar liggende lijnen zich voor de zwarte waarnemer met 1 seconde tijdsverschil afspelen. De tijdlijnen hebben we zo getekend dat ze steeds 1 lichtseconde (zo’n 300.000 km) van elkaar af liggen: gebeurtenissen op twee naast elkaar liggende lijnen spelen zich voor de zwarte waarnemer af op plaatsen die 300.000 kilometer van elkaar verwijderd zijn.

De vraag is nu: hoe werkt dit voor de groene waarnemer? De dikgedrukte groene staande lijn in afbeelding 4 is de lijn waarlangs de waarnemer zelf beweegt – het zijn dus de punten waaraan hij plaatscoördinaat “x’ = 0 ls” toekent. ” (“ls” staat voor “lichtseconde”.) Maar wat is de lijn van punten waaraan hij plaats “x’ = 1 ls toekent? We hebben in afbeelding 4 twee gestippelde groene lijnen getekend waarvan het misschien voor de hand ligt dat het de lijnen zijn die we zoeken. De rechter lijn is de groene tijdlijn met de eigenschap dat die op t=0 s door een gebeurtenis gaat die voor de zwarte waarnemer een afstand van 1 lichtseconde heeft. De linker lijn is de groene tijdlijn met de eigenschap dat die op t’=0s door een gebeurtenis gaat die voor de zwarte waarnemer een afstand van 1 lichtseconde heeft. Merk echter op dat voor de constructie van allebei deze lijnen de zwarte waarnemer een cruciale rol speelt, terwijl we een vraag stellen die puur over de groene waarnemer gaat. Het lijkt dus wat onlogisch dat één van deze lijnen het juiste antwoord geeft, en dat blijkt ook niet het geval te zijn. De juiste groene tijdlijn op x’=1 ls blijkt ergens tussen deze twee tijdlijnen in te liggen: het is de niet gestippelde middelste groene tijdlijn in afbeelding 4. Voor de liefhebbers geven we de formule waarmee uit te rekenen valt waar deze lijn de zwarte x-as snijdt: dat is in het punt met

x = √(1-v²/c²) ls

Hierin is v de onderlinge snelheid van de waarnemers, en c de lichtsnelheid. Hoe Einstein uitvogelde dat juist dit de goede tijdlijn is zullen we later zien.

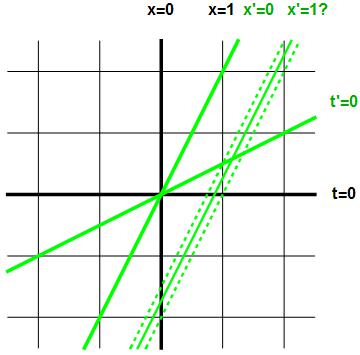
Afbeelding 4. Eenheden in de x’-richting.Welke lijn is de juiste tijdlijn op x’=1 lichtseconde?

Precies eenzelfde vraag kunnen we stellen voor de eenheden in de tijdrichting: wat is de groene ruimtelijn die de gebeurtenissen beschrijft die voor de groene waarnemer op t’ = 1s plaatsvinden? Afbeelding 5 is het equivalent van afbeelding 4 voor deze vraag; ook hier is weer niet direct uit onze figuren af te lezen wat de juiste lijn is. De juiste lijn is weer aangegeven; in de volgende artikelen zullen we zien met welk soort slimme redeneringen Einstein het antwoord wist te vinden. Voor de liefhebbers weer de formule, die erg lijkt op de bovenstaande: de groene ruimtelijn in afbeelding 5 snijdt de zwarte t-as in

t = √(1-v²/c²) s

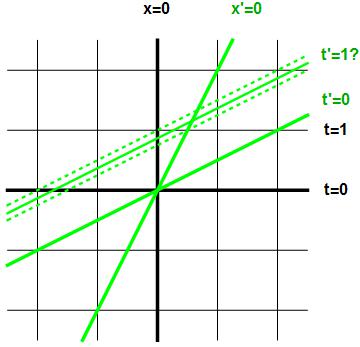
Afbeelding 5. Eenheden in de t’-richting.Welke lijn is de juiste ruimtelijn op t’=1 seconde?

Met deze informatie weten we dus niet alleen de richting waarin de groene ruimte- en tijdlijnen lopen, maar weten we ook de afstand die ze tot elkaar moeten hebben. (In de afbeeldingen 1 en 2 hebben we enigszins vals gespeeld, en de groene ruimte- en tijdlijnen direct al op de juiste afstanden getekend.) Daarmee hebben we voldoende informatie om de coördinaten van een gebeurtenis in het referentiekader van één waarnemer om te rekenen in coördinaten van een gebeurtenis in het referentiekader van een andere waarnemer. Zie bijvoorbeeld afbeelding 6: we zien dat de gebeurtenis met coördinaten x=5 ls , t=3 s in het zwarte stelsel, in het groene stelsel gegeven wordt door coördinaten die ongeveer gelijk zijn aan x’=4,5 ls, t’= 1,8 s.

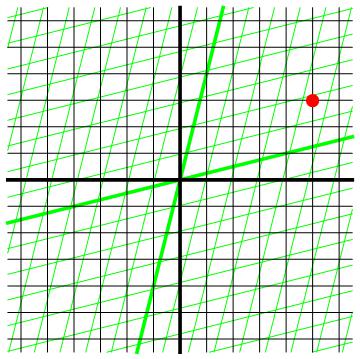
Afbeelding 6. Coördinaten vergelijken.De gebeurtenis die is weergegeven door de rode stip heeft in het zwarte referentiekader coördinaten (5,3), en in het groene referentiekader coördinaten (4,5, 1,8).

Voor de liefhebbers geven we hieronder weer de precieze formules waarmee de coördinaten in elkaar omgerekend kunnen worden:

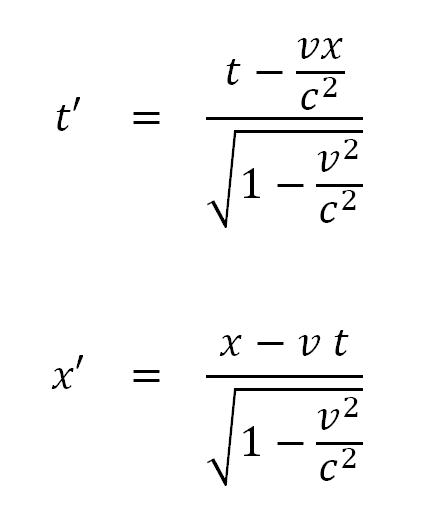
Afbeelding 7. De Lorentztransformaties.

Hierin staat v weer voor de onderlinge snelheid van de waarnemers, en c voor de lichtsnelheid.

De bovenstaande formules zien er al flink ingewikkeld uit. We zullen ze in wat volgt niet gebruiken, dus wie niet van wiskunde houdt, hoeft niet door de formules afgeschrikt te worden. Waar het om gaat is dat deze formules de relativistische variant zijn op de veel eenvoudigere Galileïtransformaties die we eerder zagen:

t’ = t
x’ = x – vt

Deze transformaties stelden ons in het klassieke geval in staat om coördinaten van de ene waarnemer in die van de andere om te rekenen. De nieuwe transformaties in afbeelding 7 doen precies hetzelfde in de relativistische ruimtetijd. De transformaties waren al bekend voordat Einstein zijn relativiteitstheorie opstelde: ze werden in 1892 beschreven door Hendrik Antoon Lorentz (die net als Einstein de Maxwellvergelijkingen bestudeerde), en heten daarom de Lorentztransformaties.

Een plaatje zegt meer dan duizend woorden, en zeker meer dan ingewikkelde wiskundige formules, dus laten we eens in een animatie kijken hoe de Lorentztransformaties precies werken. In afbeelding 8 zien we het zwarte coördinatenstelsel van de eerste waarnemer, en het groene coördinatenstelsel van de tweede waarnemer. In de animatie veranderen we langzaam de snelheid van de tweede waarnemer, van stilstand (ten opzichte van de zwarte waarnemer) tot de lichtsnelheid, en weer terug tot stilstand.

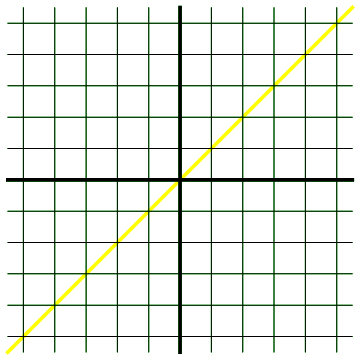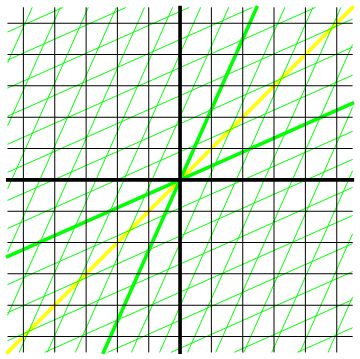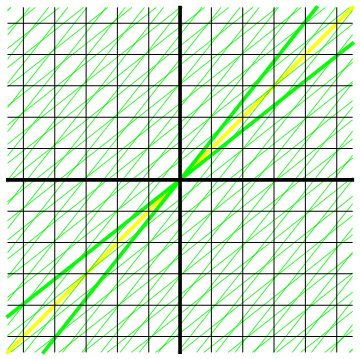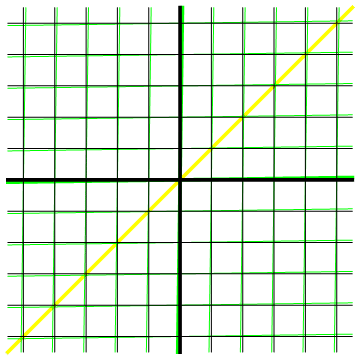
Afbeelding 8. Een animatie van de LorentztransformatiesHet referentiekader van de zwarte waarnemer wordt steeds vast gehouden; de groene ruimte- en tijdlijnen veranderen als de snelheid van de groene waarnemer verandert. De wereldlijn van de lichtflits is in alle referentiekaders diagonaal.

De precieze gevolgen van de Lorentztransformaties zullen we in de komende artikelen in dit dossier bestuderen, maar een aantal zaken is aan de animatie al meteen duidelijk. Ten eerste zien we heel goed dat het begrip gelijktijdigheid geen waarnemeronafhankelijke betekenis meer heeft: alle waarnemers hebben ruimtelijnen die van hun snelheid afhankelijk zijn, en iedere waarnemer heeft dus zijn eigen notie van gelijktijdigheid. Ten tweede zien we dat ook afstanden en tijdsintervallen waarnemerafhankelijk zijn: de afstand tussen de ruimte- en tijdlijnen van de groene waarnemer verandert continu als we zijn snelheid veranderen. We zullen de gevolgen voor afstanden en tijdsintervallen in de relativiteitstheorie in de volgende twee artikelen in dit dossier uitgebreid bespreken.

In deze zee van veranderlijkheid zien we ook een constante factor. De diagonale gele lijn in afbeelding 8 is ook voor alle groene waarnemers diagonaal. In het zwarte referentiekader beschrijft deze lijn de voortplanting  van een lichtflits door de ruimtetijd: steeds als het 1 seconde later is (1 vakje naar boven) is de lichtflits ook 1 lichtseconde opgeschoven (1 vakje naar rechts). Precies hetzelfde geldt voor alle andere waarnemers. Met andere woorden: het licht beweegt in alle referentiekaders met precies dezelfde snelheid! Dit resultaat was het oorspronkelijke doel van onze exercitie; het is goed om te zien dat we dit doel inderdaad bereikt hebben.

Dit is het vijfde artikel uit het dossier Relativiteitstheorie. In het zesde artikel komen we een belangrijke voorspelling van Einsteins theorie tegen: de tijdsdilatatie – het verschijnsel dat bewegende klokken langzamer lopen.