Relativiteit (9): Een snelheidslimiet

We zijn onze discussie over de relativiteitstheorie begonnen met het verrassende maar experimenteel testbare feit dat het licht een onveranderlijke en voor iedere waarnemer even grote snelheid heeft. We zagen toen direct al dat dit tot gevolg heeft dat snelheden in de ruimtetijd niet eenvoudigweg opgeteld kunnen worden, zoals we in het dagelijks leven wel gewend zijn te doen. Als er een lichtstraal van links naar rechts beweegt met 300.000 km/s, en een waarnemer beweegt van rechts naar links met 100.000 km/s, dan ziet de waarnemer het licht niet met 300.000 + 100.000 = 400.000 km/s op zich af komen, maar nog altijd met 300.000 km/s.

Aan de andere kant verwachten we dat bij lage snelheden onze intuïtie over het optellen van snelheden vrijwel juist is. Als een auto met 30 km/u naar rechts rijdt, en botst met een hardloper die met 10 km/u naar links rent, weten we dat de hardloper de botsing zal ervaren alsof de auto met 30 + 10 = 40 km/u op hem af komt. Aan de andere kant weten we dit ervaringsfeit natuurlijk niet met 100% precisie. Het zou dus kunnen dat de hardloper in feite een relatieve snelheid van 39,999… km/u ervaart, waardoor onze dagelijkse ervaring (net zoals experimenten die niet met extreme nauwkeurigheid gedaan worden) het verschil met de exacte 40 km/u niet waarneemt.

Kortom: we verwachten dat er een manier is om het “relativistisch optellen” van snelheden te beschrijven, zodanig dat die manier bij alledaagse snelheden vrijwel gelijk is aan het gewone optellen, maar bij hoge snelheden ertoe zorgt dat de lichtsnelheid, bij welke snelheid we die ook “optellen”, altijd weer gelijk is aan de lichtsnelheid.

Met behulp van een ruimtetijddiagram kunnen we zien dat een dergelijke manier van relativistisch optellen inderdaad bestaat. We nemen hiervoor het volgende voorbeeld. Een trein rijdt ten opzichte van het station, dat we voor het gemak als “stilstaand” beschouwen, met een derde van de lichtsnelheid naar rechts. In deze trein beweegt een supersonische hardloper, die ten opzichte van de trein zelf ook met een derde van de lichtsnelheid naar rechts beweegt. Hoe hard beweegt de hardloper dan ten opzichte van het station?

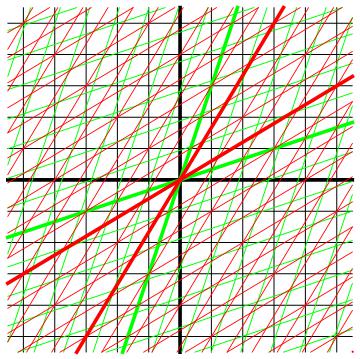
Afbeelding 1. Snelheden optellen.De referentiekaders van het station (zwart), van de trein (groen) en van de hardloper (rood).

In afbeelding 1 zien we een ruimtetijddiagram dat deze situatie weergeeft. We hebben in dit diagram drie referentiekaders getekend: de ruimtetijdassen van het station in het zwart, de ruimtetijdassen van de rijdende trein in het groen, en de ruimtetijdassen van de supersonische hardloper in het rood. Omdat deze figuur door alle lijnen nogal chaotisch word hebben we in afbeelding 2 drie deelfiguren getekend, waarin steeds één van de drie stelsels is weggelaten.

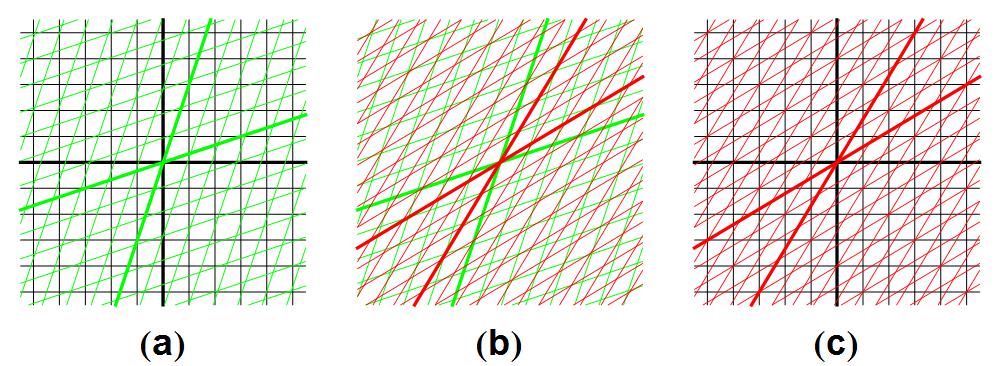
Afbeelding 2. Snelheden optellen.(a) De referentiekaders van het station en de trein. (b) De referentiekaders van de trein en de hardloper. (c) De referentiekaders van het station en de hardloper. In het laatste diagram kunnen we aflezen dat de hardloper met 60% van de lichtsnelheid beweegt ten opzichte van het station.

Laten we nu eerst eens kijken naar afbeelding 2a. We hebben hier allereerst de ruimtetijdlijnen van het station getekend, gewoon door hokjes van 1 seconde bij 1 lichtseconde te tekenen, zoals we altijd doen. Vervolgens hebben we met behulp van de inmiddels bekende Lorentztransformaties de groene ruimtetijdlijnen in dit stelsel weergegeven. We kunnen inderdaad zien dat de trein met een derde van de lichtsnelheid reist: de wereldlijn van de trein heeft een helling die zo gekozen is dat de trein één lichtseconde aflegt (één hokje naar rechts) in drie seconden (drie hokjes naar boven). We zien inderdaad dat de wereldlijn van de trein door het punt (1,3) in de afbeelding gaat.

In afbeelding 2b hebben we precies hetzelfde gedaan, maar nu hebben we eerst alleen het al bekende referentiekader van de trein getekend, en hierin met rood een nieuw referentiekader getekend dat zo gekozen is dat de wereldlijn van de hardloper in de nieuwe coördinaten door het punt (1,3) gaat. Met andere woorden: de hardloper legt ten opzichte van de trein in t’=3 s weer x’ = 1 ls af – hij loopt ten opzichte van de trein met een derde van de snelheid van het licht.

Nu leggen we in afbeelding 2c het zwarte en het rode referentiekader over elkaar heen. In deze afbeelding kunnen we vervolgens aflezen hoe snel de hardloper beweegt ten opzichte van het station. We zien dat de wereldlijn van de hardloper bijvoorbeeld door het punt (3,5) gaat: in 5 seconden legt de hardloper ten opzichte van het station 3 lichtseconden af. De hardloper beweegt ten opzichte van het station dus met 3/5 (oftewel: 60%) van de lichtsnelheid. Beduidend langzamer dan we zouden verwachten als we de twee snelheden “klassiek” hadden opgeteld: dan zouden we verwacht hebben dat de hardloper ten opzichte van het station met 1/3 + 1/3 = 2/3, dus zo’n 67% van de lichtsnelheid zou hebben bewogen!

We zien dat we op deze manier “grafisch” snelheden kunnen optellen. Wie handig is met meetkunde kan aan de hand van deze grafische methode ook een formule voor het optellen van twee snelheiden afleiden; voor de liefhebbers geven we deze formule hier. Als we een snelheid u bij een snelheid v “relativistisch optellen”, vinden we het resultaat

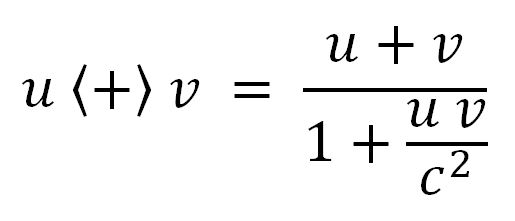
We gebruiken hier de notatie <+> voor relativistisch optellen, een handige notatie die we hebben overgenomen uit het zeer leesbare boek “De sublieme eenvoud van de relativiteit” van Sander Bais.

We kunnen nu controleren dat deze nieuwe manier van optellen aan de twee voorwaarden voldoet die we aan het begin van dit artikel noemden.

1. Bij zeer lage snelheden liggen de tijdassen van alle referentiekaders vrijwel verticaal. Het maakt dus nauwelijks uit of we in het stilstaande of het bewegende referentiekader één vakje omhoog bewegen. Als we dus eerst “v” vakjes opzij bewegen en één vakje omhoog in het eerste stelsel (wat overeenkomt met een snelheid van v vakjes per seconde) en vervolgens “u” vakjes opzij en één vakje omhoog in het tweede stelsel (wat overeenkomt met een snelheid van “u” vakjes per seconde in het tweede stelsel) is dit vrijwel hetzelfde als “u+v” vakjes opzij bewegen in het oorspronkelijke stelsel. We zullen dus een snelheid vinden uit de relativistische optelling die vlakbij het intuïtieve antwoord van u+v ligt. Ook aan de formule hierboven is dit te zien: de noemer van de breuk zal, voor snelheden die veel kleiner zijn dan de lichtsnelheid c, vlak bij 1 liggen, zodat het antwoord vrijwel gelijk is aan u+v. Met de getallen uit ons allereerste voorbeeld vinden we uit de formule bijvoorbeeld dat 30 km/u <+> 10 km/u gelijk is aan 39,9999999999999897 km/u. (Let op: wie deze berekening zelf met de formule wil doen moet eraan denken dat we dezelfde eenheden voor alle snelheden moeten gebruiken. We moeten dus eerst ofwel de lichtsnelheid omrekenen in km/u, ofwel de snelheden van de auto en de hardloper in km/s.) Het is geen wonder dat we het minieme verschil met het intuïtieve antwoord van 40 km/u in het dagelijks leven niet merken!
2. Als we bij een willekeurige snelheid de lichtsnelheid optellen moeten we in het nieuwe (groene) referentiekader een (rode) lijn tekenen die één vakje opzij en één vakje omhoog gaat. Aan afbeeldingen zoals afbeelding 2a zien we dat deze lijn in beide stelsels een diagonale lijn is – de lijn gaat dus ook in het oorspronkelijke stelsel één vakje opzij en één vakje omhoog. Met andere woorden: het resultaat is ook in het oorspronkelijke stelsel de lichtsnelheid! In een formule: u <+> c = c voor elke waarde van u. Wie handig is met algebra kan dit ook afleiden uit de formule hierboven.

We hebben nu gezien hoe we relativistisch snelheden kunnen optellen. Een bijzondere eigenschap van deze optelling is dat als we twee snelheden kleiner dan de lichtsnelheid optellen, het resultaat ook altijd kleiner dan de lichtsnelheid zal zijn. Als we immers de lichtsnelheid zelf bij een andere snelheid optellen, vinden we weer de lichtsnelheid – optellen van een iets kleinere snelheid moet dus ook een iets kleiner resultaat geven. Met behulp van de formule vinden we bijvoorbeeld dat het optellen van twee snelheden die elk 99% van de lichtsnelheid zijn, een resultaat geeft dat 99,9949% van de lichtsnelheid is – vrijwel de lichtsnelheid, maar nog net iets kleiner. Met andere woorden: we kunnen snelheden optellen zoveel als we willen, maar we zullen nooit op of boven de lichtsnelheid uitkomen!

Dit rekenkundige resultaat werd door Einstein in een fysisch principe omgezet. Als we een voorwerp versnellen doen we immers niets anders dan steeds een klein beetje snelheid “toevoegen”, oftewel: steeds een klein beetje snelheid bij de al aanwezige snelheid optellen. Maar voor deze optelling moeten we in de relativiteitstheorie de relativistische optelling gebruiken – het resultaat zal dus altijd kleiner blijven dan de lichtsnelheid!

Hoe veel we een voorwerp dat nog niet met de lichtsnelheid beweegt ook versnellen, het zal nooit sneller gaan bewegen dan het licht.

In het heelal is de lichtsnelheid dus een soort “maximumsnelheid”! Let op: er zijn wel “voorwerpen” in het heelal die al met de lichtsnelheid bewegen: fotonen (lichtdeeltjes) zijn hier een voorbeeld van. Voor deze deeltjes geldt het omgekeerde: welke snelheid we ook van hun snelheid aftrekken, we krijgen altijd weer de lichtsnelheid als resultaat. Fotonen kunnen dus niet afgeremd worden, en bewegen altijd met de lichtsnelheid! De reden dat fotonen (en andere deeltjes) deze eigenschap hebben, is dat ze geen massa hebben. Het kost daardoor in zekere zin geen energie om ze te versnellen, en ze worden automatisch “maximaal versneld”.

Uit het maximaal zijn van de lichtsnelheid wist Einstein één van zijn beroemdste formules af te leiden: de formule E=mc². Deze formule zegt dat massa (weergegeven door de letter m) een vorm van energie is (weergegeven door de letter E), en dat de twee in elkaar omgerekend kunnen worden door de massa tweemaal met de lichtsnelheid (dus met c²) te vermenigvuldigen. Het getal c² is in onze alledaagse eenheden natuurlijk een gigantisch groot getal – een klein beetje massa komt dus overeen met een enorme hoeveelheid energie. Dit principe wordt in kernreactoren nuttig gebruikt om energie uit radioactieve atomen te winnen, en is op veel destructievere wijze gebruikt bij het ontploffen van de eerste atoombommen.

Afbeelding 3. Een kernreactor.In een kernreactor wordt uit massa energie gewonnen volgens Einsteins beroemde formule E=mc². Hier de kerncentrale bij Civaux in Frankrijk. (Foto: Greudin.)

Het zou te ver voeren om Einsteins afleiding van de formule E=mc² hier precies te herhalen – wie daarin geïnteresseerd is kan een pittige maar begrijpelijk geformuleerde wiskundige afleiding bijvoorbeeld vinden in het al eerder genoemde boekje “De sublieme eenvoud van de relativiteit”  van Sander Bais. Hier willen we de omgekeerde weg bewandelen, en beredeneren dat de formule E=mc² impliceert dat er inderdaad een grens aan het versnellen van voorwerpen moet zijn.

We beginnen hiervoor met de volgende eenvoudige opmerking:

Zwaardere voorwerpen zijn moeilijker te versnellen.

Dit ervaringsfeit kennen we uit het dagelijks leven. Als we een trap tegen een speelgoedautootje geven zal het autootje met een flinke snelheid beginnen te rijden. Als we een trap tegen een veel zwaardere vrachtauto geven zal deze nauwelijks versnellen. Hoe zwaarder iets dus is, hoe lastiger het te versnellen is.

Met behulp van Einsteins formule zien we nu dat ook een tweede bewering geldig is:

Voorwerpen die sneller bewegen zijn zwaarder.

Een bewegend voorwerp heeft namelijk meer energie dan hetzelfde voorwerp in stilstand; de zogenaamde bewegingsenergie of kinetische energie. Als we Einsteins formule de andere kant op lezen, beseffen we dat deze energie overeenkomt met een bepaalde (voor alledaagse snelheden heel kleine) hoeveelheid massa, en dat een bewegend voorwerp dus iets zwaarder is dan een voorwerp in stilstand. Alweer een bevreemdend effect van de relativiteitstheorie, en alweer een effect dat in ons dagelijks leven volkomen verwaarloosbaar is, maar ook alweer een effect dat we in experimenten kunnen waarnemen.

Nu plakken we de bovenstaande twee ideeën aan elkaar. We beginnen met een betrekkelijk licht voorwerp, en geven hier een flinke trap tegen. Het voorwerp zal versnellen, en daardoor íets zwaarder worden. Vervolgens geven we een tweede, even grote trap tegen het voorwerp. Het voorwerp zal wederom versnellen, maar doordat het voorwerp nu iets zwaarder is, zal deze versnelling iets kleiner zijn dan de eerste. Met zijn nog hogere snelheid is het voorwerp nu nog iets zwaarder, dus de derde trap die we geven zal nog iets minder effect hebben, enzovoort. Elke achtereenvolgende trap heeft een kleiner effect, en we kunnen ons dus afvragen of we op deze manier, hoe vaak we ook trappen, niet een bepaalde grens in snelheid bereiken die we steeds dichter naderen maar nooit zullen overschrijden.

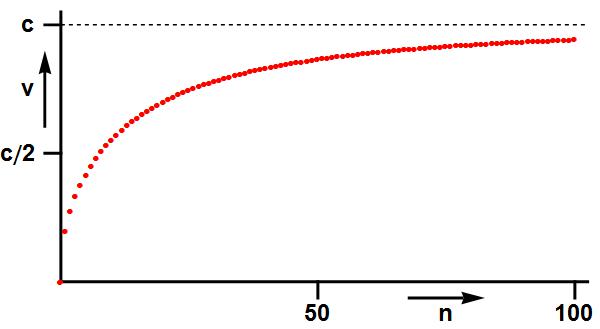
Afbeelding 4. Een grens aan versnelling.Een computermodel van het hier beschreven experiment. We geven een voorwerp 100 maal een duw, waarbij zijn energie steeds toeneemt met 2% van zijn rustenergie. (Dat wil zeggen: met een vaste hoeveelheid energie die gelijk is aan 2% van m­­₀c², met m₀ de massa gemeten in rust.) We zien dat de snelheid v steeds toeneemt, maar dat die toename ook steeds kleiner wordt. De snelheid nadert de lichtsnelheid steeds meer, maar overschrijdt deze nooit.

Het antwoord zal inmiddels niet meer verbazen: zo’n snelheidsgrens is er inderdaad, en Einstein rekende uit dat deze snelheidsgrens precies de lichtsnelheid is. Ook uit de formule E=mc² kunnen we op die manier dus afleiden dat de lichtsnelheid een maximale snelheid is. (Zoals eerder gezegd: in Einsteins geval ging deze afleiding in zekere zin andersom; hij kwam uit bij de formule E=mc².)

We zijn nu uitgekomen bij misschien wel de belangrijkste formule uit de hele relativiteitstheorie, en hebben daarmee ons verhaal over de speciale relativiteitstheorie afgerond. Maar Einstein ging verder: in de jaren na het afronden van de speciale relativiteitstheorie werkte hij aan een uitbreiding van die theorie die de algemene relativiteitstheorie genoemd zou worden. Wat is er dan zo speciaal aan de speciale relativiteitstheorie, en waarom is er een veralgemenisering nodig? Dat zullen we zien in het volgende artikel in dit dossier.

Dit is het negende artikel uit het dossier Relativiteitstheorie. In het tiende artikel bespreken we het equivalentieprincipe, dat de basis vormt voor de algemene relativiteitstheorie.