Relativiteit (3): Galileitransformaties

Afbeelding 1. Galileo Galilei.Schilderij van Justus Sustermans.

Laten we eens beter kijken naar de manier waarop we in de klassieke natuurkunde ruimte en tijd beschrijven. Natuurkunde gaat over gebeurtenissen, en een gebeurtenis vindt over het algemeen plaats op een bepaald moment en op een bepaalde plaats. Om dat moment en die plaats aan te geven, maken we gebruik van coördinaten. Aangezien ons heelal driedimensionaal is, hebben we voor het beschrijven van een plaats drie coördinaten nodig. (Zie ook het artikel over dimensies.) We kunnen bijvoorbeeld zeggen dat een gebeurtenis plaatsvindt op een plek die drie meter rechts van een bepaald referentiepunt ligt, twee meter verder naar voren, en zes meter hoger. In coördinaten beschreven, vindt de gebeurtenis dan dus plaats op het punt (3,2,6). Merk op dat voor het gebruik van coördinaten naast de keuze van drie richtingen ook de keuze van een referentiepunt (of oorsprong) nodig is.

Ook het tijdstip van een gebeurtenis kunnen we aangeven met een coördinaat, en ook hiervoor hebben we een bepaald referentiepunt nodig. Als referentiepunt kunnen we bijvoorbeeld het tijdstip kiezen waarop de zon haar hoogste punt aan de hemel bereikt, en we kunnen dan zeggen dat de gebeurtenis “het avondeten staat klaar” zes uur en vijftien minuten na dat referentietijdstip plaatsvindt.

In totaal hebben we voor het beschrijven van een natuurkundige gebeurtenis dus vier coördinaten nodig: drie ruimtecoördinaten en een tijdcoördinaat. Het feit dat we drie ruimtecoördinaten hebben, is voor het begrijpen van de relativiteitstheorie eigenlijk een overbodige luxe. De principes van de theorie laten zich prima uitleggen aan de hand van maar één ruimtecoördinaat. Vanaf nu gaan we er dus van uit dat we alleen maar geïnteresseerd zijn in posities die volledig links of rechts van ons referentiepunt liggen; niet in posities die zich daar ook boven, onder, voor of achter bevinden. Met andere woorden: we beschrijven een vereenvoudigde, eendimensionale ruimte met maar één coördinaat, die we de x-coördinaat zullen noemen. De tijdscoördinaat die gebeurtenissen aangeeft noemen we in het vervolg de t-coördinaat. Een gebeurtenis die zich drie meter rechts van ons referentiepunt afspeelt, op twee seconden na ons referentietijdstip, kunnen we dus aangeven met de coördinaten x=3m, t=2s.

Het staat iedereen natuurlijk vrij om zijn eigen coördinatenstelsel te kiezen. Iedereen kan dus zijn eigen referentiepunt (zowel in ruimte als in tijd) kiezen, en kan de afstanden en tijden ten opzichte van dat punt in zijn eigen eenheden meten: meters, mijlen of voeten voor afstanden, secondes, uren of jaren voor tijdstippen. We gaan er in het nu volgende van uit dat verschillende waarnemers afspraken hebben gemaakt over het gebruik van dezelfde eenheden, en over de keuze van één gebeurtenis (bijvoorbeeld een startschot) die ze gebruiken als hun referentiepunt in ruimte en tijd. Deze gebeurtenis wordt dus voor elke waarnemer beschreven met de coördinaten x=0m, t=0s.

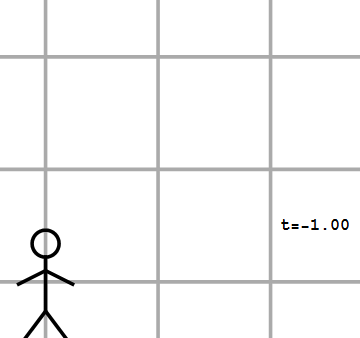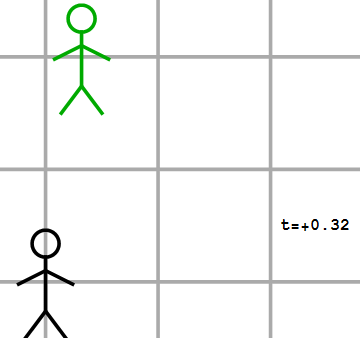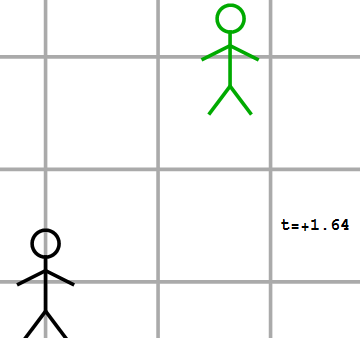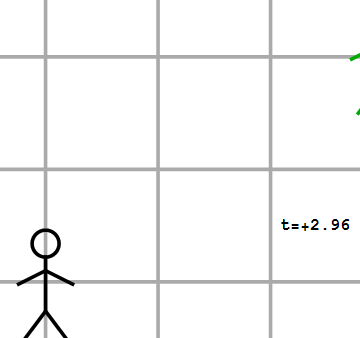
Afbeelding 2.De zwarte waarnemer ziet een gele lichtflits op t=0s, x=0m, en een rode lichtflits op t=2s, x=0m.

Betekent dit dat zulke waarnemers aan elke andere gebeurtenis ook dezelfde coördinaten toekennen? Dat hoeft beslist niet! Laten we bijvoorbeeld eens kijken naar twee waarnemers die niet stilstaan ten opzichte van elkaar, maar waarvan de een eenparig beweegt (dus: met een constante snelheid) ten opzichte van de ander. We geven deze waarnemers in de afbeeldingen 2 en 3 weer als een zwarte en een groene waarnemer. Naast de gebeurtenis van het startschot (aangegeven met een gele “flits” nemen deze twee waarnemers nog een tweede gebeurtenis waar – het ontploffen van een rotje, aangegeven met een rode flits. Voor de zwarte waarnemer vindt deze gebeurtenis plaats op dezelfde plaats als het startschot (dus op de plaats x=0m), 2 seconden na het startschot (dus op het tijdstip t=2s).

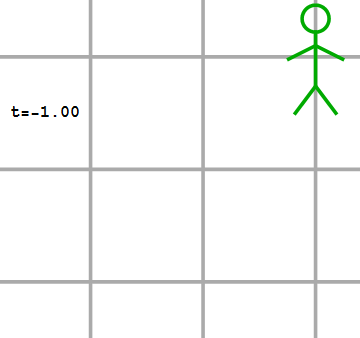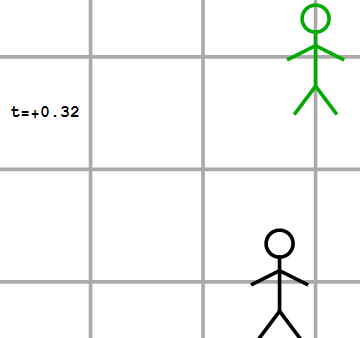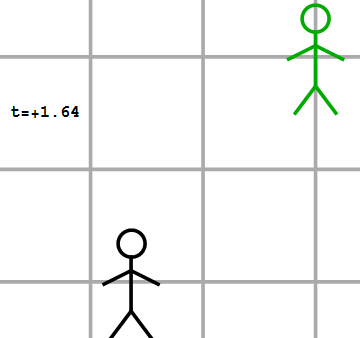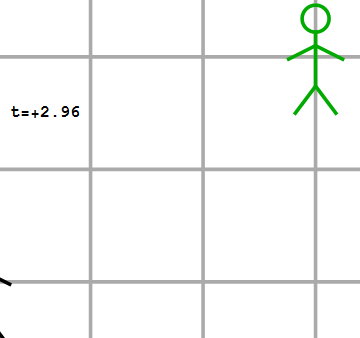
Afbeelding 3.De groene waarnemer ziet een gele lichtflits op t=0s, x’=0m, en een rode lichtflits op t=2s, x=-2m.

Welke coördinaten kent de groene waarnemer aan deze tweede gebeurtenis toe? In afbeelding 3 zien we de situatie zoals we die normaalgesproken in de klassieke natuurkunde beschrijven. Hierin is één belangrijke aanname al duidelijk te zien: de tweede waarnemer ziet het rotje ontploffen op precies hetzelfde tijdstip als de eerste waarnemer. Met andere woorden: tijd is absoluut; volgens verschillende waarnemers vindt dezelfde gebeurtenis op hetzelfde tijdstip plaats. Dat dit zo is, is geen natuurwet die we hebben afgeleid, maar simpelweg een ervaringsfeit. Als ik iemand vertel dat ik vanuit een bewegende trein om 13:47 uur een zonsverduistering heb waargenomen, zal die persoon, als die naast de trein stilstond en de zonsverduistering ook gezien heeft, mij ook vertellen dat die gebeurtenis om 13:47 plaatsvond. In de klassieke natuurkunde is het feit dat tijdstippen absoluut (dus: waarnemeronafhankelijk) zijn dus een aanname, die goed overeen lijkt te komen met de praktijk.

Over de tijdscoördinaat van de rode flits zullen beide waarnemers het in ons klassieke beeld dus eens zijn. Over de plaatscoördinaat van de rode flits zijn ze dat echter niet. In afbeelding 2 zien we dat de zwarte waarnemer de flits in zijn coördinatenstelsel op positie x=0m waarneemt. Voor de groene waarnemer is het, omdat hij zichzelf als stilstaand zal ervaren (alweer het relativiteitsbeginsel!) echter veel logischer om coördinaten te gebruiken waarin hij zelf altijd op coördinaat x’=0m blijft. (We voegen hier een accent aan de x toe om aan te geven dat het gaat om de coördinaat die de groene waarnemer gebruikt.) Als gevolg daarvan zal de groene waarnemer, die met 1 meter per seconde naar rechts beweegt ten opzichte van de zwarte, al twee meter verderop zijn als het rotje ontploft, en die ontploffing in zijn coördinaten dus op x’=-2m zien gebeuren.

We kunnen deze bevindingen samenvatten in twee eenvoudige formules. Allereerst hebben we gezien dat, in de klassieke natuurkunde, waarnemers het eens zijn over het tijdstip waarop een gebeurtenis plaatsvindt. De tijdcoördinaat t die de zwarte waarnemer aan zo’n gebeurtenis toekent, zal dus gelijk zijn aan de tijdcoördinaat t’ die de groene waarnemer eraan toekent:

t’=t

De plaatscoördinaat x’ die de groene waarnemer voor gebeurtenissen gebruikt, “verschuift” echter langzaam ten opzichte van de plaatscoördinaat x die de zwarte waarnemer gebruikt. In een formule ziet dat er als volgt uit:

x’=x-vt

In woorden: de onderlinge verschuiving tussen de twee coördinaten is gelijk aan de onderlinge snelheid van de twee waarnemers (v) maal de verstreken tijd (t). De bovenstaande twee eenvoudige formules worden de Galileïtransformaties genoemd. Ze geven aan hoe we de coördinaten van een gebeurtenis voor de ene waarnemer kunnen omrekenen in coördinaten voor de andere waarnemer. We willen twee belangrijke eigenschappen van deze transformaties benadrukken.

1. Zoals al eerder gezegd berusten ze op de aanname dat tijd absoluut is. Deze aanname komt goed overeen met onze dagelijkse ervaringen, maar we zullen later zien dat ze toch onjuist is!
2. Onze gebruikelijke intuïtie dat we snelheden kunnen optellen en aftrekken, is equivalent met de tweede Galileïtransformatie. Als de eerste, zwarte waarnemer de positie van een rijdende trein bijvoorbeeld met x aangeeft, zal de tweede, groene waarnemer die positie op twee manieren zien veranderen. Er is de verandering in x zelf, dus de snelheid van de trein ten opzichte van de zwarte waarnemer, en er is de verandering ten gevolge van de beweging van de groene waarnemer zelf, die in de formule met de term v t wordt aangegeven. Deze twee veranderingen worden in de formule simpelweg van elkaar afgetrokken – we doen dus niets anders dan de snelheden van elkaar aftrekken.

Zoals we gezien hebben is het dit tweede punt waarmee de Maxwellvergelijkingen in tegenspraak zijn: het optellen en aftrekken van snelheden is in tegenspraak met het feit dat de lichtsnelheid voor elke waarnemer hetzelfde is. Om deze “bug” te corrigeren, zullen we dus de tweede Galileïtransformatie moeten aanpassen. Dit was precies wat Einstein deed – en in dat proces ontdekte hij dat de eerste Galileïtransformatie ook niet helemaal klopt. Met andere woorden: hoewel we denken dat tijd absoluut en dus waarnemeronafhankelijk is, blijkt dat niet het geval te zijn! De reden dat we dit in het dagelijks leven niet merken, is dat in normale situaties de waargenomen tijdstippen t en t’ wel bijna hetzelfde zullen zijn. Zoals we zullen zien, worden tijdstippen die waarnemers meten pas significant verschillend als die waarnemers ten opzichte van elkaar met bijna de lichtsnelheid bewegen – iets wat in het dagelijks leven natuurlijk nooit voorkomt.

Afbeelding 4.Het begin van het beroemde artikel waarin Einstein zijn speciale relativiteitstheorie uiteenzette.

Nu we goed begrijpen hoe we in de klassieke natuurkunde met behulp van Galileïtransformaties, ruimte en tijd beschrijven, wordt het hoog tijd om eens te kijken naar de wijzigingen die Einstein in deze beschrijving aanbracht. Hij begon daarmee met een zeer eenvoudig idee: het aan elkaar plakken van de ruimte en de tijd in één geheel: de ruimtetijd.

Dit is het derde artikel uit het dossier Relativiteitstheorie. In het vierde artikel zien we hoe Einstein de ruimte en de tijd samenvoegde tot één geheel: de ruimtetijd.