Relativiteit (7): Lorentzcontractie

In afbeelding 1 zien we het inmiddels bekende plaatje: de ruimtetijd met daarin de ruimte- en tijdlijnen van de zwarte waarnemer en de ruimte- en tijdlijnen van de groene waarnemer. Laten we nu eens specifiek kijken naar de twee dik gedrukte groene lijnen die de rand van het lichtgroene vlak vormen. Dit zijn de lijnen die voor de groene waarnemer de coördinaten x’=0 ls en x’=1 ls weergeven. We kunnen ons hierbij bijvoorbeeld voorstellen dat de groene waarnemer een (enorme) meetlat van 300.000 kilometer lengte bij zich heeft, en dat de twee dik gedrukte groene lijnen de wereldlijnen van de twee uiteinden van de meetlat weergeven.

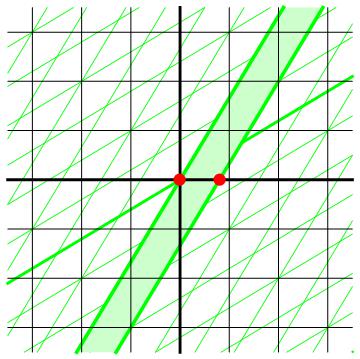
Afbeelding 1. Lorentzcontractie.De groene lijnen aan de zijkanten van het lichtgroene vlak zijn de lijnen waarvoor x’=0 ls en x’=1 ls. We kunnen deze lijnen zien als de wereldlijnen van de uiteinden van een meetlat van 1 ls lengte die de groene waarnemer bij zich heeft. Voor de zwarte waarnemer lijkt de meetlat maar 0,8 ls lang.

Op wat voor afstand van elkaar ziet de zwarte waarnemer deze twee uiteinden passeren? We kunnen dit gemakkelijk aflezen uit het diagram: bij deze specifieke snelheid (zo’n 60% van de lichtsnelheid) liggen de twee rode stippen in het diagram, die de posities van de uiteinden op t=0 s weergeven, zo’n 0,8 ls van elkaar af. De meetlat ziet er voor de zwarte waarnemer dus zo’n 20% korter uit! Bewegende voorwerpen lijken kennelijk korter dan diezelfde voorwerpen in stilstand zijn. Of, beter geformuleerd: ze lijken korter dan ze lijken voor een waarnemer die met de voorwerpen meebeweegt. Dit verschijnsel wordt Lorentzcontractie genoemd. Soms wordt ook de term Lorentz-FitzGeraldcontractie gebruikt, en in het nieuwe natuurkundecurriculum voor de middelbare school komt de term ruimtekrimp voor.

Ook de Lorentzcontractie is een ongebruikelijk verschijnsel uit de relativiteitstheorie dat we moeilijk met onze dagelijkse intuïtie kunnen rijmen. Ook hier is het dus van belang om met behulp van experimenten te testen of bewegende voorwerpen inderdaad korter worden. Op grote schaal is zo’n test lastig uit te voeren: we kunnen nu eenmaal geen grote voorwerpen versnellen tot dicht bij de lichtsnelheid. Op atomaire schaal is het meten van Lorentzcontractie echter veel eenvoudiger. Zo kunnen we geladen atomen (ionen) met grote snelheden op elkaar afvuren, en waarnemen hoe de brokstukken na de botsing wegvliegen. De ionen zijn in rust vrijwel bolvormig, maar door de Lorentzcontractie worden ze, vanuit het laboratorium gezien, samengedrukt in hun bewegingsrichting en hebben ze dus de vorm van platte pannenkoeken die op elkaar af vliegen. De manier waarop de brokstukken uiteenvliegen, blijkt inderdaad consistent te zijn met deze pannenkoekvorm, en niet met een bolvorm.

Ook het in het vorige artikel genoemde experiment met vervallende muonen kunnen we zien als een bevestiging van het verschijnsel van Lorentzcontractie. Gezien vanaf de aarde konden we dit verschijnsel verklaren door te zeggen dat de “interne klok” van de muonen langzamer loopt, waardoor er minder muonen vervallen dan we zouden verwachten, en er dus meer het aardoppervlak bereiken. Hoe zit dat echter voor een fictieve waarnemer die met de muonen meereist door de dampkring? Voor hem staan de muonen stil, en moet de vervaltijd dus de normale korte vervaltijd zijn. Hoe kan het dan dat er toch zoveel muonen het aardoppervlak bereiken? Het antwoord is: door de Lorentzcontractie. Voor de waarnemer die met de muonen meebeweegt, lijken de aarde en haar atmosfeer heel snel te bewegen. Door de Lorentzcontractie lijkt de atmosfeer dus veel dunner. De muonen hoeven dus door een veel kleinere laag atmosfeer heen te bewegen, en zijn vanuit het oogpunt van de meebewegende waarnemer sneller op het aardoppervlak. In die kortere reistijd vervallen er minder muonen, en dit verklaart vanuit dit gezichtspunt waarom er zo veel op het aardoppervlak aankomen.

Wanneer we de twee verschijnselen van tijdsdilatatie en Lorentzcontractie vergelijken, ontstaat misschien de volgende verwarring. In diagrammen als afbeelding 1 lijken ruimte en tijd heel symmetrisch voor de komen. Hoe kan het dan dat tijdsintervallen tussen de tikken van bewegende klokken langer worden, maar lengtes van bewegende meetlatten korter? Het antwoord op deze vraag zien we in afbeelding 2. De lengte van een bewegende meetlat meten we op een vast tijdstip, bijvoorbeeld t=0. Die lengte kunnen we in de figuur dus aangeven door het lijnstuk AB. De tijdsintervallen tussen de tikken van de bewegende klok meten we echter op de plaatsen waar de klok op het moment van tikken is – de tijd tussen twee tikken komt dus bijvoorbeeld overeen met de “verticale verplaatsing” in het lijnstuk AC. We zien nu hoe de symmetrie gebroken is: in het geval van tijdsdilatatie meten we niet de tijd tussen twee gebeurtenissen op de plaats x=0, wat overeen zou komen met het lijnstuk AD. De tijd die overeenkomt met dat lijnstuk zou inderdaad korter dan 1 seconde, en dit resultaat is het volkomen symmetrische “tijdequivalent” van de Lorentzcontractie.

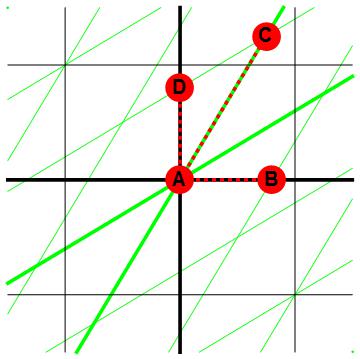
Afbeelding 2. Dilatatie vs. contractie.Om de Lorentzcontractie te bepalen meten we de afstand tussen A en B. Om de tijdsdilatatie te bepalen meten we de tijd tussen A en C. Het “tijdsymmetrische equivalent” voor het meten van de Lorentzcontractie zou het meten van de tijd tussen A en D zijn.

Een andere verwarring die het begrip Lorentzcontractie met zich meebrengt, is de zogenaamde ladderparadox. Stel dat een ladder, in de lengterichting, precies in een bepaalde schuur past. Nu gooien we de ladder met een enorme snelheid de schuur in. Vanuit de schuur gezien ondervindt de  bewegende ladder een Lorentzcontractie: de ladder moet nu dus gemakkelijk in de schuur passen. Maar vanuit de ladder gezien beweegt juist de schuur, en (alweer het relativiteitsbeginsel!) moet dus juist de schuur een Lorentzcontractie ondervinden. De schuur lijkt vanuit de ladder gezien kleiner, waardoor de ladder juist niet in de schuur zou moeten passen. We lijken op een vreemde tegenspraak te zijn gestuit – hoe lossen we deze paradox op?

De oplossing van deze paradox zien we in afbeelding 3. Het ruimtetijdpad van de schuur is hierin grijs aangegeven; het ruimtetijdpad van de ladder lichtgroen. (We hebben voor het gemak ook de achterdeur van de schuur open gezet, zodat de ladder door de schuur heen vliegt.) We zien dat op het tijdstip t=0 de ladder (het lijnstuk AB) inderdaad makkelijk in de schuur past. Maar… we zien dat op het tijdstip t’=0 de ladder (nu het lijnstuk AC) ruimschoots buiten de schuur uitsteekt! De oplossing van het probleem zit hem dus in het feit dat we niet over de “lengte” van een voorwerp kunnen spreken zonder te zeggen welke ruimte- en tijdrichtingen in de ruimtetijd we kiezen. De lengte van de ladder in het zwarte referentiekader wordt langs de horizontale ruimtelijnen gemeten; de lengte van de ladder in het groene referentiekader wordt langs de schuine ruimtelijnen gemeten. Er is dus geen tegenspraak wanneer de ene lengte niet overeenkomt met de andere – voor de ene waarnemer kan de ladder prima korter zijn dan de schuur, en voor de andere langer.

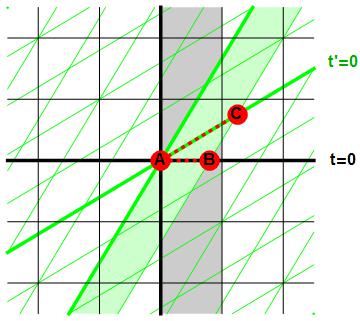
Afbeelding 3. De oplossing van de ladderparadox.Wanneer de zwarte waarneer het heeft over de lengte van de ladder, bedoelt hij het lijnstuk AB. Wanneer de groene waarnemer het heeft over de lengte van de ladder, bedoelt hij het lijnstuk AC.

Maar wat nu als we de achterdeur van de schuur dicht doen, en zodra (vanuit het zwarte perspectief gezien) de hele ladder in de schuur is de voordeur ook? De ladder zit dan in de schuur – en daarover zoude alle waarnemers het toch eens moeten zijn. Deze situatie is afgebeeld in afbeelding 4. Het moment waarop we de deur van de schuur dichtdoen is met de rode stip A aangegeven. Vanuit het zwarte perspectief is op dit moment de andere kant van de ladder nog niet bij de achtermuur van de schuur. Dit gebeurt pas iets later; de gebeurtenis die met de rode stip B is aangegeven. Maar tijd is zoals we gezien hebben in de relativiteitstheorie hebben een bijzonder begrip: de gebeurtenissen die voor de groene waarnemer gelijktijdig zijn met gebeurtenis B liggen op de schuine gestippelde groene lijn. Voor de groene waarnemer is dus op dit moment de achterkant van de ladder nog buiten de schuur (gebeurtenis C); die achterkant vliegt door totdat die bij gebeurtenis A, voor de groene waarnemer op een later tijdstip, ook de schuur in vliegt, en de schuur wordt dichtgedaan. Tussen gebeurtenis C en A in wordt de ladder dus samengedrukt: de voorkant staat al stil omdat die tegen de achtermuur is gebotst, maar de achterkant beweegt nog. Uiteindelijk komt de ladder, die eerst te lang was, zo dus ook voor de groene waarnemer in de schuur terecht. In de praktijk zal de ladder, die met een enorme snelheid tegen de achtermuur wordt geramd en ook nog eens flink wordt samengeperst, overigens ongetwijfeld in stukken uiteen spatten – maar met dat probleem hoeven we in een eenvoudig gedachte-experiment gelukkig geen rekening te houden.

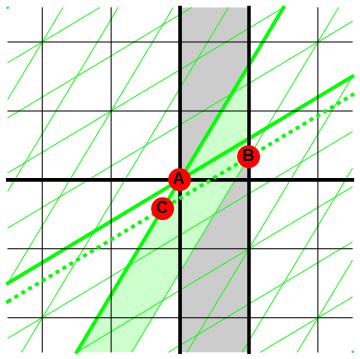
Afbeelding 4. De ladderparadox met een dichte achterdeur.De ladderparadox in het geval dat we de achterdeur van de schuur sluiten. Bij (A) sluiten we de deur. Bij (B) botst de ladder met de achterdeur van de schuur. Voor de zwarte waarnemer is dit ná (A); voor de groene waarnemer is het ervóór, en is de voorkant van de ladder nog buiten de schuur, bij (C).

We hebben nu zowel de tijdsdilatatie als de Lorentzcontractie uitgebreid bestudeerd. We hebben gezien dat deze tegenintuïtieve begrippen voor ons tot allerlei schijnbare paradoxen leiden, maar dat we met logisch redeneren al die paradoxen kunnen oplossen. In het volgende artikel in dit dossier kijken we naar nog een laatste beroemde paradox die de relativiteitstheorie lijkt op te leveren: de tweelingparadox.

Dit is het zevende artikel uit het dossier Relativiteitstheorie. In het achtste artikel komen we de beroemde tweelingparadox tegen, en zien we hoe die opgelost kan worden.

Afbeelding blokkenschema: Wikipedia-gebruiker Michiel1972.