Relativiteit (12): Zwarte gaten

Zwarte gaten zijn misschien wel de meest intrigerende toepassing van de algemene relativiteitstheorie. Eén van de redenen dat zwarte gaten zo interessant zijn, is dat ze relativistische en quantummechanische aspecten in zich verenigen. Op deze website verschijnt daarom naast de al aanwezige dossiers over relativiteitstheorie en quantummechanica ook een apart dossier over zwarte gaten. In dit artikel zullen we alleen kort de belangrijkste relativistische aspecten van zwarte gaten bespreken.

Een zwart gat is een plek in het heelal waar zich zoveel massa in zo’n kleine ruimte bevindt dat de zwaartekracht extreem groot wordt; zó groot, dat zelfs het licht niet aan die plek kan ontsnappen. Een dergelijke extreme concentratie van materie kan bijvoorbeeld ontstaan wanneer een zware ster al zijn brandstof verbruikt heeft en onder zijn eigen zwaartekracht is elkaar stort – een verschijnsel waarbij veel energie en licht vrijkomt, en dat we een supernova noemen. Ook in de kernen van veel sterrenstelsels bevindt zich zoveel massa dicht bij elkaar dat daar een zwart gat ontstaat.

Of een dergelijke concentratie van materie zó groot kan worden dat er geen licht aan kan ontsnappen, vroeg men zich al af lang voordat Einstein met zijn relativiteitstheorie op de proppen kwam. Zo schreef de geoloog John Michell in 1783 in een brief aan Henry Cavendish:

If the semi-diameter of a sphere of the same density as the Sun were to exceed that of the Sun in the proportion of 500 to 1, a body falling from an infinite height towards it would have acquired at its surface greater velocity than that of light, and consequently supposing light to be attracted by the same force in proportion to its vis inertiae, with other bodies, all light emitted from such a body would be made to return towards it by its own proper gravity.

Michell was bekend met het volgende fenomeen: om vanaf het oppervlak aan een massa-concentratie zoals een planeet of een ster te ontsnappen, zonder dat daarbij gebruik wordt gemaakt van een motor of andere hulpmiddelen, is een bepaalde minimumsnelheid nodig. Wordt een voorwerp met minder dan die snelheid omhoog afgeschoten, dan remt de zwaartekracht het voorwerp uiteindelijk voldoende af om het weer terug te laten vallen. Schieten we een voorwerp echter met deze minimumsnelheid of harder weg, dan verliest de zwaartekracht naarmate het voorwerp hoger komt dusdanig veel kracht dat het niet meer lukt om het voorwerp af te remmen. Het voorwerp ontsnapt dan aan de zwaartekracht van de planeet of ster. Deze snelheid wordt daarom de ontsnappingssnelheid genoemd.

Afbeelding 1. Een zwart gat.Een “artist impression” van een zwart gat dat een nabijgelegen ster opslokt. (Afbeelding: NASA.)

Het bijzondere van de ontsnappingssnelheid is, dat die niet afhangt van de massa van het voorwerp dat we wegschieten. Een zwaar voorwerp moeten we precies dezelfde snelheid geven als een licht voorwerp om het van bijvoorbeeld de aarde af te schieten. Een zwaar voorwerp wordt weliswaar harder teruggetrokken door de zwaartekracht van de aarde, maar het heeft door zijn grotere massa ook meer bewegingsenergie, waardoor het moeilijker af te remmen is. Deze effecten heffen elkaar precies op, zodat de uiteindelijke ontsnappingssnelheid gelijk is aan die van een licht voorwerp.

De ontsnappingssnelheid hangt echter wel af van de massa van de ster of planeet waarvandaan we het voorwerp wegschieten. Zo heeft de aarde een ontsnappingssnelheid van ongeveer 11,2 km/s, de planeet Jupiter van 59,5 km/s, en de zon van 617,5 km/s. Hoe zwaarder en dichter de concentratie van massa in het hemellichaam, hoe groter de ontsnappingssnelheid.

Michell was ook bekend met het feit dat licht met een eindige snelheid beweegt: de eerste snelheidmetingen van het licht dateren van het eind van de 17e eeuw. Hij vroeg zich daarom af: wat gebeurt er als we een hemellichaam tegenkomen waarvan de ontsnappingssnelheid groter is dan die van het licht? Kan het licht dan ook niet aan een dergelijk hemellichaam ontsnappen, en is het hemellichaam dus zwart?

In deze redering wordt natuurlijk een belangrijke aanname gemaakt: de aanname dat ook licht effecten van de zwaartekracht ondervindt. Dit was in de 18e eeuw nog allesbehalve duidelijk – dat werd het pas met de tests die Einsteins relativiteitstheorie bevestigden. Michell zegt dit ook expliciet: “…supposing light to be attracted by the same force in proportion to its vis inertiae, …”. Het feit dat het alles behalve duidelijk was of licht inderdaad door de zwaartekracht wordt aangetrokken (het is immers massaloos) zorgde ervoor dat de interesse in zwarte gaten vóór de opkomst van de relativiteitstheorie eigenlijk nooit erg groot werd. Daar kwam natuurlijk nog bij dat tot die tijd de lichtsnelheid “gewoon maar” een snelheid was. Pas met de komst van de relativiteit werd het duidelijk dat niets sneller kan gaan dan het licht, en dat het dus voor alles onmogelijk zou zijn om aan een zwart gat te ontsnappen.

Die laatste opmerking moeten we nog iets beter onder de loep nemen. De redenering aan de hand van een ontsnappingsnelheid geeft alleen het resultaat dat weggeschoten voorwerpen zonder motor of andere hulp niet aan een zwaar hemellichaam kunnen ontsnappen als de ontsnappingssnelheid groter is dan de lichtsnelheid. Maar wat gebeurt er als we met een motor proberen de afremming van de zwaartekracht tegen te werken? Of kunnen we bijvoorbeeld op een zwart gat een toren bouwen die zo hoog is dat op de top, waar de zwaartekracht kleiner is, de ontsnappingssnelheid wél kleiner is dan de lichtsnelheid?

Het antwoord op deze en soortgelijke vragen blijkt “nee” te zijn. Aan een relativistisch zwart gat kun je ook aan de hand van dit soort trucs niet ontsnappen. Om dit te kunnen begrijpen moeten we een zwart gat beschrijven op een manier die meer in de lijn van de relativiteitstheorie ligt.

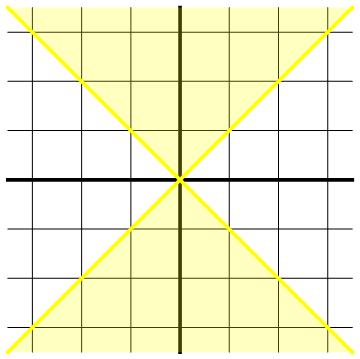
Afbeelding 2. Een lichtkegel.Een lichtkegel door de oorsprong: waarnemers en voorwerpen die door de oorsprong bewegen bevinden zich op elk tijdstip in het geel gekleurde gebied.

Laten we om te beginnen eens kijken naar afbeelding 2. We zien hier weer het gebruikelijke ruimtetijddiagram, met daarin in het geel de wereldlijnen van twee lichtflitsen aangegeven: een die van links naar rechts door de oorsprong beweegt, en een die van rechts naar links door datzelfde referentiepunt gaat. We weten inmiddels dat voorwerpen met massa niet sneller kunnen bewegen dan de lichtsnelheid. In het plaatje wil dat zeggen dat als die voorwerpen ook door de oorsprong komen, ze op elk ander tijdstip een afstand moeten hebben afgelegd die kleiner is dan de afstand die het licht op dat moment heeft afgelegd. Met andere woorden: de wereldlijnen van andere voorwerpen of waarnemers die door de oorsprong gaan liggen altijd tussen de twee gele lijnen.

Als we nog een tweede ruimtediemensie aan het diagram zouden toevoegen, zie afbeelding 3, zouden de twee lichtlijnen vervangen worden door een kegelvormig oppervlak. Het licht kan nu immers in alle richtingen in het tweedimensionale vlak bewegen. Als we een derde ruimtedimensie toevoegen wordt deze kegel een soortgelijke driedimensionale vorm in vier dimensies, al kunnen we die natuurlijk lastig tekenen. In al deze gevallen wordt het gebied in de ruimtetijd waarbuiten een door de oorsprong bewegende waarnemer niet kan komen de lichtkegel genoemd.

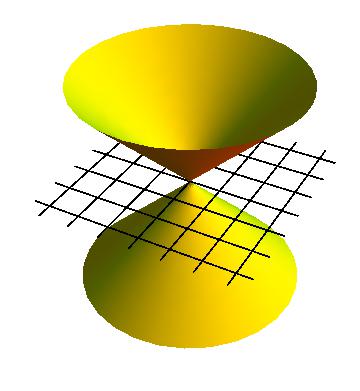
Afbeelding 3. Een lichtkegel voor een tweedimensionale ruimte.Het getekende horizontale raster bevat alleen de ruimtelijke x- en y-coördinaten; de tijd is zoals gebruikelijk in de verticale richting uitgezet. Waarnemers en voorwerpen die door de oorsprong bewegen, bevinden zich op elk moment binnen de lichtkegel.

Let op: de lichtkegel geeft aan waar een waarnemer niet kan komen in de ruimtetijd. Dat wil natuurlijk nog niet zeggen dat er plaatsen in de ruimte zijn waar de waarnemer niet kan komen. Bijvoorbeeld: ik kan niet over een halve seconde op de maan zijn, omdat ik dan sneller dan het licht zou moeten reizen. Het punt “op de maan, over een halve seconde” in de ruimtetijd is dus niet toegankelijk voor me. Dat wil niet zeggen dat ik niet op de maan kan komen: het ruimtetijdpunt “op de maan, over vijftig jaar” is bijvoorbeeld in principe best bereikbaar.

Elk punt in de ruimtetijd heeft zijn eigen lichtkegel, die de punten aangeeft die wel en niet bereikbaar zijn voor een waarnemer die zich op die tijd op die plaats bevindt. In afbeelding 4 zien we een schets van die verzameling van lichtkegels. De schets is natuurlijk sterk vereenvoudigd: in de praktijk zijn er oneindig veel lichtkegels – voor elk ruimtetijdpunt één – en zijn ze ook nog eens oneindig groot. We hebben in afbeelding 4 dus een klein stukje van een klein deel van de lichtkegels getekend.

Afbeelding 4. Lichtkegels in de ruimtetijd.Elk punt in de ruimtetijd heeft zijn eigen lichtkegel. Hier is van een aantal ruimtetijdpunten een deel van de lichtkegel getekend.

Afbeelding 4 geeft nog een vlakke ruimtetijd weer. Met andere woorden: dit is een situatie in de speciale relativiteitstheorie. Om zwarte gaten te beschrijven zijn we natuurlijk geïnteresseerd in de algemene relativiteitstheorie, omdat we daarmee ook de zwaartekracht kunnen beschrijven. In de algemene relativiteitstheorie kan ruimtetijd ook gekromd zijn. In dat geval kunnen naast elkaar liggende lichtkegels dus een beetje gedraaid zijn ten opzichte van elkaar. Het is wat lastig om dat op een gekromd oppervlak te tekenen, dus we maken in afbeelding 5 wederom een schets: we hebben hier de ruimtetijd nog steeds vlak afgebeeld, maar wel de lichtkegels “gebogen”. Het blijkt dat deze schets van een gekromde ruimtetijd voldoende nauwkeurig is om al te kunnen begrijpen hoe een zwart gat in de relativiteitstheorie werkt.

Afbeelding 5. Lichtkegels in een gekromde ruimtetijd.Aan de linkerkant van de afbeelding staan de lichtkegels vrijwel in dezelfde oriëntatie als in een vlakke ruimtetijd. Rechts in de afbeeldingen hellen de lichtkegels sterker naar rechts. Als gevolg daarvan zullen “stilstaande” voorwerpen rechts in de afbeelding langzaam naar rechts bewegen ten opzichte van “stilstaande” voorwerpen links. Met andere woorden: het is alsof zich rechts buiten de afbeelding een zwaar object bevindt dat massa aantrekt.

In afbeelding 6 schetsen we nogmaals een gekromde ruimtetijd, maar in dit geval is de kromming nog veel sterker: in het midden van de afbeelding is de ruimtetijd zo sterk gekromd dat de lichtkegels van beide kanten af volledig op hun kant komen te liggen. De (zwarte) lijn waarop dit gebeurt wordt een singulariteit genoemd. Wie zich in een ruimtetijdpunt vlak bij de singulariteit bevindt kan maar één kant op: naar de singulariteit toe. Dit is dan ook de schetsmatige weergave van een relativistisch zwart gat: we hebben hier een zodanig sterk gekromde ruimte (natuurlijk veroorzaakt door een zware massaconcentratie) dat het niet meer mogelijk is om ervandaan te bewegen.

Afbeelding 6. Een zwart gat.Een schets van de lichtkegels rond een zwart gat. De zwarte lijn geeft de wereldlijn van de singulariteit weer; de rode lijnen de ruimtetijdpunten waarvandaan het zelfs met de lichtsnelheid niet meer mogelijk is om de singulariteit te ontwijken.

Twee bijzondere ruimtetijdlijnen in afbeelding 6 zijn in het rood aangegeven. In afbeelding 7 zien we een gebiedje rond de linker rode lijn uitvergroot weergegeven. Wat we zien is dat rechts van deze lijn de lichtkegels verder dan 45 graden gekanteld zijn. Dit betekent voor de waarnemer die zich binnen deze lijnen bevindt dat hij alleen maar naar binnen toe kan bewegen: hoe snel hij ook probeert naar buiten te bewegen, hij zal altijd naar binnen gezogen worden. Een waarnemer die zich net buiten de groene lijnen bevindt kan zich, als hij heel hard zijn best doet, nog net aan het zwarte gat onttrekken. Hij moet daarvoor met een enorme snelheid van bijna de lichtsnelheid naar buiten bewegen. Kortom: de rode lijnen geven de locatie aan waar de relativistische ontsnappingssnelheid precies gelijk is aan de lichtsnelheid. Daarbuiten kan een waarnemer  nog ontsnappen; daarbinnen niet. De straal van het gebied binnen de groene lijnen kunnen we dus zien als de “grootte” van het zwarte gat; die grootte wordt de Schwardzschildstraal genoemd.

Afbeelding 7. De Schwardzschildstraal.Een uitvergrote versie van het gebied tussen de linker rode lijn en de zwarte lijn in afbeelding 6.

Hiermee hebben we dus een echt, relativistisch zwart gat beschreven. We zien nu ook dat alle trucs die we eerder bedachten om aan een zwart gat te ontsnappen niet werken: wie zich eenmaal binnen de Schwardzschildstraal bevindt wordt zo hard “naar binnen gezogen” dat hij zelfs als hij met de lichtsnelheid beweegt, niet meer naar buiten komt. Een relativistisch zwart gat is dus écht zwart!

Door de sterke kromming van de ruimtetijd vinden in en rond een zwart allerlei interessante relativistische verschijnselen plaats. Zo kunnen we, op een soortgelijke manier als voor de tijdsdilatatie, laten zien dat op de rand van een zwart gat de tijd – gezien vanuit een ver verwijderde waarnemer – extreem langzaam gaat lopen; op de Schwardzschildstraal zelf lijkt die tijd voor een externe waarnemer zelfs tot stilstand te komen. Wie zelf in het zwarte gat valt merkt daar natuurlijk niets van. Net als in het geval van tijdsdilatatie ziet zo’n waarnemer zijn eigen klok gewoon eenmaal per seconde tikken. Hij zal dus ook niet merken dat hij de Schwardzschildstraal passeert; de ruimte ziet er daar voor een invallende waarnemer precies hetzelfde uit als in de rest van het heelal. Om ongemerkte opsluiting te voorkomen is het dus maar beter om niet te dicht in de buurt van zwarte gaten te komen!

De relativiteitstheorie geeft maar één kant van het verhaal van zwarte gaten. Echt interessant wordt het als we ook de effecten van de quantummechanica (zie het aparte dossier daarover dat half januari 2015 verschijnt) in het verhaal meenemen. Dan blijkt bijvoorbeeld dat het op subtiele wijze toch mogelijk is om heel langzaam materie aan een zwart gat te laten ontsnappen – de zogenoemde Hawkingstraling. Verder is het dan nog maar de vraag of een waarnemer inderdaad niets merkt als hij de Schwarzschildstraal passeert, of dat hij terecht komt in een hete brij van materie die een firewall genoemd wordt. Op veel van dit soort vragen is het antwoord overigens nog niet bekend, omdat het combineren van de relativiteitstheorie en de quantummechanica voor een groot deel nog een open vraagstuk in de theoretische natuurkunde is. Zie voor meer over dit vraagstuk bijvoorbeeld het artikel over snaartheorie dat op deze website zal verschijnen. Ook experimenteel is er erg weinig over zwarte gaten bekend, om de simpele reden dat we ze niet in het laboratorium kunnen maken, en niet of nauwelijks (ze zijn immers zwart!) aan de hemel kunnen waarnemen. Zoals gezegd: al deze aspecten van zwarte gaten komen t.z.t. in het aparte dossier over deze objecten nader aan bod.

Dit is het twaalfde en voorlopig laatste artikel uit het dossier Relativiteitstheorie. Op dinsdag 13 januari verschijnt het eerste artikel in een nieuw dossier: dat over quantummechanica.