Snaren en holografie (9): AdS/CFT

In dit artikel:

• Een veelbesproken artikel
• AdS/CFT
• AdS
• CFT
• Het holografisch principe

Afbeelding 1. Een hyperbolische ruimte.Hyperbolische ruimtes zijn de ’tijdloze’ variant van anti-de Sitterruimtes – de ruimtetijdvormen waarvoor de ‘AdS’ in ‘AdS/CFT’ staat. We zullen in dit artikel zien welke belangrijke rol dergelijke ruimtes in de snaartheorie spelen. In bovenstaande afbeelding zien we een tweedimensionale projectie van een driedimensionale hyperbolische ruimte. Afbeelding: Wikipedia-gebruiker Tomruen.

Een veelbesproken artikel

Op 28 november 1997 verscheen op het internet een voorpublicatie van een artikel van de Argentijnse theoretisch natuurkundige Juan Maldacena, met als titel The large N limit of superconformal field theories and supergravity. Het voorpubliceren van artikelen op het internet is tegenwoordig heel gebruikelijk in de theoretische natuurkunde: vrijwel elk artikel verschijnt eerst in een elektronische versie op de website arxiv.org, en doorloopt daarna pas het gebruikelijke review-proces bij een papieren tijdschrift.

Dat laatste gebeurde ook met het artikel van Maldacena, dat uiteindelijk in 1998 in het tijdschrift Advances in Theoretical and Mathematical Physics verscheen. Voordat het artikel officieel gepubliceerd werd, was het echter al tientallen keren geciteerd. Op dit moment is dat opgelopen tot ruim 11.000 keer, waarmee het artikel ruimschoots op de eerste plaats staat op de lijst van meest geciteerde artikelen in de theoretische hoge-energiefysica. Naar het artikel op de tweede plaats, een artikel uit 1967 van de Nobelprijswinnaar Steven Weinberg, zijn zo’n 8000 verwijzingen in andere publicaties.

Naar boven

AdS/CFT

Waarom het artikel van Maldacena zo immens populair werd, zullen we in dit artikel en het volgende zien. Het idee van Maldacena klinkt in eerste instantie niet eens zo heel erg bijzonder: hij toonde het bestaan van een nieuwe dualiteit aan. Daarmee was hij lang niet de eerste. Het hoogtepunt van de intensieve zoektocht naar de dualiteiten die snaartheorieën met elkaar verbinden, was in 1998 al achter de rug. Maldacena’s dualiteit was echter geen dualiteit tussen twee snaarmodellen, maar een dualiteit tussen een snaarmodel en een model van ‘ouderwetse’ puntdeeltjes. Daarnaast verbond de dualiteit twee modellen die, zoals we in dit artikel zullen zien, in twee heel belangrijke verdere opzichten van elkaar verschilden.

Het systeem dat Maldacena bestudeerde was het volgende. Hij bekeek een type IIB-snaarmodel, waarin zoals we hebben ontdekt ook D-branen (met een oneven aantal ruimtedimensies) kunnen voorkomen. In zijn model nam Maldacena een aantal driedimensionale D-branen op. Deze D3-branen liggen bovenop elkaar: er is dus in zekere zin sprake van één ‘dikke’ D-braan. Het precieze aantal D3-branen kan daarbij willekeurig gekozen worden: de ‘N’ in de titel van het artikel van Maldacena staat voor het aantal D-branen.

Zoals we ook in het artikel over D-branen hebben gezien, kunnen deze objecten op twee manieren worden beschreven. Ten eerste kunnen we ze zien als hogerdimensionale objecten waarop open snaren eindigen. Ten tweede kunnen we ze beschrijven als hogerdimensionale versies van zwarte gaten. Het model van Maldacena kan vanuit het perspectief van de snaren zelf daarom ook op twee verschillende manieren worden opgebouwd. Het kan allereerst beschreven worden als een theorie van open snaren die op de D3-branen eindigen. Aan die theorie moeten dan vanwege consistentie-eisen ook gesloten snaren worden toegevoegd die van de D-branen af kunnen bewegen als ze ontstaan bij botsingen van open snaren. Omgekeerd kunnen we het model zien als een theorie van gesloten snaren die bewegen rond een driedimensionale zwarte p-braan – de hogerdimensionale versie van een zwart gat. In deze beschrijving zijn juist de open snaren secundair: ze ontstaan als de gesloten snaren de p-braan bereiken en openbreken om op de p-braan te kunnen eindigen.

Afbeelding 2. Juan Maldacena.Het artikel van Maldacena uit 1997 (gepubliceerd in 1998) wordt gezien als een grote doorbraak in de theorie van de quantumzwaartekracht. Foto: Institute for Advanced Study, Princeton.

In dit model maakte Maldacena vervolgens het aantal D3-branen (N) groter en groter. Daardoor wordt het zwarte gat steeds dieper en dieper, en verwijdert de horizon, waar veel van de gesloten snaren zich bevinden, zich steeds verder van de D3-branen, waar de open snaren zich bevinden. Met andere woorden: de twee versies van het model beschrijven oorspronkelijk exact dezelfde natuurkunde, maar uiteindelijk wordt de ene beschrijving een theorie van alleen gesloten snaren rond de horizon, die de open snaren diep in het zwarte gat niet meer ‘zien’, terwijl de andere beschrijving juist een theorie wordt van alleen open snaren op de D3-branen, die de gesloten snaren ver weg rond de horizon niet meer zien. Maldacena’s argument was nu het volgende: aangezien de modellen waar we mee beginnen exact hetzelfde zijn, zouden ook de modellen waar we mee eindigen duaal aan elkaar moeten zijn. Met andere woorden: hij had een dualiteit gevonden tussen een theorie van alleen gesloten snaren en een theorie van alleen open snaren.

De oplettende lezer vraagt zich misschien af hoe het nu mogelijk is dat één van de twee modellen een theorie van alleen open snaren is. Hebben we niet eerder gezien dat bij botsingen in zo’n model altijd ook gesloten snaren gevormd moeten kunnen worden? Dat is inderdaad waar, maar het blijkt dat er in de limiet die Maldacena bestudeerde nog iets bijzonders gebeurt. De open snaren worden in het proces waarbij N steeds groter wordt gemaakt namelijk ook steeds korter. Uiteindelijk worden ze zo kort dat we niet meer over snaren kunnen spreken: de theorie in de buurt van de D3-branen is aan het eind van dit proces een theorie van puntdeeltjes geworden!

De dualiteit van Maldacena staat tegenwoordig bekend als de AdS/CFT-correspondentie. Laten we om die naam te begrijpen iets beter kijken naar de twee duale theorieën die Maldacena in zijn artikel beschreef.

Naar boven

AdS

Doordat het zwarte gat (of eigenlijk: de zwarte p-braan) in de limiet van Maldacena steeds zwaarder wordt, gaat het gebied waar de gesloten snaren zich bevinden zich steeds meer concentreren rond de horizon van het zwarte gat. Om goed te beschrijven wat daar gebeurt, moeten we tijdens het groter maken van N daarom ook steeds meer inzoomen op het gebied rond de horizon. De vraag is: welke ‘vorm’ heeft het heelal waarin de gesloten snaren zich na dit inzoomen bevinden?

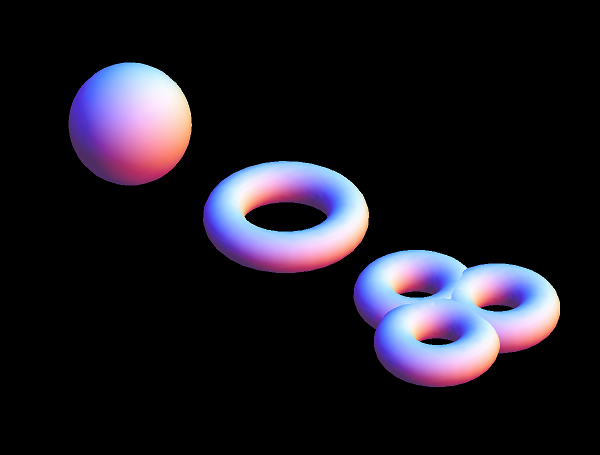
Afbeelding 3. Gekromde tweedimensionale oppervlakken.Van de drie hierboven getekende oppervlakken heeft alleen de bol op elk punt een even grote kromming.

Van tweedimensionale oppervlakken zijn we gewend dat ze gekromd kunnen zijn – zie afbeelding 3. Precies hetzelfde geldt voor de tiendimensionale ruimtetijd waarin snaren zich bewegen, al is het afbeelden of zelfs het voorstellen van tiendimensionale kromming natuurlijk veel lastiger. Wie de artikelenserie over relativiteitstheorie heeft gelezen, weet ook wat kromming in de ruimtetijd betekent: de gebogen banen die objecten door die kromming afleggen, ervaren wij als afbuiging door zwaartekracht. Rond de horizon van een zwart gat verwachten we natuurlijk een sterke zwaartekracht, en dus ligt het voor de hand dat de tiendimensionale ruimtetijd waarin de gesloten snaren zich bevinden ook gekromd is.

Nu is de ruimte rond de horizon van een zwarte p-braan helemaal leeg, en is er weinig reden waarom de kromming op de ene plaats anders zou zijn dan die op een andere. We kunnen ons nog voorstellen dat de kromming op verschillende afstanden van de p-braan verschillend is, maar juist door het inzoom-proces op de horizon gaat ook dat effect verloren. Alle punten waarop we inzoomen liggen op vrijwel dezelfde afstand van de p-braan. We verwachten dus dat de kromming van de tiendimensionale ruimtetijd waar de gesloten snaren doorheen bewegen overal hetzelfde is.

Van de tweedimensionale figuren in afbeelding 3 is er maar één waarvan de kromming op elk punt even groot is: dat is de bol linksboven. Naast de bol blijken er nog twee tweedimensionale vormen te bestaan die overal dezelfde kromming hebben. De eerste is een plat vlak: dat heeft helemaal geen kromming. Een wat ingewikkelder vorm is het hyperbolische vlak. Deze tweedimensionale vorm is lastiger te tekenen, aangezien we die niet zonder vervormingen in drie dimensies kunnen weergeven. De best mogelijke ‘afbeelding’ van het hyperbolische vlak kunnen we maken door het vlak te vullen met even grote ’tegels’, en vervolgens die tegels zo te vervormen dat ze wel in het platte vlak passen. De graficus M. C. Escher was hier een meester in – zie bijvoorbeeld deze prent. In afbeelding 4 hieronder zien we een soortgelijke afbeelding. Het vlak is gevuld met oneindig veel tegels in de vorm van een driehoek. Om het ‘echte’ hyperbolische vlak terug te krijgen zouden we deze afbeelding zo moeten vervormen dat alle tegels weer even groot worden – iets dat zoals gezegd in drie dimensies niet mogelijk is.

Afbeelding 4. Het hyperbolische vlak.Een hyperbolisch vlak vormgetrouw afbeelden in twee of drie dimensies is onmogelijk. Hier is het vlak gevuld met even grote tegels, die vervolgens zo vervormd zijn dat ze in het tweedimensionale vlak passen. Afbeelding: Anton Sherwood.

Ook voor andere aantallen dimensies dan twee kan wiskundig bewezen worden dat er maar drie ‘basisvormen’ zijn die overal dezelfde kromming hebben: de hogerdimensionale versies van de bol (in d dimensies aangegeven met S^d), het platte vlak (meestal R^d genoemd) en de hyperbolische ruimte (H^d). Deze basisvormen kunnen natuurlijk ook gecombineerd worden: we zouden van een vijfdimensionale ruimte bijvoorbeeld twee dimensies kunnen krommen op een bol, en de overige drie op een hyperbolische driedimensionale ruimte. In korte notatie geven we dit weer als S² × H³.

We hebben het nu gehad over ruimtes, maar de gesloten snaren bevinden zich in de ruimtetijd, die naast alle ruimtedimensies ook een tijddimensie bevat. Ook ruimtetijd kan op elk punt en op elk moment hetzelfde gekromd zijn. Ook dit blijkt weer op drie manieren te kunnen, die sterk overeenkomen met de drie manieren waarop we ruimtes kunnen krommen. De ruimtetijd-variant van de gekromde bol staat bekend als de de Sitterruimte (het woord ’tijd’ wordt, enigszins verwarrend, in de naam meestal weggelaten) en in d ruimtetijddimensies aangegeven als dS_d. De Nederlandse astronoom en wiskundige Willem de Sitter bestuurde rond 1920 als eerste heelalmodellen die deze vorm hebben. Ook een vlakke ruimtetijd, meestal genoteerd als M_d, is natuurlijk een optie. Ten slotte is er het ruimtetijd-equivalent van de hyperbolische ruimte, die (omdat de wiskundige beschrijving ervan slechts met een minteken verschilt van de de Sitterruimte) de anti-de Sitterruimte, of AdS_d, wordt genoemd.

Afbeelding 5. Willem de Sitter.De Sitter (1872-1934) onderzocht rond 1920 heelalmodellen met een constante ruimtetijdkromming. Foto: Yerkes Observatory, University of Chicago.

Welke van al deze ruimtes en ruimtetijden met constante kromming komen nu voor in de tiendimensionale ruimtetijd waarin de gesloten snaren rond de horizon van de p-braan bewegen? Na wat rekenwerk blijkt dat de drie ruimtedimensies parallel aan de p-braan plus de dimensie die recht vanaf deze p-braan naar buiten loopt, samen met de tijddimensie een vijfdimensionale anti-de Sitterruimte vormen. De overige vijf dimensies krommen zich tot een vijfdimensionale bol. In de ingevoerde korte notatie: de uiteindelijke ruimtetijd is van de vorm AdS₅ × S⁵. Omdat de vijfdimensionale bol in de rest van het verhaal een vrij eenvoudige rol speelt, komt alleen de anti-de Sitterruimte voor in de naam ‘AdS/CFT-correspondentie’.

Naar boven

CFT

Hoe zit het met het andere van de twee duale modellen? Zoals we hierboven hebben besproken, is dit een theorie van puntdeeltjes die zich in de vier ruimtetijddimensies van de D3-branen bewegen. Het bijzondere aan dit model is dat de D3-branen zich diep binnen het zwarte gat bevinden en volledig vlak zijn. Het feit dat de D3-branen niet gekromd zijn, betekent dat in deze theorie de zwaartekracht (die immers de kromming van de ruimtetijd beschrijft) geen enkele rol speelt. Dit kunnen we ook zien aan het feit dat dit model geen gesloten snaren meer bevat: het waren immers de gesloten snaren waarmee het zwaartekrachtsdeeltje beschreven kon worden.

De relativiteitstheorie speelt in de vierdimensionale theorie dus geen enkele rol weer, maar de quantummechanica doet dat wel. Bij nadere bestudering blijkt het model dat de puntdeeltjes in de D3-branen beschrijft, een quantumveldentheorie te zijn, die bekend staat onder de naam ‘vierdimensionale maximaal supersymmetrische Yang-Millstheorie’. Dergelijke theorieën werden in 1954 voor het eerst grondig bestudeerd door de fysici Chen Ning Yang en Robert Mills. Uit de naam zien we dat de theorie ook supersymmetrisch is, en dus bijvoorbeeld even veel soorten bosonische deeltjes als fermionische deeltjes bevat.

Wat niet uit de naamgeving blijkt, is dat deze Yang-Milsstheorie nog veel meer symmetrieën heeft dan alleen supersymmetrie. Een symmetrie (zie dit artikel voor meer informatie) is een transformatie die we op een natuurkundig systeem kunnen toepassen, zodanig dat het resulterende systeem ook aan alle natuurwetten voldoet. Een bekend voorbeeld is verschuiving of translatie: als we een willekeurig natuurkundig systeem een meter naar links of rechts verschuiven, voldoet het nog altijd aan de natuurwetten.

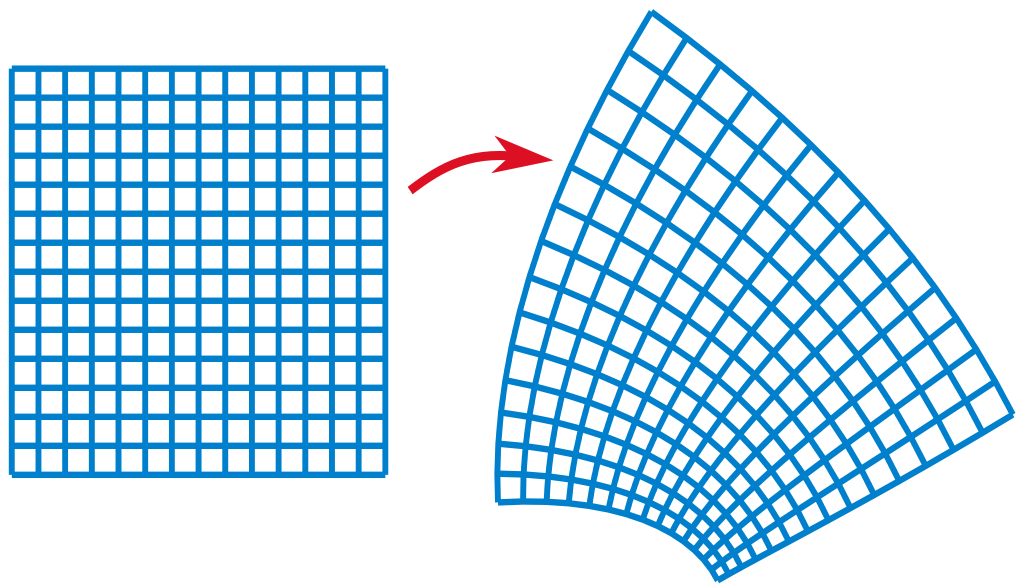
Afbeelding 6. Een voorbeeld van een conforme transformatie.In deze vervorming veranderen hoeken niet: merk op dat de lijnen in de rechterafbeelding nog steeds overal loodrecht op elkaar staan. Afbeelding: Oleg Alexandrov.

Translatiesymmetrie is dus een symmetrie die ook in onze vierdimensionale natuur aanwezig is, maar de Yang-Millstheorie die in de AdS/CFT-correspondentie voorkomt, heeft nog allerlei symmetrieën die we uit ons dagelijks leven niet kennen. Het blijkt dat we in deze theorie een willekeurig systeem namelijk kunnen vervormen, zolang we dat maar op zo’n manier doen dat alle hoeken in het systeem hetzelfde blijven. Afstanden hoeven daarbij niet hetzelfde te blijven – zie afbeelding 6 voor een voorbeeld. Het moge duidelijk zijn dat deze vervorming geen symmetrie is in onze eigen natuur: een bal die in de linkerfiguur in afbeelding 6 over een rechte lijn rolt (iets wat alle ballen waarop geen krachten werken doen), rolt in de rechterfiguur over een vreemde kromme lijn – een baan die niet aan de natuurwetten van rollende ballen zonder externe krachten voldoet.

De maximaal supersymmetrische Yang-Millstheorie heeft deze vreemde symmetrie echter wel. Elke transformatie waarbij hoeken niet veranderen, is dus een symmetrie, en vanwege het niet veranderen van hoeken (en dus plaatselijk niet vervormen) wordt een quantumveldentheorie waarvoor dit geldt een conforme veldentheorie genoemd. De Engelse term, conformal field theory, wordt afgekort met CFT, waarmee de andere helft van de kreet ‘AdS/CFT-correspondentie’ verklaard is.

Naar boven

Het holografisch principe

Samenvattend: Juan Maldacena liet in zijn baanbrekende artikel zien dat er een dualiteit is tussen een vierdimensionale conforme veldentheorie en een theorie van gesloten snaren in een tiendimensionale AdS₅ × S⁵-ruimtetijd. Dat deze dualiteit zo bijzonder is, volgt uit twee eigenschappen. Ten eerste is de dualiteit een dualiteit tussen een model mét zwaartekracht (de theorie van gesloten snaren) en een model zónder zwaartekracht (de conforme veldentheorie). Dat maakt de dualiteit erg geschikt om het probleem van de quantumzwaartekracht beter te begrijpen: er kunnen nu immers ‘vertalingen’ gemaakt worden vanuit de snaartheorie naar een veel beter begrepen ‘gewone’ quantumveldentheorie waarin de zwaartekracht niet voorkomt.

Ten tweede hebben de twee duale theorieën een heel verschillend aantal dimensies. De conforme veldentheorie speelt zich af in vier ruimtetijddimensies; de gesloten-snaartheorie in de gebruikelijke tien. Het feit dat er dualiteiten kunnen bestaan tussen theorieën in een verschillend aantal dimensies was iets dat al sinds de jaren ’70 vermoed werd op basis van berekeningen aan zwarte gaten. Dit vermoeden was bekend komen te staan onder de naam ‘holografisch principe’ – naar analogie van een hologram, waarin een driedimensionale afbeelding wordt weergegeven in twee dimensies. Tot het artikel van Maldacena was het echter nog nooit gelukt om een overtuigend voorbeeld van het holografisch principe te geven. De AdS/CFT-correspondentie bracht daarin verandering. Om goed te begrijpen waarom dit zo’n grote doorbraak betekende, gaan we in het komende artikel dieper in op de belangrijke rol van het holografisch principe in de theorie van de quantumzwaartekracht.

Naar boven

Een deel van de afbeeldingen uit dit artikel is eerder gepubliceerd in het boek ‘Snaartheorie‘ van de auteur.

In het tiende artikel in dit dossier zullen we zien hoe de AdS/CFT-dualiteit een voorbeeld vormt van een al veel eerder vermoed verband: het holografisch principe.