Snaren en holografie (4): Snaartheorie

In dit artikel:

• Van snaren naar quantumzwaartekracht
• Anomalieën
• Waarom werkt de snaartheorie?
• Open en gesloten snaren

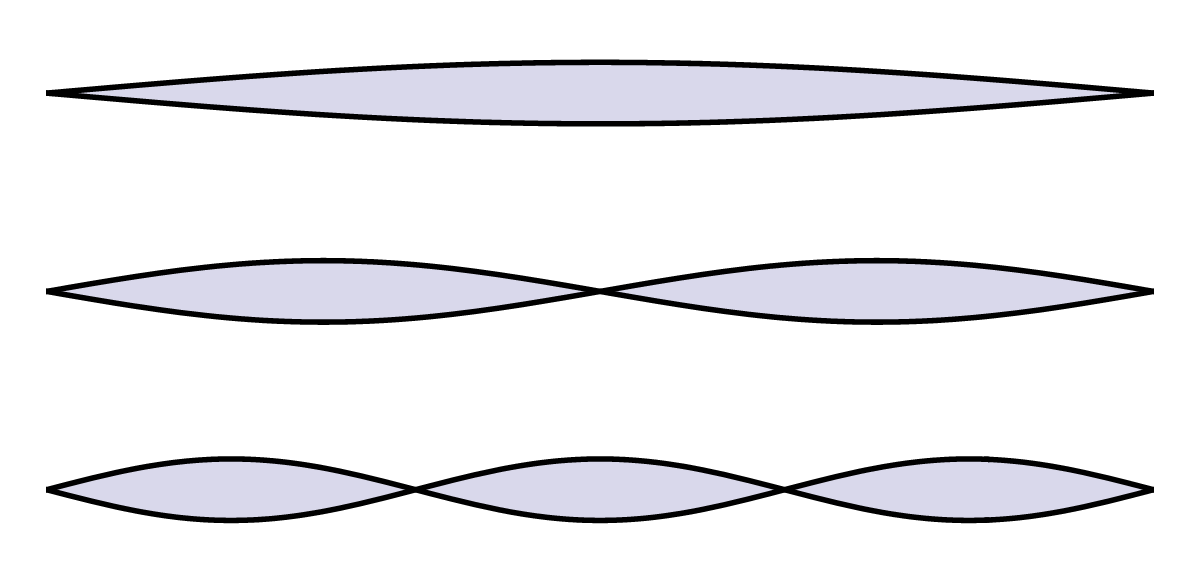
Afbeelding 1. Trillingen in snaren.Net als snaren in de muziek kunnen ook fundamentele snaren op verschillende manieren trillen. De ‘grondtoon’ (boven) stelt het lichtst mogelijke deeltje voor; de boventonen (midden en onder) de zwaardere deeltjes. Overigens zijn voor het tekengemak hier open snaren (met twee eindpunten) getekend, maar precies hetzelfde geldt voor lusvormige, gesloten snaren. (Zie de eerste afbeelding van het vorige artikel voor een voorbeeld van een trilling in zo’n gesloten snaar.)

Van snaren naar quantumzwaartekracht

Het zou nog vier jaar duren voor de formule van Veneziano weer in de belangstelling zou komen. Net als de snaren die in muziekinstrumenten gebruikt worden, kunnen ook de fundamentele snaren die de formule van Veneziano beschreef, trillen. In muziekinstrumenten veroorzaken de verschillende trillingen van een snaar verschillende tonen – zie afbeelding 1. De eenvoudigste trilling geeft een toon die de grondtoon van de snaar wordt genoemd. Trillingen waarbij meer golflengtes op een snaar passen, geven de hogere boventonen. De verschillende trillingen in Veneziano’s microscopische snaren hebben ook elk een eigen interpretatie: die van verschillende deeltjes. Zo geeft het trillen de snaar bijvoorbeeld meer energie, en volgens Einsteins beroemde formule E=mc² betekent meer energie (E) ook dat de snaar meer massa (m) zal hebben. Wanneer we uitzoomen naar onze alledaagse afstandsschalen zien we verschillende trillende snaren daardoor als vrijwel puntvormige deeltjes die elk een verschillende massa hebben. Met andere woorden: met één type snaar kan een heel scala aan ‘klassieke’ deeltjes beschreven worden!

In 1974 viel het de Fransman Joël Scherk en de Amerikaan John Schwarz op dat een van de trillingsvormen van de fundamentele snaar een heel speciaal deeltje beschreef: een deeltje met alle eigenschappen van het graviton – het deeltje dat de zwaartekracht overbrengt. Het probleem van het beschrijven van de quantumzwaartekracht stond op dat moment volop in de belangstelling, en dus lag het voor de hand dat Scherk en Schwarz zich afvroegen of de snaartheorie niet een heel andere interpretatie kon krijgen dan die van een theorie voor de sterke kernkracht. Zou het mogelijk zijn om met de snaartheorie de quantumzwaartekracht te beschrijven?

Om dat mogelijk te maken, hoefde in eerste instantie maar een kleine aanpassing gedaan te worden. Om de sterke kernkracht te beschrijven, zouden de fundamentele snaren zo’n 10^-15 meter lang moeten zijn – grofweg duizend keer zo groot als de kleinst mogelijke afstand waarop fysici op dit moment met deeltjesversnellers kunnen ‘kijken’. Om de zwaartekracht te beschrijven moesten diezelfde snaren echter nog veel kleiner zijn: zo’n 10^-35 meter lang! Het leek vooralsnog onmogelijk om experimenten bij dergelijke afstandsschalen te doen: daarvoor zou een deeltjesversneller ter grootte van het hele zonnestelsel nodig zijn. Toch was het natuurlijk interessant om de theoretische gevolgen van het idee van Scherk en Schwarz te onderzoeken. Helaas liep men daarbij al snel tegen een probleem aan dat de snaartheorie wederom voor de nodige jaren van het strijdtoneel deed verdwijnen.

Afbeelding 2. John Schwarz.John Schwarz stelde in 1974 samen met Joël Scherk voor dat quantumsnaren wel eens de zwaartekracht zouden kunnen beschrijven. In 1984 ontdekte hij vervolgens samen met Michael Green hoe een dergelijke snaartheorie anomalievrij gemaakt kon worden. Foto: Bob Paz.

Naar boven

Anomalieën

De quantumfysica is een wiskundig gecompliceerde theorie waarin het niet altijd meevalt om in de berekeningen de uitkomst ‘oneindig’ te vermijden. We zagen daar in het vorige artikel al een voorbeeld van, toen we beschreven hoe de renormalisatieprocedure nodig was om oneindigheden in de berekeningen voor de elektromagnetische kracht en de sterke en zwakke kernkracht te vermijden. Een ander voorbeeld van een ongewenste oneindigheid in de quantumfysica is dat van een anomalie. Vrijwel alle natuurkundige theorieën hebben bepaalde symmetrieën: een voorbeeld is de ’translatiesymmetrie’ die zegt dat elk experiment dat we op een bepaalde plaats in een verder lege ruimte uitvoeren, dezelfde uitkomst moet geven als we het experiment een meter naar links, rechts, boven of beneden verplaatsen.

Nu is het in de quantumfysica soms zo dat een theorie op grote schaal een bepaalde symmetrie heeft, maar dat specifieke interactieprocessen deze symmetrie op de allerkleinste schaal niet blijken te hebben. Vaak betekent het bestaan van zo’n anomalie dat de theorie de verschijnselen die we proberen te beschrijven toch niet helemaal nauwkeurig beschrijft. Dat probleem uit zich vervolgens in de quantumtheorie in het verschijnen van oneindig grote uitkomsten in bepaalde berekeningen. Aangezien het heel specifieke berekeningen aan bepaalde interactieprocessen zijn die tot deze oneindigheden leiden, worden dergelijke oneindigheden ‘anomalieën’ genoemd.

Ook de snaar-zwaartekracht die Scherk en Schwarz in 1974 hadden voorgesteld, bleek tot bepaalde anomalieën te leiden. De oneindigheden leken al snel een onoverkomelijk probleem, en de snaartheorie overkwam wat haar al een paar keer eerder was overkomen: ze verdween in de ijskast. Enkele fysici (waaronder Scherk – die enkele jaren later op jonge leeftijd overleed – en Schwarz zelf) waren echter zo onder de indruk van het idee dat ze in de daaropvolgende jaren toch bleven zoeken naar een manier om de theorie te ‘redden’. Uiteindelijk was het John Schwarz zelf die samen met de Engelsman Michael Green een oplossing voor het anomalieprobleem vond. Dat gebeurde in 1984 – tien jaar na het verschijnen van het artikel van Scherk en Schwarz. Green en Schwarz pasten de manier waarom de snaren op het microscopische niveau met elkaar wisselwerken in de theorie een heel klein beetje aan, en deze wiskundige ingreep (waarvan de details helaas wat te ver gaan om die hier te beschrijven) bleek voldoende om de snaartheorie niet alleen op grote maar ook op kleine schaal alle gewenste symmetrieën te geven. De oneindigheden waren als sneeuw voor de zon verdwenen, en de snaartheorie was back in business!

Naar boven

Waarom werkt de snaartheorie?

De vondst van Green en Schwarz zou later bekend komen te staan als de ‘eerste snaartheorie-revolutie’. (De tweede revolutie zullen we in het volgende artikel tegenkomen.) Waar tot 1984 slechts een handjevol fysici aan quantumsnaren werkte, maakte het verwijderen van de anomalieën in de theorie haar in één klap veel interessanter voor theoretisch natuurkundigen. Het duurde niet lang voordat vrijwel elke zichzelf respecterende universiteit een groep theoretisch fysici had die aan de snaartheorie werkte, en er wereldwijd vele honderden fysici het onderwerp onderzochten. De hoop was dat het oude probleem van de quantumzwaartekracht door middel van de snaartheorie nu snel opgelost kon worden, en dat de snaartheorie daarmee zelfs een ’theorie van alles’ (dat wil zeggen: een beschrijving van alle bekende natuurkrachten en deeltjes) zou vormen. Nu, dertig jaar later, is gebleken dat het optimisme in die tijd misschien wel érg groot was. Het probleem van de quantumzwaartekracht is immers nog altijd niet volledig opgelost. Toch heeft de snaartheorie ons heel veel geleerd – niet alleen over een mogelijke oplossing van het quantumzwaartekrachtsprobleem, maar mogelijk nog belangrijker: over het probleem zelf. Het holografisch principe dat we in dit dossier beschrijven, is misschien wel het belangrijkste voorbeeld van zo’n algemene les over quantumzwaartekracht die de snaartheorie ons geleerd heeft.

Maar waarom doet de zwaartekracht eigenlijk wat ze doet? Hoe kon het dat het onoplosbaar lijkende probleem van de renormalisatie van quantumzwaartekracht door de snaartheorie ineens opgelost werd? Het antwoord is – met de kennis van achteraf – eigenlijk heel voor de hand liggend. Zie afbeelding 3: de linkerhelft van deze afbeelding zagen we ook in het vorige artikel. Daar legden we uit dat het grote probleem van de quantumzwaartekracht is dat interacties (hier tussen een elektron en een zwaartekrachtsdeeltje, het graviton) plaatsvinden in een punt. Zo’n punt heeft een grootte van 0 meter, en het is deze 0 die in de wiskunde uiteindelijk tot oneindigheden leidt.

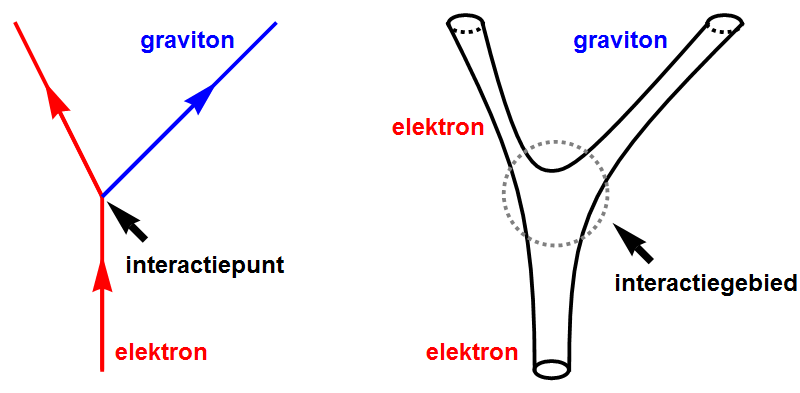
Afbeelding 3. Interacties tussen puntdeeltjes en tussen snaren.Interacties tussen puntdeeltjes en tussen snaren. Interacties tussen puntdeeltjes vinden plaats in een punt met grootte 0. Interacties tussen snaren vinden plaats in een groter gebied.

In de rechterhelft van afbeelding 3 zien we hoe zo’n zelfde interactie er in de snaartheorie uitziet. Zoals we hierboven uitgelegd hebben, zijn de verschillende ‘deeltjes’ in de snaartheorie te beschrijven als verschillende trillingen van hetzelfde type snaar. Het uitzenden van een graviton door een elektron kunnen we dus eenvoudigweg beschrijven als het opsplitsen van een enkele snaar. Het pad dat zo’n splitsende snaar in de ruimte aflegt is getekend in de rechterhelft van afbeelding 3. We zien dat de splitsing volkomen ‘glad’ is, en plaatsvindt in een gebied in plaats van in een punt. (De kleine lettertjes: we kunnen nog altijd wel een exact punt definiëren waar de snaar breekt, maar de snaren zelf nemen op dat moment een hoeveelheid ruimte in die een bepaalde grootte heeft. Daarnaast is het zo dat in de relativiteitstheorie het precieze punt waar de snaar breekt van waarnemer tot waarnemer verschilt, zodat de interactie ook in dat opzicht niet op één ‘ruimtetijdpunt’ plaatsvindt.) Dit gebied heeft een grootte die, hoewel het gaat om afstanden van de orde van 10^-35 meter, niet exact gelijkt aan nul is, en dat blijkt voldoende te zijn om de oneindigheden uit de berekeningen te doen verdwijnen. In de snaartheorie is dus niet eens renormalisatie nodig: de oneindigheden bestaan eenvoudigweg niet meer! Dit is de reden dat de snaartheorie in 1984 zo’n succesvolle kandidaat leek om de quantumzwaartekracht te beschrijven.

Naar boven

Open en gesloten snaren

Zoals gezegd: na de eerste snaarrevolutie bleek er uiteindelijk nog een tweede revolutie nodig om het punt te bereiken dat er algemene lessen, zoals het holografisch principe, uit de snaartheorie geleerd konden worden. In het komende artikel zullen we deze tweede snaarrevolutie beschrijven. Om die revolutie te begrijpen, moeten we onszelf de volgende vraag stellen. Zowel in de oorspronkelijke formule van Veneziano (met de interpretatie die Nambu, Susskind en Nielsen eraan gaven) als in de quantumzwaartekrachtstheorie van Scherk, Schwarz en Green, zijn de snaren kleine, gesloten lusjes. We hebben echter gezien dat dergelijke snaren kunnen opbreken in verschillende lusjes, zoals bij het uitzenden van een graviton door een elektron, dus de vraag ligt voor de hand of een snaar ook uit zichzelf kan openbreken en een ‘schoenveter’ met twee uiteinden kan vormen – zie afbeelding 4.

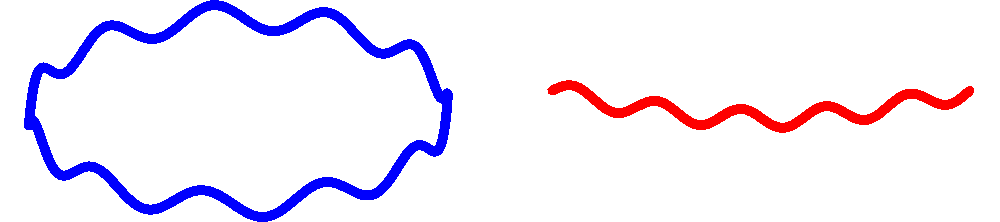
Afbeelding 4. Gesloten en open snaren.Om de zwaartekracht te beschrijven zijn alleen lusvormige, gesloten snaren (links) nodig. Hebben open snaren met twee eindpunten (rechts) ook een interpretatie die we kunnen gebruiken om de natuur om ons heen te beschrijven?

Dergelijke ‘schoenveters’ worden ‘open snaren’ genoemd, en het blijkt inderdaad mogelijk om theorieën op te stellen die zowel gesloten als open snaren beschrijven. (Een theorie van alleen open snaren blijkt niet te kunnen bestaan: zo’n snaar kan zichzelf altijd sluiten en een gesloten snaar vormen.)  De vraag is: hoe gedragen deze open snaren zich precies, en hebben ze een nut in het beschrijven van de wereld om ons heen? Het antwoord op deze vragen zullen we in de volgende twee artikelen zien.

In het vijfde artikel in dit dossier zullen we zien welke verschillende soorten snaartheorieën er kunnen bestaan.