Snaren en holografie (18): Snaren en de natuur

Dat neemt niet weg dat natuurkunde in haar grondvesten een experimentele wetenschap is. We kunnen elke theorie bedenken die we maar willen, maar uiteindelijk is de vraag of zo’n theorie, op zijn minst bij goede benadering, onze natuur beschrijft. Die vraag kan alleen door experimenten worden beantwoord. In dit voorlopig laatste artikel in dit dossier bekijken we de snaartheorie daarom door de ogen van de experimentator, en stellen we onszelf de vraag: beschrijft snaartheorie de natuur?

In dit artikel:

• Snaren als theorie van alles
• Snaren als inspiratiebron voor quantumzwaartekracht
• Snaartheorie als duaal model
• Snaren en de wiskunde
• Snaren en de natuur?

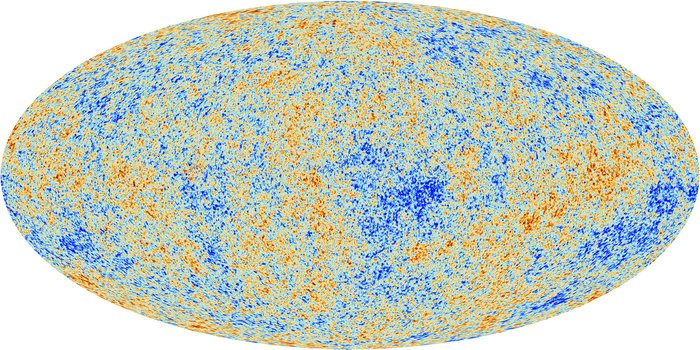
Afbeelding 1. De kosmische achtergrondstraling.Een kaart van de temperatuur van de kosmische achtergrondstraling, gemeten door de Planck-satelliet. Bevat deze kaart aanwijzingen over de rol van snaren in de natuur? Afbeelding: ESA.

Snaren als theorie van alles

Met name in de beginjaren van de snaartheorie werd de theorie vaak voorgesteld als een toekomstige “theorie van alles”: een theorie die niet alleen de quantummechanica en de zwaartekracht, maar ook de drie andere natuurkrachten beschrijft. Zoals we in dit dossier gezien hebben, is het inderdaad geen enkel probleem om krachten zoals de elektromagnetische kracht en de sterke en zwakke kernkracht met snaartheorie te beschrijven. Wanneer we van de in essentie tiendimensionale snaartheorie een vierdimensionaal model van de natuur maken, door zes dimensies op te rollen en eventueel hogerdimensionale D-branen toe te voegen, leveren de snaren die in de interne richtingen trillen of verbonden zijn aan de D-branen automatisch allerlei nieuwe deeltjes op. Deze deeltjes zorgen voor de uitwisseling van allerlei krachten zoals de elektromagnetische en de twee kernkrachten.

Het probleem is dat dit ‘oprollen’ op onnoemelijk veel manieren kan, en dat elk van die manieren leidt tot net iets andere vierdimensionale natuurwetten. De zoektocht naar een ‘compactificatie’ die exact onze natuur beschrijft, is nog altijd in volle gang. Het is maar zeer de vraag of zo’n manier uniek is en, belangrijker, of we die kunnen onderscheiden van de modellen die bijna onze natuur beschrijven. Totdat deze vragen beantwoord zijn lijkt het erg lastig om de snaartheorie als ’theorie van alles’ experimenteel te onderzoeken.

Afbeelding 2. Een magneet.Om een ’theorie van alles’ te zijn, moet de snaartheorie naast de zwaartekracht ook de overige natuurkrachten zoals het magnetisme beschrijven. Dit is op zichzelf geen probleem, maar de grote vraag is: welke compactificatie beschrijft exact die krachten, en hoe onderscheiden we zo’n model van modellen die er sterk op lijken? Foto: Eurico Zimbres.

Naar boven

Snaren als inspiratiebron voor quantumzwaartekracht

Wellicht moeten we dus voorlopig iets minder ambitieus zijn, en vragen of er meer algemene aspecten van de snaartheorie zijn die experimenteel onderzocht kunnen worden, zonder dat we een exacte compactificatie naar vier dimensies kennen. Een eerste overeenkomst die alle snaarmodellen hebben is natuurlijk dat de elementaire deeltjes in de theorie ééndimensionale snaren zijn in plaats van ‘klassieke’, nuldimensionale puntdeeltjes. Het eenvoudigste experiment om de snaartheorie te verifiëren (of falsificeren) zou dus zijn om een elementaire deeltje onder een microscoop te houden die sterk genoeg is om te kunnen zien of zo’n deeltje punt- of snaarvormig is.

Het probleem met deze aanpak is de lengte van de snaar. Die zou, om de quantumzwaartekracht te kunnen beschrijven, zo’n 10^-35 meter moeten zijn. De sterkste ‘microscoop’ die we op dit moment hebben, is de LHC-deeltjesversneller in Genève. Deze versneller is in staat om details te zien die zo’n 10^-20 meter groot zijn. We zijn dus nog maar liefst 20 ordes van grootte verwijderd van een experiment waarmee we snaren daadwerkelijk kunnen zien. Een versneller die volgens de huidige principes gebouwd zou worden zou om dit te kunnen ongeveer zo lang moeten zijn als de baan van Pluto. Helaas lijkt ook dit voorlopig dus geen haalbare manier om de snaartheorie te testen.

Dat neemt niet weg dat deze denkwijze – het zoeken naar algemene lessen uit de snaartheorie die experimenteel getest kunnen worden – wel eens vruchtbaar zou kunnen zijn. Zo was de oerknal zelf een enorme deeltjesversneller, en is het dus niet ondenkbaar dat er in het licht dat we nog altijd van de oerknal opvangen – de beroemde ‘achtergrondstraling’ – kenmerken terug te vinden zijn die al dan niet wijzen op het bestaan van snaardeeltjes. In zekere zin wordt deze denkwijze in omgekeerde richting al gebruikt: in de snaartheorie kunnen allerlei modellen opgesteld worden die de evolutie van het vroege heelal beschrijven, en veel van die modellen kunnen getest worden door te zien welke voorspellingen ze doen voor de statistische verdeling van temperatuur en polarisatie van het licht van de achtergrondstraling. Komt de voorspelling van zo’n model niet overeen met de waarnemingen, dan kan het model de prullenbak in. Individuele snaarmodellen kunnen zo dus gefalsificeerd worden. Het is niet uitgesloten dat op een dergelijke manier ook ofwel alle snaarmodellen gefalsificeerd kunnen worden, of dat juist aangetoond kan worden dat alle snaarmodellen bepaalde eigenschappen gemeen hebben die inderdaad in de achtergrondstraling voorkomen. Dergelijke onderzoeksideeën staan op dit moment volop in de belangstelling.

Afbeelding 3. Nogmaals de kosmische achtergrondstraling.De statistische verdeling van verschillende temperaturen in deze afbeelding zou een gevolg moeten zijn van de fysica die in het vroege heelal een rol speelde. Aangezien deze fysica plaatsvond bij enorm hoge temperaturen, energieën en dichtheden, zou het mogelijk moeten zijn om kenmerken van de quantumzwaartekracht uit deze verdeling af te lezen, en zo wellicht de snaartheorie te verifiëren of falsificeren. Afbeelding: ESA.

Naar boven

Snaartheorie als duaal model

Voortbordurend op de algemene lessen die we kunnen leren uit de snaartheorie, kunnen we ons ook afvragen of het idee van holografie tot meetbare resultaten leidt. We weten dat we snaarmodellen in een bepaald aantal dimensies vaak met een exacte wiskundige dualiteit ook kunnen beschrijven als modellen zonder zwaartekracht in een lager aantal dimensies. Uit dat holografische principe kunnen we allerlei algemene lessen leren.

Allereerst kunnen we er lessen uit leren over de manier waarop de quantummechanica en zwaartekracht in de snaartheorie worden samengebracht. Zo hebben we gezien dat met behulp van een dergelijke dualiteit de informatieparadox – de vraag of de straling uit zwarte gaten informatie bevat over de manier waarop ze gevormd zijn – opgelost kon worden. Verder redenerend in deze richting zouden we ons kunnen voorstellen dat snaartheorie veel meer zegt over de straling die zwarte gaten uitzenden, en over de processen die zich afspelen  op de rand van zwarte gaten. Het doen van waarnemingen of metingen aan zwarte gaten is natuurlijk niet eenvoudig. Ver in het heelal zijn zwarte gaten vaak lastig waar te nemen omdat ze zelf geen licht uitstralen en we dus alleen kunnen kijken naar wat zich in de buurt van het zwarte gat afspeelt. Op aarde microscopische zwarte gaten maken valt vanwege de enorme energieën die daarbij komen kijken ook niet mee. Ook hier zijn dus nog enkele hordes te nemen, maar ook in deze richting is het niet uitgesloten dat we binnenkort de eerste tests van de quantumzwaartekracht – al dan niet specifiek zoals die beschreven wordt door de snaartheorie – kunnen verwachten.

Afbeelding 4. Een artist impression van een zwart gat.Zwarte gaten direct waarnemen is erg moeilijk, maar we kunnen wel allerlei processen zien die zich in de buurt van zwarte gaten afspelen – hier bijvoorbeeld het opslokken van gas van een nabijgelegen ster. Door waarnemingen aan dergelijke processen kunnen hopelijk we meer leren over de aard van de quantumzwaartekracht. Afbeelding: NASA.

Ook als we het idee dat de natuur op microscopische schaal uit snaren bestaat, even laten varen, kan de holografische dualiteit verrassend genoeg nog altijd tot experimentele voorspellingen leiden. We kunnen de dualiteit immers ook in omgekeerde richting toepassen, en proberen om fysische systemen waarin de zwaartekracht géén rol speelt op duale wijze te beschrijven met een snaartheorie. De vraag is dan of zo’n snaarmodel voorspellingen doet die we niet gemakkelijk uit het oorspronkelijke model konden afleiden. In ons artikel over het quark-gluonplasma hebben we al voorbeelden van deze redenering gezien: snaartheorie doet meetbare voorspellingen over bijvoorbeeld de viscositeit (‘stroperigheid’) van dit medium dat het vroege heelal vulde. Dit is momenteel de meest directe route van snaartheorie naar experiment, al is het natuurlijk niet de snaarhypothese zelf die getest wordt. De snaartheorie wordt in deze opzet gebruikt als wiskundige beschrijving van een ander, al bestaand model, en dergelijke experimenten moeten dus meer gezien worden als (a) tests om te zien of het idee van dualiteiten juist is, en (b) een manier om te onderzoeken of een andere wiskundige beschrijving ook makkelijker experimentele voorspellingen kan doen dan de oorspronkelijke beschrijving.

Naar boven

Snaren en de wiskunde

Als we de term ‘experiment’ heel ruim nemen, blijkt de snaartheorie op nog een heel ander gebied experimentele voorspellingen te doen, namelijk in de wiskunde. Wiskunde is natuurlijk geen experimentele wetenschap, maar er zijn wel allerlei gebieden in de wiskunde waar enorm veel voorbeelden van een bepaalde structuur bestudeerd kunnen worden. Zo worden in de getaltheorie bijvoorbeeld priemgetallen bestudeerd: gehele getallen die alleen door 1 en door zichzelf te delen zijn. Er is een oneindig lange lijst voorbeelden: 2, 3, 5, 7, 11, 13, … Wiskundigen bewijzen natuurlijk het liefst algemene zaken, maar soms is het lastig om zo’n bewijs te vinden, en loont het de moeite om in plaats daarvan individuele voorbeelden te bestuderen. Een voorbeeld: het is een onbewezen vermoeden dat er oneindig veel paren van priemgetallen zijn die twee van elkaar af liggen, zoals 3 en 5, of 11 en 13. ‘Experimenteel’ is echter wel vastgesteld dat tot enorm grote waarden zulke tweelingparen voorkomen.

Verrassend genoeg blijkt ook voor de ‘experimentele wiskunde’ de snaartheorie een belangrijke rol te spelen. Zo zijn er bijvoorbeeld allerlei onbeantwoorde vragen van de vorm ‘als ik een bepaalde hogerdimensionale figuur heb, op hoeveel verschillende manieren kan ik dan een cirkel op die figuur tekenen’? Het blijkt dat dergelijke vragen – en hun antwoorden! – ook in de snaartheorie de kop op steken. Een dergelijke hogerdimensionale figuur kan namelijk gebruikt worden als compactificatiemodel om de snaartheorie terug te brengen van tien naar vier (of, aangezien we het toch niet over onze eigen natuur hebben, een willekeurig ander aantal) dimensies, en het aantal manieren om cirkels of andere figuren te tekenen vertaalt zich vaak in fysische eigenschappen van de deeltjes van het vierdimensionale model.

Een beroemd voorbeeld van de kracht van de snaartheorie in dit opzicht is dat in de jaren ’90 de fysici Philip Candelas, Xenia de la Ossa, Paul Green en Linda Parkes een voorspelling deden voor het aantal manieren waarop een oneindig grote klasse van verschillende tweedimensionale figuren op een bepaalde zesdimensionale figuur getekend konden worden. Voordat Candelas en zijn medewerkers dit resultaat publiceerden, was het antwoord bij wiskundigen alleen bekend voor twee heel specifieke tweedimensionale figuren, en werd het antwoord in de andere gevallen gezien als een enorm moeilijk wiskundig probleem!

Afbeelding 5. De quintic.Een driedimensionale doorsnede van de zesdimensionale figuur die in de snaartheorie bekend staat als de ‘quintic’, naar de vijfdegraads-vergelijking die gebruikt wordt om deze figuur te beschrijven. Tot de jaren ’90 was door wiskundigen alleen uitgerekend op hoeveel manieren twee specifieke tweedimensionale vormen op deze figuur getekend konden worden. In 1991 veranderde dit, toen natuurkundigen in één klap de aantallen manieren voor een oneindig grote klasse van tweedimensionale vormen berekenden.

Naar boven

Snaren en de natuur?

Als we dergelijke wiskundige ‘experimenten’ buiten beschouwing laten, zullen we moeten toegeven dat de oogst aan experimentele verificatie voor de snaartheorie op dit moment, al bijna 50 jaar na het ontstaan ervan, nog altijd karig is. Dat staat in schril contrast tot de successen die de snaartheorie op theoretisch vlak gehad heeft. Snaartheorie is een van de weinige modellen die erin slaagt om de quantummechanica en de zwaartekracht aan elkaar te koppelen, en zo zaken als de informatieparadox en de verschillende microscopische toestanden van zwarte gaten te beschrijven.

Tegelijkertijd lijken we op allerlei gebieden op de drempel te staan van het daadwerkelijk doen van metingen die ons meer leren over de quantumzwaartekracht in het algemeen en de snaartheorie in het bijzonder. Zulke metingen zullen ons uitsluitsel moeten geven over de vraag wat de band is tussen snaartheorie en de natuur. Allerlei resultaten zijn mogelijk: aan het ene uiteinde van het spectrum zouden we kunnen vinden dat de natuur om ons heen daadwerkelijk bestaat uit minuscule snaartjes die trillen in onze vier plus nog zes opgerolde dimensies. Aan het andere uiteinde ligt het resultaat dat snaartheorie niets met onze natuur te maken heeft – al blijven in dat geval alle algemene lessen die de wiskunde van de snaartheorie ons leert over andere quantumzwaartekrachtsmodellen natuurlijk bestaan. Of wellicht ligt de waarheid ergens in het midden, en komen we met behulp van een idee als het holografisch principe uiteindelijk uit bij een andere beschrijving van de quantumzwaartekracht die beter bij toekomstige experimenten aansluit. In dat geval zal wellicht de uitspraak van de snaartheoreet Nathan Seiberg gelden: “Most string theorists are very arrogant. If there is something beyond string theory, we will call it string theory.”

Welke van deze mogelijkheden de juiste is, kan alleen de toekomst ons leren. De huidige ontwikkelingen lijken er in elk geval op te duiden dat het niet nog eens 50 jaar zal duren voordat we ook op experimenteel gebied meer weten over de quantumzwaartekracht. Het woord is, zoals het hoort in de natuurkunde, in de komende jaren weer aan de natuur.