Snaren en holografie (14): Verstrengelingsentropie

In dit artikel:

• Entropie
• Verstrengeling
• Entropie van superposities
• Verstrengelingsentropie

Afbeelding 1. Verstrengelingsentropie.We verdelen een natuurkundig systeem willekeurig in twee delen: A en B. De vraag die centraal staat in dit artikel: kunnen we aan A en B afzonderlijk een entropie toekennen? En hoe zit dat als A en B quantummechanisch verstrengeld zijn? Foto: Brown University.

Entropie

Over het begrip entropie is op deze site al eerder een uitgebreide serie verschenen. Wie alle details wil weten, verwijzen we dus naar die serie; voor dit artikel volstaat een eenvoudige uitleg.

Entropie speelt een rol zodra we een bepaald natuurkundig systeem op twee verschillende niveaus kunnen beschrijven: één niveau waarop we alle details weergeven, en één niveau waarop we alleen in bepaalde grootschalige gevolgen van die details geïnteresseerd zijn. Als we bijvoorbeeld een container met gas willen beschrijven, kunnen we dat in principe doen op een microscopisch niveau, waarbij we van elk gasmolecuul de exacte plaats en snelheid beschrijven. Aan de andere kant zullen we in het algemeen alleen geïnteresseerd zijn in enkele macroscopische eigenschappen van het gas, zoals de druk, de temperatuur en het volume. Die grootheden volgen natuurlijk uit de microscopische eigenschappen, maar het omgekeerde is beslist niet waar: als we druk, temperatuur en volume van het gas weten, kunnen we niet alle microscopische details van het gas berekenen.

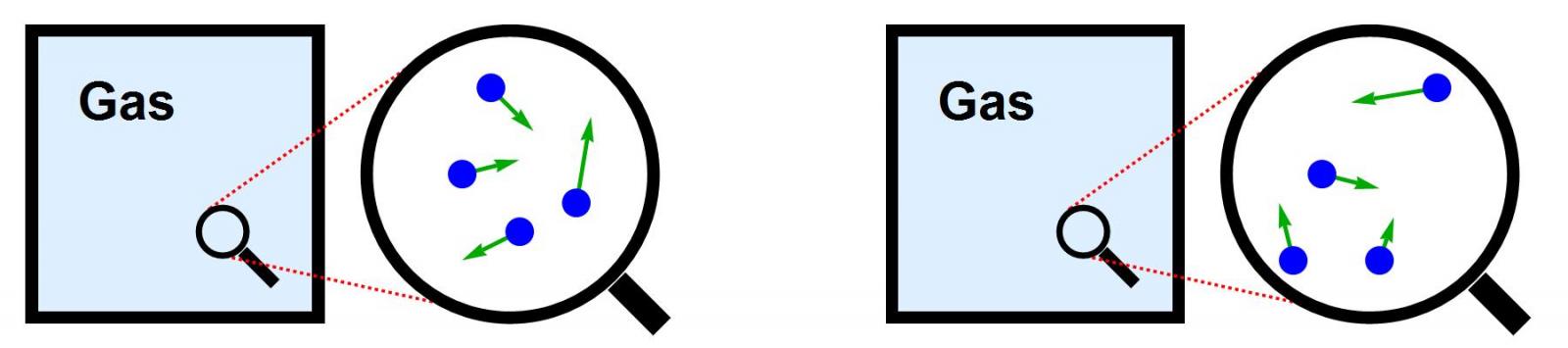
Afbeelding 2. Entropie.Eén macroscopische toestand van bijvoorbeeld een container met gas kan vaak op heel veel microscopische manieren opgebouwd worden. Entropie is een maat voor dit aantal manieren.

Kortom: als we van micro-schaal naar macro-schaal gaan, gooien we heel veel (irrelevante) informatie weg. Eén macroscopische toestand (een gas met een gegeven druk, volume en temperatuur) kan op enorm veel verschillende microscopische manieren worden gerealiseerd. Het begrip entropie is een maat voor op hoeveel manieren dit kan: de entropie S van een gegeven macroscopisch systeem is in een formule gedefinieerd als

S = k_B log(Ω)

In deze uitdrukking is Ω het totaal aantal microscopische toestanden, is k_B een bepaalde natuurconstante (de constante van Boltzmann) en staat ‘log’ voor de natuurlijke logaritme.

Het begrip entropie blijkt een heel belangrijke rol in de thermodynamica te spelen: het bepaalt bijvoorbeeld hoe een thermodynamisch systeem reageert op temperatuursveranderingen. Wie meer wil lezen over de rol van het begrip entropie in de thermodynamica verwijzen we naar dit artikel.

Ook wie zich zorgen maakt over de precieze definitie hierboven kunnen we met een link geruststellen. Een goede vraag is bijvoorbeeld: is het aantal microscopische toestanden dat bij een macroscopische toestand hoort niet oneindig groot? Het antwoord op deze vraag (en op de vervolgvraag: wat doen we in zo’n geval?) kunt u vinden in dit artikel. Voor het huidige artikel volstaat het beeld van entropie als een maat voor de hoeveelheid ‘weggegooide informatie’.

Naar boven

Verstrengeling

Ook het begrip verstrengeling is op deze website al eerder aan bod gekomen, dus ook daarvoor volstaan we met een eenvoudige beschrijving en verwijzen we de lezer naar de link voor verdere details.

Aan de basis van het begrip verstrengeling staat het quantummechanische begrip superpositie. In de quantummechanica is het niet altijd zo dat een systeem in één specifieke toestand is (een deeltje is bijvoorbeeld niet altijd op plaats 1 of plaats 2), maar kan het ook voorkomen dat het systeem in beide toestanden tegelijk is (het deeltje is deels op plaats 1, en deels op plaats 2). Pas als we meten waar zo’n deeltje zich bevindt, wordt één van de verschillende mogelijkheden gerealiseerd: pas dan wordt het ‘wazige’ deeltje dus een concreet deeltje dat zich op plaats 1 óf op plaats 2 bevindt. De wazige toestand vóór de meting heet een superpositie van toestanden.

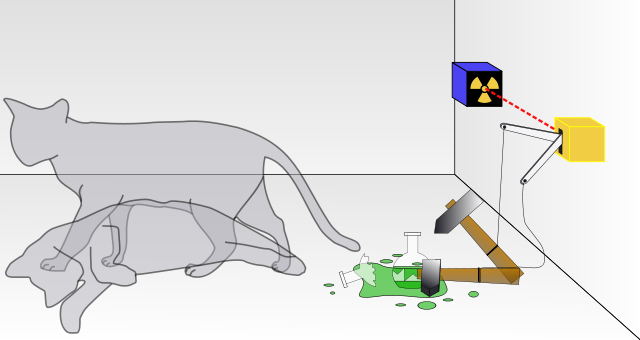
Afbeelding 3. De kat van Schrödinger.De kat van Schrödinger is misschien wel het beroemdste voorbeeld van een quantumsuperpositie. Door het leven van de kat te koppelen aan een radioactief atoom dat mogelijk wél of niét vervalt, komt de kat in een superpositie van ‘dood’ en ‘levend’ – een superpositie die pas wordt opgeheven zodra de kat wordt waargenomen. (De filosofische vraag is natuurlijk of de kat zichzelf kan waarnemen en of deze specifieke superpositie dus wel of niet kan bestaan; op die vraag gaan we in dit artikel verder niet in.) Afbeelding: Wikipedia-gebruiker Dhatfield.

Nog interessanter wordt het als we kijken naar systemen die opgebouwd zijn uit deelsystemen. Een heel simpel voorbeeld is een paar van deeltjes, waarbij de deelsystemen natuurlijk het ene deeltje en het andere deeltje zijn. Veel complexere voorbeelden zijn ook mogelijk: we kunnen de ruimte waarin een ingewikkeld natuurkundig experiment wordt uitgevoerd bijvoorbeeld opdelen in twee delen, A en B, en alles wat zich in A bevindt als één deelsysteem zien, en alles wat zich in B bevindt als het andere deelsysteem – zie afbeelding 1 bovenaan dit artikel.

Er zijn nu bijzondere quantummechanische superposities mogelijk, waarin een meting aan deelsysteem A ons iets vertelt over de toestand van deelsysteem B. We kunnen bijvoorbeeld een superpositie maken van de volgende twee specifieke toestanden:

1. Deeltje 1 bevindt zich op positie X en deelje 2 op positie Y, en
2. Deeltje 1 bevindt zich op positie W en deeltje 2 op positie Z.

Hierin staan W, X, Y en Z voor willekeurige maar verschillende posities. Als we van een systeem in deze superpositie nu meten waar deeltje 1 zich bevindt, vinden we het dus ofwel op positie X, ofwel op positie W. Op dat moment weten we echter onmiddellijk waar deeltje 2 zich bevindt: vinden we 1 op X, dan moet 2 zich op Y bevinden; vinden we 1 op W, dan moet 2 zich op Z bevinden. Vóór de meting aan deeltje 1 wisten we dus niet waar deeltje 2 zich bevond; door nu de positie van deeltje 1 te meten weten we ook onmiddellijk de positie van deeltje 2. We zeggen dat de posities van de deeltjes met elkaar verstrengeld zijn.

Ditzelfde kunnen we natuurlijk doen in het complexere voorbeeld met twee grote deelsystemen. Dan kunnen we bijvoorbeeld een superpositie maken van de toestanden

1. Deelsysteem A bevindt zich in toestand X en deelsysteem B in toestand Y, en
2. Deelsysteem A bevindt zich in toestand W en deelsysteem B in toestand Z.

Ook hier vertelt een meting aan A ons in welke toestand B zich bevindt, en omgekeerd.

Naar boven

Entropie van superposities

Beide bovenstaande onderwerpen, entropie en verstrengeling, zijn zoals gezegd al eerder op deze website langsgekomen. Wat nog niet eerder besproken is, is dat de twee ook gecombineerd kunnen worden. We kunnen onszelf namelijk afvragen: “Wat is de entropie van een systeem in superpositie?”

Bij het nadenken over deze vraag wordt het al snel duidelijk dat het gewone begrip entropie geen oplossing geeft. Om entropie ‘klassiek’ te berekenen tellen we zoals we hierboven gezien hebben het aantal microscopische toestanden dat hoort bij een gegeven macroscopische toestand. Die definitie werkt prima als het systeem wél of níet in een bepaalde microtoestand kan zijn: als het wél in die toestand kan zijn, tellen we de toestand mee; als het systeem níet in die toestand kan zijn, tellen we die niet mee. Maar hoe zit het als het systeem ook voor 50% in een bepaalde toestand kan zijn, zoals het geval is in een superpositie?

Afbeelding 4. Josiah Willard Gibbs (1839-1903).Gibbs staat bekend om zijn onderzoek in de thermodynamica; de Gibbs-entropie is één van zijn ontdekkingen.

Deze vraag is overigens niet uniek voor de quantummechanica. Ook in ‘klassieke’ systemen kan het voorkomen dat niet elke microscopische toestand dezelfde kans heeft om in een bepaalde macroscopische toestand voor te komen. Dat is bijvoorbeeld het geval als we ‘microscopisch’ definiëren op een schaal die wel kleiner is dan ‘macroscopisch, maar niet de allerkleinst mogelijke. Bijvoorbeeld: we delen een container met 1 m³ gas op in deelvolumes die elk 1 mm³ groot zijn.  De ‘microtoestand’ kunnen we dan beschrijven door druk en temperatuur van elk klein volume-element te geven; samen bouwen die de toestand van de hele container op. Niet elke mm³ zal op elk moment exact dezelfde druk hebben, maar de druk zal meestal vlak bij de gemiddelde druk liggen, en maar soms daar beduidend van afwijken. De microtoestand ‘alle deelvolumes hebben gemiddelde druk’ is dus veel waarschijnlijker dan de microtoestand ‘er is één deelvolume waarvan de druk iets afwijkt van de gemiddelde druk’. In dit voorbeeld heeft elke ‘microtoestand’ dus een bepaalde kans, en zijn niet al die kansen gelijk.

Het was de Amerikaanse natuurkundige J. Willard Gibbs die in de 19e eeuw ontdekte hoe de formule voor entropie uit te breiden valt naar het geval waarin alle microtoestanden een bijbehorende kans hebben. De formule die hij vond was

S = k_B Σ p_i log (1/p_i)

Hierin is p_i, een getal tussen 0 (0%) en 1 (100%), de kans dat een bepaalde microtoestand ‘i’ voorkomt, en houdt het sommatieteken Σ in dat we de bijdragen van elk van de microtoestanden bij elkaar optellen.

Wie handig is met formules kan zelf inzien dat deze definitie overgaat in de oude als elke microtoestand een gelijke kans heeft om voor te komen. Als er Ω verschillende toestanden zijn, is die kans immers gelijk aan 1/Ω, wat we kunnen invullen in de formule van Gibbs:

S = k_B Σ 1/Ω log (Ω)

Elke bijdrage in de som heeft dan dezelfde waarde, en het aantal van deze termen is precies gelijk aan het aantal mogelijke microtoestanden Ω. De totale entropie, na het optellen van alle bijdragen, is dus inderdaad

S = k_B log(Ω),

dus precies de uitdrukking die we aan het begin van dit artikel opschreven.

De uitdrukking voor de Gibbs-entropie is toe te passen op alle mogelijke systemen waarin de microtoestanden met een bepaalde kans voorkomen. Voor quantumsystemen staat het resultaat bekend als de Von Neumann-entropie. Ook in de informatica komt een soortgelijke uitdrukking voor; daar staat die bekend als de Shannon-entropie.

Naar boven

Verstrengelingsentropie

Het bovenstaande verhaal gold voor algemene quantumsuperposities, maar het wordt extra interessant als we kijken naar systemen die in een verstrengelde toestand zijn. Laten we daartoe ons systeem weer opdelen in twee deelsystemen, A en B. Zolang we aannemen dat we nog niets aan deelsysteem A gemeten hebben, kunnen we niets definitiefs zeggen over de toestand waarin B is. Wat wel kan, is een kansverdeling geven: we kunnen de kans berekenen dat we na meting deelsysteem B in toestand Y of in toestand Z zullen vinden. Van deze kansverdeling kunnen we nu de Von Neumann-entropie uitrekenen. De uitkomst van de berekening wordt de verstrengelingsentropie genoemd.

Waarom is deze verstrengelingsentropie zo’n interessante grootheid? Er zijn twee eigenschappen die daarvoor zorgen. Ten eerste hebben we hierboven de verstrengelingsentropie van deelsysteem B gedefinieerd, maar we hadden natuurlijk exact hetzelfde voor deelsysteem A kunnen doen. We hadden dan eerst de kansen op alle toestanden waarin A kan zijn uitgerekend, en vervolgens daarvan de Von Neumann-entropie uitgerekend. Het leuke is nu dat de uitkomst exact hetzelfde zou zijn! Dit is iets wat wiskundig bewezen kan worden (al gaat het helaas wat te ver om het bewijs hier uit te schrijven): als we een systeem verdelen in twee deelsystemen A en B, is de verstrengelingsentropie voor deelsysteem A gelijk aan de verstrengelingsentropie voor deelsysteem B. Het maakt dus niet uit welk deelsysteem we kiezen voor de berekening.

Afbeelding 5. Nogmaals verstrengelingsentropie.De verstrengelingsentropie voor deelsysteem A is gelijk aan die voor deelsysteem B. Bovendien is deze entropie vaak proportioneel met het de grootte van het oppervlak (hier weergegeven door de rode lijn, maar in werkelijkheid is zo’n oppervlak natuurlijk tweedimensionaal) dat de twee deelsystemen scheidt.

A en B hebben hun verstrengelingsentropie dus gemeenschappelijk. Is er iets anders wat A en B gemeenschappelijk hebben? Jazeker: het oppervlak dat A en B scheidt kunnen we zien als de ‘rand’ van zowel A als B.  (In het algemeen gaat het hier slechts een denkbeeldig ‘oppervlak’, natuurlijk – we kunnen ons systeem opdelen zoals we willen, dus er hoeft geen fysieke scheiding tussen A en B te zijn.) Er blijkt in veel gevallen een belangrijke relatie tussen deze twee zaken te zijn: in veel gevallen is de verstrengelingsentropie proportioneel met de grootte van het oppervlak dat A en B scheidt. Omgekeerd: als we dit weten, spreekt het voor zich dat die verstrengelingsentropie dus hetzelfde is voor A als voor B – ze hebben immers dezelfde rand.

Kortom: we hebben een vorm van entropie gevonden die bepaald wordt door het oppervlak van de rand van een bepaald gebied. Bij de fervente lezer van onze artikelen gaat er nu mogelijk een belletje rinkelen: ook zwarte gaten hebben immers de bijzondere eigenschap dat de entropie groeit met hun oppervlak. Is deze overeenkomst toevallig? Absoluut niet! Waarom niet? Dat zullen we zien in het volgende artikel.

Naar boven

In het vijftiende artikel in dit dossier zien we wat het begrip verstrengelingsentropie ons vertelt over de quantumzwaartekracht.