Snaren en holografie (8): Dualiteiten

In dit artikel:

• Dualiteiten
• Een voorbeeld: T-dualiteit
• Van heel groot naar heel klein
• M-theorie
• AdS/CFT

Afbeelding 1. Dualiteit.Een dualiteit is als een spiegelbeeld: op twee verschillende manieren wordt exact hetzelfde beschreven. Foto: Christoffer Engström.

Dualiteiten

Een natuurkundig model is een verzameling van formules die het gedrag van objecten in onze natuur zo goed mogelijk beschrijven. Allerlei eigenschappen van dergelijke objecten kunnen we in getalswaarden uitdrukken: posities, tijdstippen, temperaturen, energieën, enzovoort. We noemen dergelijke eigenschappen grootheden; de formules beschrijven de verbanden tussen deze grootheden en de manier waarop ze in de loop van de tijd veranderen. Om deze verbanden in een formule te kunnen opschrijven, geven we elke grootheid een ‘naam’ in de vorm van een enkele letter, die we een variabele noemen. Zo gebruiken we een E om een energie aan te geven, een m om een massa aan te geven, een c om de lichtsnelheid aan te geven, enzovoort. Het verband ‘de energie van een voorwerp in rust is gelijk aan zijn massa, tweemaal vermenigvuldigd met de lichtsnelheid’ valt daarmee een stuk korter te schrijven als ‘E=mc²‘.

Soms lijken natuurkundige formules sterk op elkaar, ondanks dat ze verbanden tussen totaal verschillende grootheden beschrijven. Laten we als voorbeeld daarvan eens kijken naar twee beroemde natuurwetten: de tweede wet van Newton, en de wet van Ohm.

De tweede wet van Newton is een wet uit de mechanica die beschrijft hoe een kracht (F) die we op een voorwerp uitoefenen, resulteert in een versnelling (a) van dat voorwerp. De versnelling blijkt af te hangen van de massa (m) van het voorwerp: om een zwaar voorwerp te versnellen is meer kracht nodig dan om een licht voorwerp te versnellen. Het precieze verband wordt weergegeven door de formule F=ma.

De wet van Ohm is een wet uit de elektriciteitsleer die beschrijft hoe groot de spanning (V) van een spanningsbron moet zijn om door een bepaald elektrisch circuit een stroom met een gegeven stroomsterkte (I)te laten lopen. Deze spanning hangt af van de weerstand (R) die de stroom in het circuit ondervindt: bij hogere weerstand is er meer spanning nodig om dezelfde stroomsterkte te genereren. In een formule is het precieze verband V=IR.

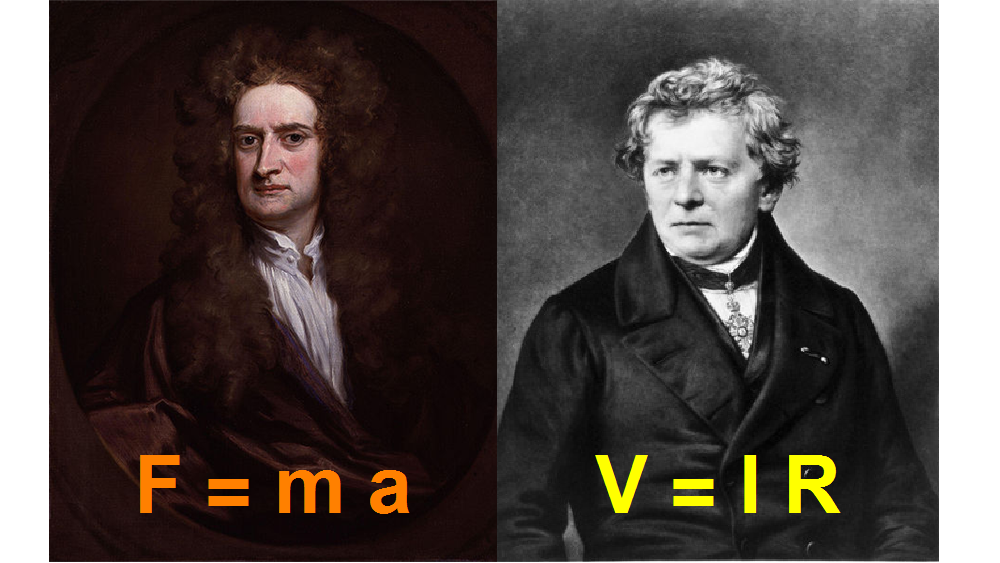
Afbeelding 2. Newton en Ohm.Isaac Newton, Georg Simon Ohm, en de naar hen vernoemde natuurwetten.

Wat misschien opvalt, is dat we het hier hebben over twee totaal verschillende natuurkundige systemen (een mechanisch systeem en een elektrisch systeem), maar dat de wiskunde uiteindelijk precies hetzelfde is. Om één grootheid uit te rekenen, moeten we twee andere grootheden met elkaar vermenigvuldigen. We hebben tweemaal precies dezelfde wiskundige formule gevonden: de letters die we in de formule gebruiken zijn verschillend, maar de berekeningen die we moeten doen zijn exact hetzelfde.

Hebben we daarmee een opvallende relatie tussen de elektriciteitsleer en de mechanica ontdekt? Nee, want die theorieën worden natuurlijk geen van beide beschreven door slechts één formule. In zowel de mechanica als de elektriciteitsleer komen allerlei andere formules voor, en het blijkt dat al die andere formules niet één op één op elkaar af te beelden zijn. (Zie hier voor een voorbeeld van een formule waarvoor dat bijvoorbeeld niet lukt.) De mechanica en de elektriciteitsleer zijn dus niet alleen natuurkundig, maar ook wiskundig gezien verschillende modellen.

Dit roept echter wel een interessante vraag op: zouden er ook natuurkundige modellen zijn waarvoor dergelijke relaties voor alle formules gelden? Met andere woorden: zijn er modellen waarin er een ‘vertaling’ is tussen de variabelen in het ene model en de variabelen in het andere model, op zo’n manier dat de wiskunde na deze vertaalslag in beide modellen exact hetzelfde blijkt te zijn? We zullen hieronder zien dat dergelijke modellen inderdaad bestaan! Als dit het geval is, worden dergelijke modellen duaal genoemd, en de ‘vertaling’ van het ene naar het andere model een dualiteit.

We kunnen nog een filosofische vervolgvraag stellen: als twee modellen duaal aan elkaar zijn, kunnen we dan überhaupt nog wel zeggen dat de twee modellen verschillende natuurkunde beschrijven? Als de modellen elk maar een deel van de natuur om ons heen beschrijven kunnen we dat nog wel volhouden, maar hoe zit het als de modellen de volledige natuur trachten te beschrijven? In dat geval kunnen we elk experiment en elke meting in het ene model omschrijven in een experiment of een meting in het andere model; een waarnemer die binnen het model zelf leeft (of, zo u wilt, een meetapparaat dat we uit de componenten van het model zelf kunnen bouwen) kan dus nooit het verschil tussen de twee modellen aantonen! Met andere woorden: we kunnen dan eigenlijk niet goed meer spreken over twee verschillende modellen; we zijn alleen op twee verschillende manieren op precies dezelfde natuurkunde uitgekomen. We zullen zien dat dit laatste precies geldt voor de vijf ‘verschillende’ snaarmodellen.

Naar boven

Een voorbeeld: T-dualiteit

In het vijfde artikel in dit dossier kwamen we de vijf verschillende snaarmodellen tegen. We bekijken nu twee van die theorieën, de type IIA- en de type IIB-theorie, iets beter. In het vijfde artikel hebben we gezien dat dit allebei theorieën zijn die gesloten, lusvormige snaren beschrijven. (We zagen later dat we in deze theorieën ook open snaren met eindpunten kunnen opnemen door D-branes toe te voegen, maar die laten we voor dit moment nog buiten beschouwing.) Het kleine verschil tussen deze theorieën ligt in de manieren waarop de snaren kunnen trillen – of, vertaald in termen van deeltjes: de twee theorieën beschrijven een iets ander ‘spectrum’ van elementaire deeltjes.

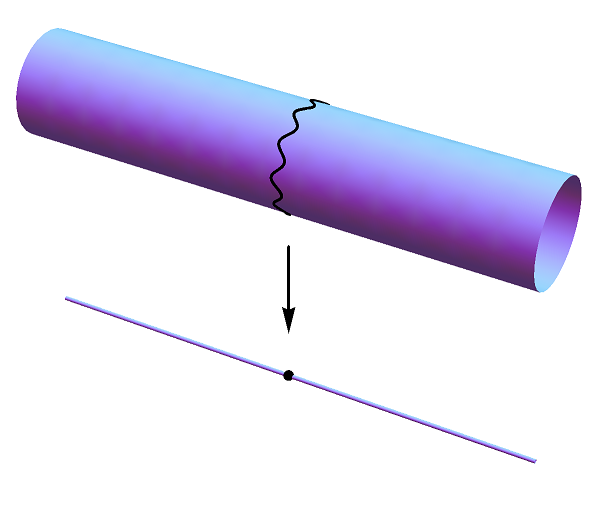
Afbeelding 3. Snaren en compacte dimensies.Een snaar kan om een compacte dimensie heen gewikkeld zijn, en als golf in de compacte richting bewegen. Beide eigenschappen nemen we op grote schaal waar als ‘interne’ bijdragen aan de energie van het snaardeeltje.

In het vorige artikel zagen we dat we het grote aantal dimensies van snaarmodellen kleiner kunnen maken door een aantal van die dimensies ‘op te rollen’, oftewel te compactificeren. Het eenvoudigste voorbeeld hiervan is het oprollen van één extra dimensie tot een cirkel. De theorie beschrijft dan dus snaren die op een soort cylinder bewegen – zie afbeelding 3, waarin we de opgerolde dimensie en één van de acht niet-opgerolde ruimtedimensies hebben getekend. (Het tekenen van alle negen de dimensies is natuurlijk erg lastig.)

Laten we nu aannemen dat we de IIA-theorie op deze manier compactificeren, en laten we ons afvragen wat dat betekent voor de deeltjes die we na het oprollen in de acht overblijvende ruimtedimensies (plus natuurlijk de altijd aanwezige tijddimensie) vinden. Eén eigenschap van deze deeltjes is de hoeveelheid energie die ze hebben. Die energie kan de vorm aannemen van bewegingsenergie, of potentiële energie (zoals de energie van een deeltje met massa in een zwaartekrachtsveld), maar die energie kan ook een oorsprong hebben in de opgerolde dimensie. Dat laatste kan zelfs op twee manieren.

De snaar kan ten eerste om de opgerolde dimensie heen gewikkeld zijn. Net zoals een elastiekje dat uitgerekt wordt een spanning opbouwt en daarmee extra energie krijgt, heeft ook een snaar meer energie naarmate die meer opgerekt is. Zo heeft een snaar die om de opgerolde dimensie gewikkeld is dus meer energie dan een snaar waarvoor dat niet het geval is. Bovendien kunnen we een snaar ook twee-, drie- of viermaal om de opgerolde dimensie heen wikkelen, waardoor de extra spannings-energie ook twee-, drie- of viermaal zo groot wordt.

Daarnaast kan de snaar in de compacte richting ronddraaien – een beweging die we natuurlijk zelf niet meer waarnemen als we deze richting heel klein maken, maar die de snaar wel extra energie geeft. De quantummechanica laat zien dat dit ronddraaien niet met willekeurige snelheden kan. In quantummechanische termen moeten we het ronddraaien van de snaar meer zien als een klein golfje dat rondom de cirkelrichting ‘stroomt’, en de golflengte van die golf moet natuurlijk op de cirkel passen. Met andere woorden: die golflengte moet precies even groot zijn als de cirkel, of half zo groot, of één derde van die grootte hebben, enzovoort. Als we de bij die beweging behorende energie uitrekenen, blijkt dat die voor het ‘enkele’ golfje een bepaalde waarde heeft; dat die energie voor het ’twee keer passende’ golfje twee keer zo groot is, voor het ‘drie keer passende’ golfje drie keer zo groot, enzovoort.

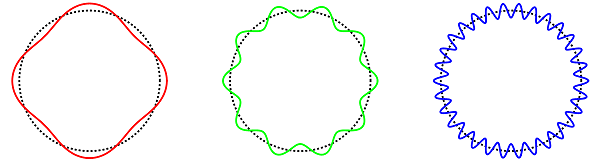
Afbeelding 4. Golven op een cirkel.De quantummechanica vertelt ons dat we elementaire deeltjes moeten beschrijven als golven. Als een golf zich op een cirkel bevindt, moet de golflengte precies een geheel aantal malen op die cirkel passen.

Kortom: er zijn twee getallen die bepalen hoeveel interne energie een op een cirkel gecompactificeerde snaar heeft. Het aantal windingen van de snaar – laten we dat n noemen – en het aantal golflengtes dat op de interne bewegingsrichting past – laten we dat m noemen. De interne energie is dus opgebouwd uit deze twee componenten. In een formule:

E = n E_w + m E_g

In deze formule is E_w de energie van een snaar die alleen één keer om de cirkel gewonden is, en E_g de energie van een snaar die als een precies één keer passende golf in de cirkelrichting beweegt.

Tot nu toe hebben we de IIA-theorie besproken, maar met de IIB-theorie kunnen we natuurlijk precies hetzelfde doen. Omdat deze theorie zoveel lijkt op de IIA-theorie zullen we daar een soortgelijke formule vinden voor de interne energie van de snaar. Het enige verschil tussen de twee theorieën blijkt te zijn dat de precieze getalswaarden die we vinden voor E_w en E_g in de twee theorieën verschillend zijn. Maar nu komt het opvallende: bij nadere bestudering blijkt dat de waarde die we voor E_g vinden in de IIA-theorie, exact gelijk is aan de waarde die we voor E_w vinden in de IIB-theorie, en omgekeerd! Met andere woorden, we vinden exact dezelfde formule in de twee theorieën, als we tenminste de getallen die deze waarden vermenigvuldigen, n en m, verwisselen. Een driemaal gewikkelde snaar die met twee golflengtes op de cirkel past in de IIA-theorie, heeft exact dezelfde interne energie als een tweemaal gewikkelde snaar die met drie golflengtes op de cirkel past in de IIB-theorie.

Deze situatie is vergelijkbaar met wat we eerder zagen voor de wetten van Newton en Ohm: met een eenvoudige ‘vertaling’ kunnen we de ene formule in de andere laten overgaan. Maar bij verder onderzoek blijkt dat de vertaling hier veel verder gaat, en dat we die kunnen toepassen op alle formules die de IIA- en IIB-theorie beschrijven. Met andere woorden: we hebben hier inderdaad twee duale theorieën gevonden: theorieën die op het eerste gezicht verschillend lijken, maar die uiteindelijk geheel beschreven worden door exact dezelfde wiskunde. In die zin zijn IIA en IIB, gecompactificeerd op een cirkel dus exact hetzelfde snaarmodel!

Naar boven

Van heel groot naar heel klein

We hebben in onze uitleg hierboven nog één aspect verwaarloosd: de energieën E_w en E_g hangen namelijk ook af van hoe groot (of beter: hoe klein) we de cirkel maken waarop we de snaartheorie oprollen. Voor E_w is dit eenvoudig in te zien: als we de cirkel relatief groot houden, moet de snaar flink uitrekken om om de cirkel heen te kunnen wikkelen. Daarmee is de spanning in de snaar, en de bijbehorende energie, dus groter dan als we een kleinere cirkel kiezen. Kortom: E_w wordt groter naarmate de straal van de cirkel groter wordt.

Afbeelding 5. Elastiekjes.Snaren zijn in meerdere opzichten te vergelijken met elastiekjes. Ook van snaren neemt de energie toe als ze opgerekt worden. Foto: Bill Ebbesen.

Het is lastiger om uit te rekenen hoe E_g verandert als we de straal van de cirkel aanpassen, maar daarvoor blijkt uiteindelijk precies het omgekeerde te gelden: E_g wordt juist kleiner naarmate de straal van de cirkel groter wordt. Bewegingen met een langere golflengte hebben dus minder energie – iets wat we ook kennen uit bijvoorbeeld de natuurkunde van straling. Infraroodstraling, met een lange golflengte, heeft beduidend minder energie dan ultraviolette straling, met een korte golflengte.

Hoe is dit gedrag te rijmen met het feit dat de windingsenergie in de IIA-theorie overeenkomt met de golfenergie in de IIB-theorie en omgekeerd? Wie hier goed over nadenkt vindt misschien zelf het antwoord: kennelijk is de IIA-theorie, opgerold op een cirkel met een heel grote straal, duaal aan de IIB-theorie, opgerold op een cirkel met een heel kleine straal, en omgekeerd. In IIA met een grote straal is E_w groot en E_g klein; in IIB met een kleine straal is E_g groot en E_w klein. Nauwkeurig rekenwerk laat zien dat dit resultaat inderdaad klopt: we kunnen precies uitrekenen hoe groot de cirkel in de IIB-theorie moet zijn (laten we de straal daarvan R_B noemen) om de natuurkunde uit de IIA-theorie met een cirkel van straal R_A te reproduceren. Het antwoord wordt gegeven door de formule

R_B = C / R_A

waarin C staat voor een bepaalde, constante (en heel kleine) getalswaarde. Kortom: Hoe groter R_A wordt, hoe kleiner R_B wordt, en omgekeerd. Delen door een groot getal geeft immers een klein getal; delen door een klein getal geeft een groot getal.

Wanneer we de groottes van de twee cirkels op deze manier aan elkaar relateren, blijkt dat de IIA- en de IIB-theorieën inderdaad exact duaal aan elkaar zijn. Dit is een vrij algemene les: in dualiteiten is er vrijwel altijd een grootheid die in de ene theorie heel klein is als de overeenkomstige grootheid in de andere theorie heel groot is, en omgekeerd. Deze op het oog onschuldige opmerking zal later in ons verhaal nog een heel belangrijke rol blijken te spelen!

Naar boven

M-theorie

T-dualiteit werd al vroeg in de geschiedenis van de snaartheorie ontdekt, maar de formulering zoals we die hierboven gaven stamt uit de jaren ’90. De dualiteit bleek het topje van een ijsberg: in de tweede helft van de jaren ’90 werden, onder meer door werk van de bekende Amerikaanse snaartheoreet Edward Witten, nog veel meer dualiteiten tussen snaarmodellen ontdekt.

Afbeelding 6. Edward Witten.Edward Witten ontdekte diverse snaardualiteiten, en ontdekte dat al deze dualiteiten leiden tot het bestaan van een overkoepelende M-theorie. Foto: Cliff Moore.

Uiteindelijk ontstond uit al die dualiteiten een beeld waarin alle vijf de snaartheorieën duaal aan elkaar zijn. Met andere woorden: het ging eigenlijk helemaal niet om vijf verschillende snaarmodellen; het ging om vijf verschillende beschrijvingen van exact dezelfde theorie. Waar sommige parameters in de ene beschrijving heel groot zijn, zijn die juist in de andere beschrijving heel klein. Daardoor is de ene beschrijving soms efficiënter dan de andere, maar uiteindelijk kunnen alle vijf de beschrijvingen in elkaar ‘vertaald’ worden.

Hiermee wordt misschien duidelijker waarom we het in dit dossier soms hebben gehad over ‘de snaartheorie’ en soms over ‘een snaartheorie’. Er zijn vijf verschillende snaartheorieën, maar uiteindelijk zijn alle vijf de theorieën verschillende incarnaties van één overkoepelende theorie. De vraag in de jaren ’90 was natuurlijk hoe deze theorie dan genoemd moest worden. Edward Witten kwam uiteindelijk met de naam M-theorie op de proppen, al is nooit helemaal duidelijk geworden waar de M in de naam dan precies voor staat. Volgens Witten zelf: “magic, mystery, or membrane, according to taste” – al zijn er ook boze tongen die beweren dat de M niets anders is dan een omgekeerde W, van Witten.

Wat de optie ‘membrane’ betreft: Witten kwam uiteindelijk ook nog met een zesde mogelijke beschrijving van deze zelfde theorie. Deze laatste beschrijving is er een in termen van trillende membranen (wat verklaart waarom die beschrijving niet als ‘snaartheorie’ was gevonden) – membranen die in maar liefst elf dimensies trillen. Deze beschrijving wordt vaak als de meest fundamentele gezien, aangezien alle andere snaartheorieën kunnen worden geconstrueerd door deze elfdimensionale theorie te compactificeren tot tien dimensies en vervolgens diverse dualiteiten toe te passen. Tegenwoordig wordt met de kreet ‘M-theorie’ dan ook meestal verwezen naar deze specifieke beschrijving van de theorie.

Naar boven

AdS/CFT

De ontdekking van de verschillende dualiteiten en van de overkoepelende M-theorie maakte de snaartheorie een stuk eleganter. Deze ontdekkingen waren dan ook van fundamenteel belang voor de populariteit van de snaartheorie in de jaren ’90 – een ontwikkeling die we al eerder bespraken en die de ’tweede snaarrevolutie’ genoemd werd. Ook de D-branes die we al eerder tegenkwamen speelden in deze ontwikkeling een belangrijke rol: die leverden vaak een goede test om te zien of voorgestelde dualiteiten daadwerkelijk klopten. Zo bleken de verschillende mogelijke D-branes in de type IIA-theorie door T-dualiteit exact vertaald te kunnen worden in de verschillende mogelijke D-branes in de type IIB-theorie.

In 1998 leidde de combinatie van alle ideeën die we tot nu toe besproken hebben – D-branes, compactificatie en dualiteiten – tot de ontdekking van een wel heel bijzondere dualiteit. Deze dualiteit, waarin ook het holografische principe voor het eerst heel duidelijk vorm kreeg, staat bekend als de AdS/CFT-correspondentie. Die correspondentie is het onderwerp van ons volgende artikel.

Een deel van de afbeeldingen uit dit artikel is eerder gepubliceerd in het boek ‘Snaartheorie‘ van de auteur.

In het negende artikel in dit dossier komen we de dualiteit tegen die aan de basis staat van het holografisch principe: de AdS/CFT-dualiteit.