Snaren en holografie (12): Het quark-gluonplasma

In dit artikel:

• Het quark-gluonplasma
• Schuif-viscositeit
• Holografie schiet te hulp
• Een lastiger vraagstuk

Afbeelding 1. Een plasmabal.Dit plasma, getoond in een demonstratie-experiment op het CERN, bestaat uit vrij bewegende elektrisch geladen deeltjes. In een quark-gluonplasma zijn het de ladingen voor de sterke kernkracht die vrij kunnen bewegen. Afbeelding: CERN.

Het quark-gluonplasma

In welke toestanden kan een materiaal zich bevinden? Wie heeft opgelet bij natuur- of scheikunde weet waarschijnlijk de bekendste antwoorden: een stof kan vast, vloeibaar of gasvormig zijn. Wat op de middelbare school soms niet wordt verteld, is dat er nog een vierde toestand (of fase) is waarin stoffen zich kunnen bevinden: die van een plasma.

Een plasma heeft veel weg van een gas of bij hoge dichtheid van een vloeistof: de deeltjes die het plasma vormen kunnen net als in gassen en vloeistoffen kriskras door elkaar bewegen. Het grote verschil met gassen en vloeistoffen is dat in een plasma ook de ladingen van de deeltjes kriskras door elkaar bewegen. In een gas zijn het altijd hele, ongeladen atomen of moleculen die bewegen. In een plasma zijn de bouwstenen opgebroken in hun geladen componenten (bijvoorbeeld in losse elektronen en atoomkernen), en bewegen ook die geladen componenten vrij door elkaar. Als de ladingen van de deeltjes vrij kunnen bewegen maar zich wel dicht genoeg bij elkaar bevinden om elkaar te kunnen beïnvloeden, spreken we van een plasma.

Op aarde komen we met name vaste stoffen, vloeistoffen en gassen tegen (vandaar de uitgebreide aanwezigheid van die fases in de middelbareschoolstof), maar diep in het heelal vinden we vooral plasma’s. Verreweg het grootste deel van de zichtbare materie in het heelal heeft de vorm van een plasma.

Misschien wel het beroemdste voorbeeld van een plasma kwam voor in de allervroegste fase van het heelal: vlak na de oerknal. Op dat moment was het heelal enorm heet en had het een gigantische dichtheid. Die twee eigenschappen zorgden ervoor dat in de eerste fractie van een seconde in het bestaan van het heelal geen enkel samengesteld deeltje kon bestaan. Alleen de allerkleinste elementaire deeltjes, zoals quarks, gluonen en elektronen, bestonden en krioelden willekeurig door elkaar. Niet alleen elektrische lading kon zich daarbij vrij rondbewegen; ook alle andere vormen van lading die we in de natuur kennen (en met name de lading die aan de sterke kernkracht onderhevig is) kon zich vrij verplaatsen. In die zin was dit plasma, dat het quark-gluonplasma wordt genoemd, dus een nog veel extremere vorm van een plasma dan de plasma’s die we in het huidige, afgekoelde heelal aantreffen, en waarin alleen elektrische lading vrij rondbeweegt.

Het quark-gluonplasma kwam in natuurlijke vorm met name in de eerste fractie van een seconde van het heelal voor, maar dat wil niet zeggen dat we het niet kunnen bestuderen. In deeltjesversnellers worden tegenwoordig namelijk met zulke hoge energieën elementaire deeltjes op elkaar geschoten, dat daarbij temperaturen en dichtheden ontstaan die vergelijkbaar zijn met die in het vroege heelal. Door de eindproducten van deze deeltjesbotsingen goed te bestuderen, kunnen we dus ook in aardse laboratoria van alles leren over het quark-gluonplasma.

Afbeelding 2. Meten aan het quark-gluonplasma.Een van de detectoren waarmee op het CERN in Genève het quark-gluonplasma bestudeerd wordt. Afbeelding: CERN.

Naar boven

Schuif-viscositeit

Een belangrijke eigenschap van het quark-gluonplasma is zijn zogeheten schuif-viscositeit – ook wel ‘dynamische viscositeit’ genoemd, en in het Engels ‘shear viscosity’. Het begrip viscositeit zegt iets over hoe materialen – met name vloeistoffen en plasma’s – reageren op bewegingen binnen het materiaal. Een ‘stroperig’ materiaal heeft een hoge viscositeit; een ‘waterig’ materiaal een lage viscositeit.

Iets preciezer kunnen we de schuif-viscositeit van een vloeistof of plasma als volgt definiëren. Neem twee grote vlakke platen, zet die op een kleine afstand y van elkaar, en zorg dat de ruimte tussen de platen gevuld is met de vloeistof of het plasma. Als we nu één van de twee platen in een parallelle richting bewegen (dus op zo’n manier dat de afstand tussen de platen niet verandert), dan zal dat een bepaalde hoeveelheid kracht kosten omdat de vloeistof of het plasma het schuiven ’tegenwerkt’. Hoe groot deze kracht is, hangt af van de ‘stroperigheid’: met water zal dit experiment veel minder kracht kosten dan met stroop of vloeibaar teer. In een formule blijkt de kracht die nodig is altijd bij goede benadering aan de volgende wet te voldoen:

F = η·A·v/y

Hierin is y zoals gezegd de afstand tussen de platen, A het oppervlak van de platen, v de snelheid waarmee we een van de platen bewegen, en F de kracht die nodig is. De variabele η, tenslotte, heeft een constante waarde die van materiaal tot materiaal verschilt. Deze constante wordt de schuif-viscositeit genoemd. Uit de formule blijkt duidelijk dat een grote waarde voor deze constante betekent dat er ook veel kracht gezet zal moeten worden om de platen te bewegen.

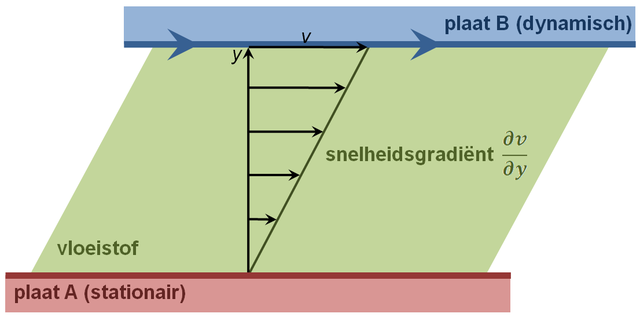
Afbeelding 3. Schuif-viscositeit.De onderste plaat (rood) staat stil; de bovenste (blauw) beweegt met een snelheid v. De vloeistof (groen) heeft een weerstand tegen deze beweging die zich manifesteert als een kracht die het schuiven van de bovenste plaat tegenwerkt. Afbeelding: Wikipedia-gebruiker Dr.T.

Naar boven

Holografie schiet te hulp

Het ligt natuurlijk voor de hand om de twee onderwerpen uit de bovenstaande hoofdstukjes te combineren, en te vragen: hoe groot is de schuif-viscositeit van een quark-gluonplasma? Deze vraag is uitermate interessant, aangezien ons hele heelal is ontstaan uit zo’n plasma . Hoe meer we over zo’n plasma weten, hoe beter we dus de dynamica van het ontstaan van het heelal kunnen begrijpen!

Helaas bleek noch het uitrekenen van de schuif-viscositeit, noch het meten ervan, een eenvoudige opgave. Wat het uitrekenen betreft: rekenen aan interacties van quarks is erg lastig aangezien de onderlinge krachten tussen deze deeltjes enorm groot zijn, en bovendien alleen maar groter worden naarmate de quarks zich verder van elkaar af bevinden. (Dit laatste is de reden dat we in onze dagelijkse natuur quarks altijd tegenkomen in neutraal geladen ‘kluitjes’ zoals protonen of neutronen.) Een exacte berekening van de schuif-viscositeit van een quark-gluonplasma kon daardoor niet gedaan worden. Het beste wat men tot grofweg het jaar 2000 kon doen, was het maken van benaderingen aan de hand van numerieke simulaties. Daaruit viel al wel iets bijzonders op te merken: de schuif-viscositeit van het quark-gluonplasma was onverwacht klein – veel kleiner dan men uit de meeste theoretische redeneringen zou verwachten.

In 2004 kwam er hulp uit voor kosmologen en experimentatoren onverwachte hoek: de snaartheorie. Uit het holografisch principe was immers gebleken dat het mogelijk was om vragen over quantumsystemen te vertalen in vragen over zwaartekrachtssystemen, en omgekeerd. Tot dan toe was die vertaalslag met name gebruikt om vragen te beantwoorden over zwaartekrachtssystemen – bijvoorbeeld over zwarte gaten. Nu bleek het echter mogelijk om precies het omgekeerde te doen: de berekening van de schuif-viscositeit van een quark-gluonplasma kon vertaald worden in een berekening in de zwaartekrachtsbeschrijving van een zwart gat. In die beschrijving bleek de berekening eenvoudiger te worden, en de snaartheoreten die de berekening voor het eerst deden (Pavel Kovtun, Dam Thanh Son en Andrei Starinets) vonden een minimale waarde voor de schuif-viscositeit die goed in de buurt kwam van de waarden die uit numerieke simulaties kwamen.

Zoals gezegd vonden Kovtun, Son en Starinets niet alleen een waarde voor de schuif-viscositeit van het quark-gluonplasma, maar toonden ze ook aan dat deze waarde de kleinst mogelijke waarde was die überhaupt in een heel brede klasse van modellen kon voorkomen. Daarmee deden ze dus nog een extra voorspelling: het zou in de natuur heel lastig moeten zijn om plasma’s of vloeistoffen te maken met een nog lagere schuif-viscositeit dan het quark-gluonplasma. Of dat ook onmogelijk is, is nog maar de vraag: het zou natuurlijk zo kunnen zijn dat er plasma’s of vloeistoffen bestaan die niet op een holografische manier met een dergelijke duale theorie te beschrijven zijn, en dat die materialen een nog lagere schuif-viscositeit kunnen hebben. Op dit moment is er echter geen enkel natuurlijk materiaal bekend dat deze eigenschap heeft.

Niet lang nadat Kovtun, Son en Starinets hun berekeningen hadden gedaan, in 2008, werd met de Relativistic Heavy Ion Collider (RHIC), een deeltjesversneller in Brookhaven op Long Island in Amerika, ook experimenteel de schuif-viscositeit van het quark-gluonplasma nauwkeurig bepaald. De gevonden waarde kwam goed overeen met de waarde die Kovtun, Son en Starinets berekend hadden!

Afbeelding 4. RHIC.Een deel van de RHIC-deeltjesversneller. Afbeelding: RHIC.

Het zou te ver gaan om te zeggen dat holografie daarmee een heilige graal voor de studie van het quark-gluonplasma is gebleken. Ook numerieke berekeningen waren immers al rond dezelfde waarde uitgekomen; een geheel nieuwe voorspelling had de holografie dus niet gedaan. Bovendien is de quantumveldentheorie die met het holografische systeem van Juan Maldacena bestudeerd kon worden niet exact de theorie die het fysische quark-gluonplasma beschrijft: zoals we in dit artikel zagen heeft die theorie allerlei symmetrieën (conforme symmetrie en supersymmetrie) die het echte quark-gluonplasma niet heeft. Toch is het zeer indrukwekkend dat uit een dergelijk ’toy model’ met een zuiver theoretische (dus niet numerieke) redenering een dusdanig goede waarde voor een experimenteel te meten grootheid bepaald kon worden!

Naar boven

Een lastiger vraagstuk

De vervolgvraag was natuurlijk: kan er met behulp van holografie nog meer over het quark-gluonplasma gezegd worden? Kunnen we andere lessen leren die zonder deze ‘vertaalslag’ lastig te leren zouden zijn? Een goede richting om in te zoeken is de zogeheten jet quenching in het quark-gluonplasma – een term waarvoor op dit moment nog geen gangbare Nederlandse vertaling bestaat.

Wanneer elementaire deeltjes met hoge energie op elkaar botsen, vliegen de ‘brokstukken’ alle kanten op. Wanneer deze brokstukken quarks zijn, gebeurt er iets bijzonders. Quarks kunnen vanwege de steeds groter wordende kracht als we ze ver uit elkaar halen namelijk, zoals we hierboven al noemden, niet goed op zichzelf bestaan. Als een individueel quark ver van zijn ‘partners’ weg vliegt, ontstaat daarbij zoveel energie dat uit het vacuüm een nieuw, neutraal quark-antiquarkpaar wordt gevormd. Eén van deze quarks vliegt mee met het zich verwijderende quark, zodat dat weer een neutraal deeltje kan vormen; het andere blijft achter. Als de energie van de botsing maar hoog genoeg is, blijft dit proces zich herhalen. Uiteindelijk heeft dat tot gevolg dat er uit een botsing een hele ‘straal’ (Engels: jet) van quarks voortkomt. Een eenvoudige botsing heeft twee van deze jets (één jet alleen kan nooit voorkomen vanwege een natuurwet die zegt dat de totale impuls bij een botsing behouden moet zijn), maar bij meer complexe botsingen kunnen ook drie, vier of nog meer jets voorkomen.

Afbeelding 5. Twee jets.Een opname van een botsing in de CMS-detector op het CERN in Genève. De rode en blauwe blokjes geven aan waar de ‘brokstukken’ van de botsing gemeten zijn. Twee jets zijn duidelijk zichtbaar. Afbeelding: CERN.

Wanneer bij de botsing de energie bovendien zo hoog is dat plaatselijk een quark-gluonplasma ontstaat, worden deze jets bij hun interactie met het plasma vertraagd. Deze vertraging wordt ‘quenching’ genoemd; quenching is een Engels woord voor ‘verminderen’. (‘Dorst lessen’ is in het Engels bijvoorbeeld ’to quench one’s thirst’.) Hoe groot deze vertraging precies is, wordt bepaald door een parameter die de ‘jet quenching parameter’ heet. Ook hier is weer sprake van een parameter die experimenteel en numeriek bepaald kan worden, maar waarvoor geen goede theoretische afleiding bestaat. De vraag is dus: kan deze parameter vanuit een holografische redenering berekend worden?

Aan deze vraag is de afgelopen jaren door een groot aantal snaartheoreten gewerkt. Een definitieve conclusie is er nog niet: het blijkt erg lastig te zijn om een holografisch duaal model te vinden dat exact de juiste eigenschappen van het quark-gluonplasma beschrijft. Veel modellen geven een kwalitatief juiste of deels juiste beschrijving, maar een exacte en algemeen geaccepteerde waarde van de parameter zoals die voor de schuif-viscositeit wel gevonden is, is nog altijd niet afgeleid. Het zal interessant zijn om te zien of dit in de nabije toekomst wel gaat lukken, en of holografie daarmee (of op heel andere, onverwachte wijze) input blijft leveren voor de studie van het quark-gluonplasma in het vroege heelal.

Naar boven

In het dertiende artikel in dit dossier gaan we op zoek naar het holografisch principe aan de waarneembare sterrenhemel.