Snaren en holografie (6): D-branen

In dit artikel:

• D-branen
• Snaartheorieën revisited
• p-branen
• De tweede snaarrevolutie
• Dualiteiten

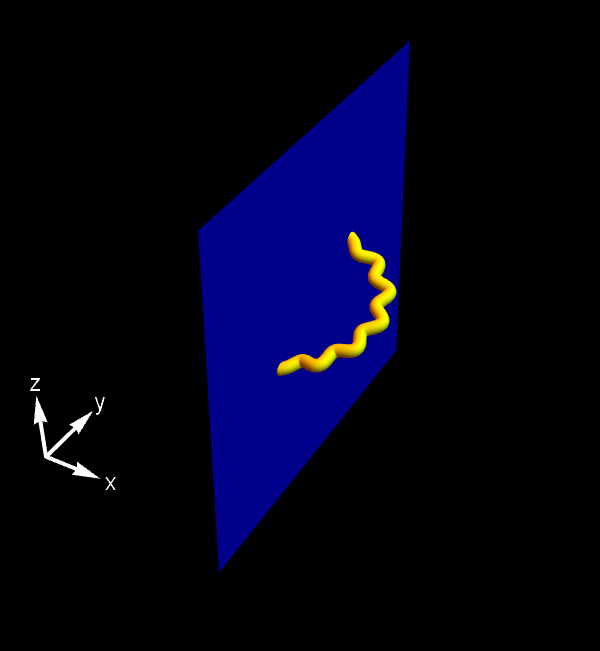
Afbeelding 1. Een D-braan.De open snaar (geel) kan in 3 dimensies trillen, maar zijn eindpunten zijn beperkt tot bewegingen langs de 2-dimensionale D-braan (blauw).

D-branen

De snaartheorie waarin open snaren op de meest natuurlijke wijze voorkomen, is de type I-snaartheorie. (Zie het vorige artikel voor een overzicht van de vijf typen snaartheorieën: type I, type IIA en IIB, en de twee heterotische theorieën.) Eén manier om deze theorie op te bouwen is om te beginnen met het idee van open snaren, en vervolgens alle wiskundige consistentie-eisen op te leggen bij het kiezen van de verdere eigenschappen van de theorie. Op die manier vinden we bijvoorbeeld vanzelf dat de theorie ook gesloten snaren moet bevatten en dat de theorie supersymmetrisch moet zijn – twee zaken die we ook in het vorige artikel in wat meer detail hebben uitgelegd. Na de nodige wiskunde blijken de consistentie-eisen zo strikt te zijn, dat deze opbouw tot één enkele theorie leidt: de type I-theorie.

Zonder het te merken, hebben we in die opbouw echter een belangrijke aanname gemaakt. De open snaren waar we mee begonnen zijn namelijk snaren die, zoals we van elementaire deeltjes kunnen verwachten, door de hele ruimte kunnen bewegen. Een belangrijke eigenschap van open snaren is echter dat ze twee eindpunten hebben. We kunnen onszelf daarom de volgende vraag stellen: “Kunnen deze eindpunten ook daadwerkelijk ergens op eindigen?” Met andere woorden: moeten de eindpunten van de open snaren ook vrij zijn om te gaan en te staan waar ze willen, of kunnen we die eindpunten ook zien als een soort ‘magneetjes’ die de snaren ergens aan vastplakken?

Het blijkt inderdaad mogelijk te zijn om de snaarmodellen zo uit te breiden dat er ook open snaren in voorkomen die op deze manier ergens aan vastgeplakt zijn – zie afbeelding 1 hierboven. Dat wil zeggen: we kunnen een lagerdimensionale ruimte binnen de gehele ruimte vastleggen, en eisen dat er in de theorie open snaren voorkomen waarvan de eindpunten alleen binnen deze lagerdimensionale ruimte mogen bewegen. In afbeelding 1 zien we bijvoorbeeld een driedimensionale ruimte (met coördinaten x, y en z) waarbinnen zich een tweedimensionaal vlak bevindt dat zich in de alleen in de y– en z-richtingen uitstrekt. In de afbeelding zien we een open snaar die in alle drie de ruimtedimensies kan trillen, maar waarvan we de eindpunten in hun bewegingsvrijheid beperkt hebben tot het tweedimensionale vlak.

Het verrassende is nu dat het mogelijk is om dergelijke theorieën op te stellen zonder dat de strikte wiskundige consistentie-eisen geschonden worden. Dat dit zo is werd in 1989 ontdekt door de snaartheoreten Jin Dai, Robert Leigh, Joseph Polchinski en (in een onafhankelijk artikel) Petr Hořava. Maar wat beschrijft een dergelijke theorie? Waarom zou het überhaupt nuttig zijn om een snaar te beschrijven die zo in zijn beweging beperkt is? De constructie lijkt nogal willekeurig als we die presenteren in termen van “beperken tot een tweedimensionaal vlak”. Maar wat als het tweedimensionale vlak zelf de beschrijving is van een natuurkundig object? Is het mogelijk dat in een snaartheorie ook ‘voorwerpen’ voorkomen die een ander aantal dimensies hebben dan de snaren, en die de open snaren als een soort ‘luizen in de pels’ met zich meedragen?

Dit laatste – zonder dan misschien de vergelijking met luizen – bleek inderdaad het geval te zijn. De deelruimtes waarop snaren konden eindigen bleken niet noodzakelijk star en recht te hoeven zijn, zoals het tweedimensionale vlak hierboven. Ze konden ook gekromd zijn, en zelf trillen of op andere manieren bewegen. Bovendien bleek dat de objecten zich in de theorie gedragen alsof ze allerlei natuurkundige eigenschappen hebben zoals massa’s en ladingen waarmee ze elkaar en andere objecten aantrekken. Kortom: de ‘voorwerpen’ waarop snaren kunnen eindigen bleken zelf een soort hogerdimensionale, dynamische ‘deeltjes’ te zijn. Deze objecten kregen de naam D-braan: ‘braan’ als generalisatie van ‘membraan’, en ‘D’ voor de naam ‘Dirichlet’ – een wiskundige die lang voor het ontstaan van de snaartheorie als een van de eersten de wiskunde onderzocht die beschrijft hoe open snaren precies op D-branen kunnen eindigen.

Naar boven

Snaartheorieën revisited

Betekent dit alles dat we nu in een willekeurige snaartheorie ook willekeurige D-branen als extra ‘deeltjes’ kunnen opnemen, en dat de theorie dan nog altijd vrij is van wiskundige problemen? Dat blijkt niet helemaal het geval: ook hier leggen wiskundige eisen weer allerlei beperkingen op aan de mogelijke D-branen die de theorie kan bevatten.

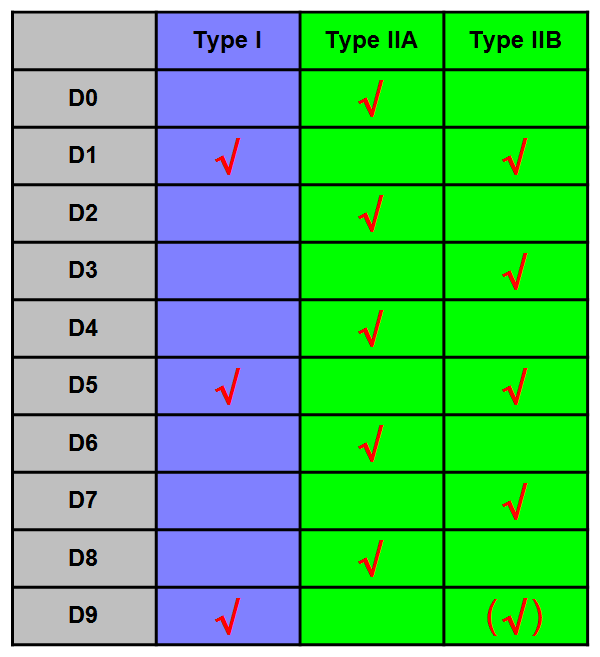
Afbeelding 2. Types D-branen.De verschillende types D-branen die de snaartheorieën van type I en type II kunnen bevatten.

De belangrijkste van die beperkingen is dat we geen D-branen van een willekeurig aantal dimensies kunnen maken. In het volgende artikel zullen we zien dat de vijf snaartheorieën die we tot nu toe hebben beschreven tiendimensionaal zijn: ze spelen zich dus niet alleen af in onze gebruikelijke vier dimensies (drie voor de ruimte, één voor de tijd), maar hebben nog zes extra richtingen waarin de snaren kunnen trillen. Hoe we ons die richtingen precies moeten voorstellen, en waarom we die in het dagelijks leven niet zien, bespreken we in het volgende artikel. Voor nu is van belang dat een D-braan dus niet alleen nul-, één- of tweedimensionaal hoeft te zijn, maar ook meer dimensies kan hebben – zolang dat aantal dimensies maar hooguit negen is. De tijd, de tiende dimensie, tellen we in het algemeen niet mee, omdat elke gewone D-braan door de tijd beweegt. Een puntdeeltje noemen we immers ook nuldimensionaal – niet ééndimensionaal omdat het ook een ’tijdrichting’ heeft.

De beperking op het aantal dimensies van een D-braan blijkt als volgt te zijn. (Zie ook de tabel hierboven.) In de type I-snaartheorie kunnen D-branen voorkomen die 1- of 5-dimensionaal zijn. Daarnaast kunnen open snaren zoals gezegd in de type I-theorie ook vrij door de ruimte bewegen – een eigenschap die we natuurlijk even goed (en wiskundig gezien zelfs beter) kunnen beschrijven door te zeggen dat de eindpunten van deze open snaren eindigen op een 9-dimensionale, ruimtevullende D-braan. Om de notatie wat te verkorten, zeggen we dat er in type I-theorieën D1-, D5- en D9-branen bestaan.

Hoe zit het met de andere vier snaartheorieën? Zoals we gezien hebben, zijn die theorieën opgebouwd als theorieën van gesloten snaren. Met behulp van D-branen blijkt het echter toch mogelijk te zijn om in twee van de theorieën – de type II-theorieën – open snaren op te nemen. Deze twee theorieën zijn in zekere zin complementair. In de IIA-theorie komen alleen D-branen voor met een even aantal dimensies: een nuldimensionale, puntvormige D-braan; een tweedimensionale ‘membraan’, en de hoger-dimensionale D4-, D6- en D8-branen. In de IIB-theorie komen juist de D-branen voor met een oneven aantal dimensies: een ééndimensionale ‘D-snaar’, een driedimensionale D3-braan, en de hogerdimensionale D5- en D7-branen. In zekere zin is het ook mogelijk om D9-branen in de theorie op te nemen, die dus alle dimensies vullen, maar als we dit op een consistente manier willen doen, blijken we uiteindelijk weer bij de Type I-theorie van open snaren uit te komen. In de heterotische snaartheorieën komen geen D-branen voor.

Het bestaan van D-branen beantwoordt direct een vraag die bij veel mensen opkomt wanneer ze voor het eerst over de snaartheorie horen: waarom is het zo’n goed idee om puntdeeltjes juist door ééndimensionale snaren te vervangen? Waarom maken we geen theorieën van twee-, drie- of zelfs hogerdimensionale objecten? Door het bestaan van D-branen is de snaartheorie in zekere zin veel ‘democratischer’ geworden: dergelijke hogerdimensionale objecten komen wel degelijk ook in de theorie voor. Sterker nog: voor zover we weten is de enige manier om een theorie van hogerdimensionale objecten consistent te maken, door ze op te nemen in een snaartheorie!

Samenvattend: dankzij de aanwezigheid van D-branen in de type I- en type II-theorieën, blijken er in de snaartheorie veel meer mogelijkheden te zijn om open snaren op te nemen dan op het eerste gezicht het geval was. In de komende artikelen zullen we zien dat juist deze D-branen en de daarop eindigende open snaren cruciaal zullen zijn in het begrijpen van het holografisch principe.

Naar boven

p-branen

Snaartheorie is, zoals we inmiddels weten, een theorie van de quantumzwaartekracht. We kunnen verwachten dat het in de theorie dus in elk geval mogelijk is om alles te doen wat in een ‘gewone’ zwaartekrachtstheorie ook mogelijk is. In het bijzonder betekent dat, dat in de theorie ook zwarte gaten moeten bestaan: opeenhopingen van materie die zo’n sterke zwaartekracht hebben dat zelfs het licht er niet aan kan ontsnappen.

Afbeelding 3. Een zwart gat.In ons heelal is het centrum van een zwart gat (de singulariteit) een nuldimensionale punt. In snaartheorieën kunnen echter ook zwarte gaten voorkomen die zich langs meerdere dimensies uitstrekken. Afbeelding: NASA.

Dat laatste bleek inderdaad het geval: de snaartheorie reproduceert de relativiteitstheorie van Einstein (en vult die theorie verder aan), en de vergelijkingen van de theorie hebben dus inderdaad oplossingen die zwarte gaten beschrijven. Doordat snaartheorie in meer dan drie ruimtedimensies geformuleerd is, blijkt er echter nog veel meer mogelijk. Naast bolvormige zwarte gaten waarvan het centrum (de singulariteit) een punt is, is het in de snaartheorie ook mogelijk om hogerdimensionale zwarte gaten te construeren waarvan het centrum een ééndimensionale lijn, een tweedimensionaal membraan, of een hogerdimensionale vorm is. Deze ‘zwarte objecten’ kregen al snel de naam p-branen, waarin de ‘p’ staat voor een getal van 0 t/m 9 dat de dimensie van de singulariteit in het object aangeeft. (Een 0-braan is dus een gewoon zwart gat, een 1-braan een ‘zwarte snaar’, enzovoort.)

We lijken nu te kampen te hebben met een ‘embarrasment of riches’. Snaartheorie bevat niet alleen ééndimensionale snaren, maar ook hogerdimensionale D-branen en hogerdimensionale zwarte p-branen. In de chaos van deze deeltjesdierentuin kwam echter in 1995 beduidend meer orde.

Naar boven

De tweede snaarrevolutie

In 1995 verscheen een artikel van de Amerikaanse snaartheoreet Joe Polchinski – één van de ontdekkers van de D-branen in 1989 – met de titel ‘Dirichlet-branes and Ramond-Ramond charges’. In het artikel liet Polchinski zien dat D-branen exact dezelfde lading en massa hebben als de overeenkomstige zwarte p-branen. Met andere woorden: D-branen en p-branen lijken sprekend op elkaar! Polchinski suggereerde dat beide objecten in feite twee verschijningsvormen van precies hetzelfde object waren: een beschrijving als D-braan is de manier waarop open snaren deze objecten ‘zien’; een beschrijving als zwarte p-braan de manier waarop de zwaartekracht (die zoals we gezegd hebben wordt overgebracht door gesloten snaren) de objecten ziet. In het bijzonder is het zo dat ook op het aantal dimensies van zwarte p-branen allerlei restricties blijken te zijn; die restricties komen exact overeen met de restricties op D-branen.

Afbeelding 4. Joseph Polchinski.Polchinski ontdekte in 1989 samen met zijn collega’s D-branes, en bewees in 1995 dat D-branes en zwarte p-branes exact dezelfde objecten waren.

Verder onderzoek bevestigde de ideeën van Polchinski: D-branen zijn zwarte p-branen. Deze op het oog eenvoudige ontdekking leidde tot een tweede revolutie in de snaartheorie. (De eerste revolutie had plaatsgevonden toen John Schwarz en Michael Green aantoonden dat snaartheorieën anomalievrij en dus wiskundig consistent konden zijn.) Het grote belang van deze revolutie was niet alleen dat het aantal verschillende objecten drastisch afnam; veel belangrijker was het dat we één en hetzelfde object (een D-braan) nu op twee verschillende manieren konden beschrijven: zowel als een object waarop open snaren kunnen eindigen, als als een hogerdimensionaal zwart gat. Al snel zou blijken dat juist deze dubbele beschrijving – en allerlei soortgelijke dubbele beschrijvingen – de studie van de snaartheorie enorm vooruit zouden helpen.

Naar boven

Dualiteiten

In de komende artikelen zullen we zien dat het op twee manieren kunnen beschrijven van één en hetzelfde object een voorbeeld is van wat we een dualiteit noemen. Dualiteiten zijn in de snaartheorie alomtegenwoordig: uiteindelijk blijken zelfs de vijf verschillende snaartheorieën aan de hand van dergelijke dualiteiten vijf verschillende beschrijvingen te zijn van één en dezelfde theorie! Voor we dit verder kunnen uitleggen, zullen we echter iets meer moeten weten over de mysterieuze tien dimensies van de snaartheorie – en over de vraag hoe we met al die dimensies uiteindelijk toch onze vierdimensionale natuur kunnen beschrijven. Dat laatste is het onderwerp van het volgende artikel in deze serie.

Naar boven

In het zevende artikel in dit dossier zien we dat snaartheorie een tiendimensionaal model is, en bespreken we hoe we daarmee toch onze vierdimensionale natuur kunnen beschrijven.