Snaren en holografie (13): Kerr/CFT

In dit artikel:

• AdS/CFT in de natuur
• Symmetrieën
• Kerr-zwarte gaten
• Kerr/CFT aan de sterrenhemel

Afbeelding 1. De sterrenhemel rond de dubbelster GRS1915+105.Kunnen we rond deze dubbelster het holografisch principe in de praktijk in actie zien? Foto: Chandra X-Ray Observatory.

AdS/CFT in de natuur

Hoe zien we het verschil tussen een snaarmodel en een model van puntdeeltjes in een experiment? We zullen in een later artikel nog uitgebreid op deze vraag terugkomen, maar het meest naïeve antwoord is dat we daarvoor zullen moeten “inzoomen” tot grofweg de grootte van de gemiddelde snaar. Op veel grotere schaal zijn snaren immers zo minuscuul dat we de verschillen met puntdeeltjes nauwelijks zullen kunnen waarnemen. Nu wil het geval dat de snaren in de snaartheorie van de quantumzwaartekracht zo’n 10^-35 meter groot zijn – een lengte die enorm veel kleiner is dan de allerkleinste afstand (zo’n 10^-19 meter) waarop we in de beste deeltjesversnellers metingen kunnen doen. Het moge dus duidelijk zijn dat het direct meten van snaar-effecten in experimenten een enorm lastige opgave is!

Nu speelt de quantumzwaartekracht zich wel grotendeels, maar niet uitsluitend af op die minuscuul kleine schaal. We hebben in diverse artikelen in dit dossier en in het dossier over zwarte gaten bijvoorbeeld kunnen lezen dat ook voor het begrijpen van allerlei effecten die zich op de rand (of horizon) van een zwart gat afspelen, een theorie van de quantumzwaartekracht nodig is. Zo’n horizon is voor een gemiddeld zwart gat dat uit een ster is ontstaan, al snel enkele kilometers in doorsnede, en kan voor de zwarte gaten die zich in de kernen van sterrenstelsels bevinden zelfs miljoenen kilometers groot zijn. Wellicht is een dergelijke horizon dus een goede plek om te zoeken naar de effecten van de quantumzwaartekracht.

Afbeelding 2. Het centrum van de Melkweg.Een foto van het centrum van ons melkwegstelsel, in het sterrenbeeld Boogschutter. In de buurt van het witte gebied bevindt zich de grootste concentratie van materie. Volgens berekeningen moet zich daar een zwart gat bevinden met een straal van zo’n 40 miljoen kilometer. Foto: NASA.

Naar boven

Symmetrieën

Uit de beschrijving hierboven is waarschijnlijk duidelijk dat we door het bestuderen van de horizon van een zwart gat, niet direct informatie zullen vinden over locale quantumzwaartekrachtseffecten die zich op de schaal van de snaren zelf afspelen. Het zal veel eerder zo zijn dat we globale effecten kunnen zien die zich op grote schaal manifesteren.

Het blijkt dat juist in de holografie zulke globale effecten een belangrijke rol spelen. Wie zich de geschiedenis van het holografisch principe herinnert, zal dit niet verbazen: het principe werd immers al in de jaren ’70 door Gerard ’t Hooft en Leonard Susskind geformuleerd, lang voordat Juan Maldacena een expliciet voorbeeld ervan vond in zijn AdS/CFT-correspondentie! Om holografie op globale schaal te begrijpen, is een microscopisch gedetailleerde theorie helemaal niet nodig.

Wat is er dan wel nodig om holografie op globale schaal te begrijpen? Een heel belangrijk ingrediënt blijkt de notie van een symmetrie te zijn. Voor natuurkundigen is een symmetrie een transformatie van een natuurkundig systeem die een nieuw natuurkundig systeem oplevert dat aan dezelfde natuurwetten voldoet. Een bekend voorbeeld is rotatie: als we het hele heelal 90 graden zouden kunnen draaien, zouden we een nieuw heelal vinden dat even goed aan al onze natuurwetten voldoet. Ook translatie – het verschuiven van alles in de natuur – is een voorbeeld van een symmetrie.

Het ligt voor de hand dat dualiteiten symmetrieën “behouden”. Dat wil zeggen: als iemand twee duale beschrijvingen van een bepaald natuurkundig systeem vindt, verwachten we dat elke beschrijving dezelfde symmetrieën heeft. Dit blijkt voor holografische dualiteiten zoals de AdS/CFT-correspondentie inderdaad het geval te zijn. Maar de relatie is in het voorbeeld van Maldacena nog veel sterker: als we van de quantumzwaartekracht in de anti-de Sitterruimte (AdS) alle mogelijke symmetrieën op een rijtje zetten, blijken we daaruit al te kunnen afleiden wat de overeenkomstige conforme veldentheorie (CFT) is die het systeem beschrijft! Al in 1986, dus nog vóór het verschijnen van het artikel van Maldacena, lieten de fysici David Brown en Marc Henneaux aan de hand van dergelijke symmetrie-argumenten zien dat er een relatie bestaat tussen de AdS-ruimte en conforme veldentheorie. Het resultaat van Maldacena kan dus niet alleen gezien worden als een expliciet voorbeeld van de holografische ideeën van ’t Hooft en Susskind, maar ook als een expliciet voorbeeld van de symmetrie-ideeën van Brown en Henneaux!

Afbeelding 3. Marc Henneaux.Samen met David Brown ontdekte Henneaux dat de symmetrieën van de anti-de Sitterruimte volledig vastleggen wat de duale conforme veldentheorie is.

Naar boven

Kerr-zwarte gaten

Al het bovenstaande geeft ons hints over manieren waarop we ideeën rond quantumzwaartekracht en het holografisch principe in ons eigen heelal zouden kunnen testen. Als we in ons heelal…

1. …locaties kunnen vinden waarvan de quantumzwaartekrachtsbeschrijving vertaald kan worden in een conforme veldentheorie, en…
2. …grootheden kunnen vinden die zowel meetbaar zijn als (in de conforme veldentheorie) uit te rekenen…

…kunnen we de uitkomst van de waarnemingen vergelijken met de uitkomst van de holografische berekening, en zo zien of onze ideeën over quantumzwaartekracht kloppen. Een goede locatie zou dus de horizon van een zwart gat kunnen zijn; een goede grootheid een grootheid die met name door de symmetrieën bepaald wordt.

Het bovenstaande klinkt als een goede opzet voor een onderzoeksprogramma, maar bij het uitwerken van dat programma steekt onmiddellijk een belangrijk probleem de kop op. We hebben in onze beschrijving van de AdS/CFT-correspondentie diverse malen de term “supersymmetrie” laten vallen: één van de symmetrieën die beide theorieën in die correspondentie hebben, is een symmetrie die “materiedeeltjes” (fermionen) en “krachtdeeltjes” (bosonen) verwisselt. Een dergelijke symmetrie zien we in de natuur om ons heen niet – in elk geval niet in systemen met lage energieën. De kans bestaat zeker (en is volgens sommige fysici zelfs erg groot) dat supersymmetrie in hoog-energetische systemen wel degelijk zichtbaar zal zijn, maar voor de locaties in het heelal die we kunnen waarnemen lijkt deze supersymmetrie geen enkele rol te spelen. Het lijkt dus bij voorbaat lastig om een realisatie van Maldacena’s dualiteit in het waarneembare heelal te vinden.

Gelukkig komt juist hier het idee van symmetrieën ons te hulp. Kunnen we in ons heelal geen andere locaties vinden die dan wel niet supersymmetrisch zijn, maar die wel een groot aantal andere symmetrieën hebben, en waarvan we op basis van symmetrieën alleen – net als in het werk van Brown en Henneaux – een duale beschrijving in termen van een conforme veldentheorie kunnen vinden?

Zulke locaties blijken inderdaad te bestaan. Het zijn – niet geheel onverwacht – de horizonnen van zwarte gaten, maar wel van een heel bijzondere klasse van zwarte gaten. De zwarte gaten waar het hier om gaat zijn de zogeheten Kerr-zwarte gaten, vernoemd naar de Nieuw-Zeelander Roy Kerr. Zwarte gaten kunnen niet veel van buitenaf waarneembare eigenschappen hebben, maar een van de eigenschappen die ze wel kunnen hebben en die we kunnen waarnemen is een rotatiesnelheid. Die snelheid blijkt in de relativiteitstheorie bovendien begrensd: een zwart gat van gegeven massa heeft een maximaal mogelijke rotatiesnelheid. Een interessante klasse van zwarte gaten wordt dus gevormd door de zwarte gaten die deze maximale draaisnelheid hebben (of daar in elk geval erg dicht in de buurt komen), en het was Kerr die deze klasse van zwarte gaten als eerste binnen de relativiteitstheorie beschreef.

Afbeelding 4. Kerr-zwarte gaten (artist impression).Een ster draait rond een zwart gat, en draagt daarbij materie over aan het zwarte gat. De invallende materie zal in een spiraal het zwarte gat in vallen, waardoor het zwarte gat zelf ook gaat draaien. Er is een grens aan de draaisnelheid die zo bereikt kan worden; zwarte gaten die met de maximale draaisnelheid draaien heten Kerr-zwarte gaten. Afbeelding: NASA.

Het mooie aan deze Kerr-zwarte gaten is dat ze enorm veel symmetrieën hebben – zoveel, dat de redenering van Brown en Henneaux ook voor deze zwarte gaten gebruikt kan worden om een conforme veldentheorie te vinden die een duale beschrijving van hun fysica moet geven. Kerr-zwarte gaten lijken daarmee een ideale testcase voor onze ideeën over quantumzwaartekracht!

Naar boven

Kerr/CFT aan de sterrenhemel

Zien we aan de sterrenhemel inderdaad Kerr-zwarte gaten? Zwarte gaten die exact de maximale draaisnelheid hebben zijn natuurlijk een puur theoretische constructie, maar er bestaan inderdaad zwarte gaten die deze limiet erg dicht benaderen. Een goed voorbeeld is een dubbelster met de weinig poëtische naam GRS1915+105. Van deze dubbelster, die met name röntgenstraling uitzendt, is één component goed zichtbaar, en kunnen we aan de hand van de beweging van de zichtbare component uitrekenen dat de andere component een zwart gat moet zijn. Uit metingen aan de materie die dit zwarte gat in beweegt kunnen we bovendien afleiden dat de rotatiesnelheid van dit zwarte gat tenminste 98% van de maximale waarde moet zijn.

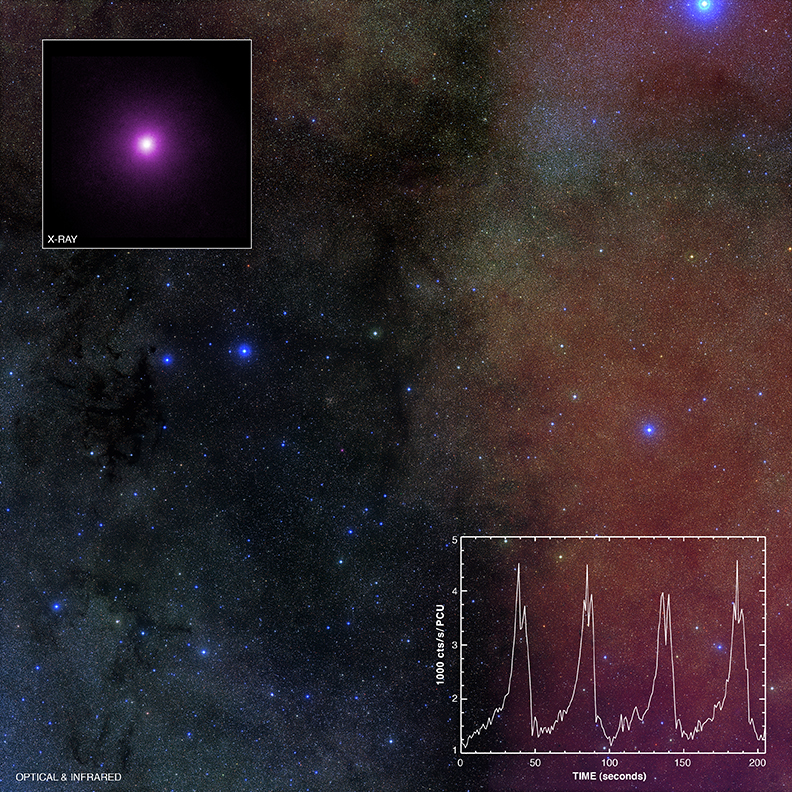
Afbeelding 5. GRS1915+105.Dezelfde afbeelding als bovenaan dit artikel, nu met twee inzet-afbeeldingen. Linksboven het ingezoomde beeld van de zichtbare component van de dubbelster zoals dat in röntgenstraling zichtbaar is. Rechtsonder een grafiek van de variatie van de licht-intensiteit van deze ster. Uit deze variatie kan de rotatiesnelheid van het zwarte gat berekend worden; de uitkomst is dat dat ronddraait met tenminste 98% van de maximaal mogelijke snelheid. Afbeelding: Chandra X-ray Observatory.

Daarmee lijkt de eerste van de twee stappen uit ons mini-onderzoeksplan hierboven voltooid. De uitdaging is nu natuurlijk om een waarneming te bedenken die aan een systeem als GRS1915+105 gedaan kan worden, en die ons iets vertelt over de quantumzwaartekrachtseffecten die ongetwijfeld rond deze dubbelster (preciezer: rond de horizon van het zwarte gat) een rol moeten spelen. Door theoreten wordt hier al hard over nagedacht; met name de onderzoeksgroep van de Amerikaan Andrew Strominger is met vragen zoals deze bezig. (Het was ook Strominger die met zijn team als eerste liet zien dat een Brown-Henneaux-achtige redenering ook voor Kerr-zwarte gaten geldt.) De ontwikkelingen zijn op dit moment nog niet in het stadium dat een exact waarneemvoorstel gedaan kan worden, maar het is niet uit te sluiten dat dat stadium binnen afzienbare tijd bereikt kan worden. Het is natuurlijk ook goed mogelijk dat de cruciale stap juist vanuit de sterrenkunde gezet kan worden: Kerr-achtige systemen worden veel bestudeerd, en roepen ook bij astronomen veel vragen op. Wellicht zal blijken dat juist de technieken van Strominger en zijn collega’s nieuw licht op deze vragen kunnen werpen. Kortom: dit is beslist een interessant onderzoeksgebied om de komende jaren (bijvoorbeeld via de Quantum Universe-site) in de gaten te houden!

Naar boven

In het veertiende artikel in dit dossier zien we hoe twee populaire begrippen uit de moderne natuurkunde, verstrengeling en entropie, samen een nieuw begrip vormen dat een belangrijke rol speelt in het hedendaagse onderzoek naar het holografisch principe.