Quantumfysica (5): De Schrödingervergelijking

In de vier artikelen die tot nu toe in deze serie zijn verschenen, hebben we gezien hoe de quantummechanica een aantal grondbeginselen uit de klassieke natuurkunde op zijn kop zette. Waar we altijd dachten dat natuurkundige verschijnselen ófwel golven ófwel deeltjes zijn, blijken in de quantummechanica beide eigenschappen tegelijk een rol te spelen. Zowel licht als bijvoorbeeld elektronen worden beschreven door golven in de vorm van golffuncties, maar die golven geven kansverdelingen weer die ons vervolgens vertellen waar de kans het grootst is om het licht of het elektron als deeltje aan te treffen.

Afbeelding 1. Golf of deeltje?Is licht een golf of een deeltje? Het is maar hoe je ernaar kijkt! (Afbeelding: Douglas Hofstadter.)

Dit leidt ertoe, zoals we in het vorige artikel gezien hebben, dat we goed moeten nadenken over de precieze interpretatie van klassieke begrippen zoals “golf” en “deeltje” in de quantummechanica. Maar het leidt er ook toe dat de wiskunde waarmee we quantumsystemen beschrijven een stuk ingewikkelder wordt. In dit artikel zullen we die problemen nader omschrijven – zonder daarbij overigens heel diep op allerlei technische wiskundige aspecten in te gaan.

Het belangrijkste verschil tussen rekenen aan een klassiek systeem en rekenen aan een quantumsysteem is het volgende. Een klassiek systeem kan volledig beschreven worden door van al zijn relevante eigenschappen te beschrijven hoe die in de loop van de tijd veranderen. Als we bijvoorbeeld de baan van een kogel willen beschrijven, zijn we in het algemeen geïnteresseerd in de positie (x) en de snelheid (v) van die kogel. Die positie en snelheid veranderen in de loop van de tijd, dus de dynamica van het systeem kan beschreven worden door een tweetal functies, x(t) en v(t).

Afbeelding 2. Een kanonskogel.Om de dynamica van een kanonskogel te kunnen beschrijven, zijn we met name geïnteresseerd in hoe zijn plaats x en snelheid v in de loop van de tijd t veranderen. (Afbeelding: Lance Corporal Samantha L. Jones, USMC)

Voor een quantumsysteem wordt een dergelijke beschrijving beduidend ingewikkelder. Bij een quantumsysteem kunnen we namelijk, zoals we inmiddels weten, op de meeste momenten niet van een exacte plaats of een exacte snelheid spreken. Op elk tijdstip t zal er voor elke plaats x een kans zijn dat het systeem zich daar bevindt. Om het quantumsysteem volledig te begrijpen, moeten we dus een kans (of, in de terminologie uit het vorige artikel, een golffunctie) kennen op elk tijdstip én op elke plek. De golffunctie die de plaats weergeeft, vaak weergegeven met een Griekse hoofdletter Ψ, is dus een functie van tijd én plaats: Ψ(x,t). Op dezelfde manier is er bijvoorbeeld een golffunctie die de (kans op de) snelheid v weergeeft, en die we kunnen schrijven als Φ(v,t).

Kortom: wiskundig komt de stap van klassieke natuurkunde naar quantumfysica overeen met de stap van het werken met functies van alleen de tijd, naar het werken met (golf)functies die van nog meer variabelen afhangen. Een gevolg daarvan is dat we de natuurkundige vragen die we kunnen stellen ook iets zullen moeten aanpassen. Een goede klassieke natuurkundige vraag is bijvoorbeeld: als ik een kogel op een bepaald moment een bepaalde snelheid en positie geef, hoe veranderen die snelheid en positie dan in de loop van de tijd? Het antwoord op die vraag kan berekend worden met behulp van de mechanicawetten van Newton.

In de quantummechanica ziet de analoge vraag er als volgt uit. Als ik de kansverdeling (en dus de golffuncties) van de plaats en snelheid van een systeem op een bepaald moment ken, hoe veranderen de bijbehorende kansen (en dus de golffuncties) dan in de loop van de tijd? Het zal duidelijk zijn dat er, om deze vraag te kunnen beantwoorden, geheel nieuwe natuurwetten nodig zijn. Het vinden van de natuurwetten waaraan de golffuncties uit de quantummechanica voldoen, was een belangrijke zoektocht aan het begin van de 20e eeuw. Het antwoord op de bovenstaande vraag werd uiteindelijk door verschillende natuurkundigen op verschillende manieren beschreven. De meest beroemde formulering is afkomstig van de Oostenrijkse natuurkundige Erwin Schrödinger, die het antwoord in 1925 weergaf in zijn befaamde Schrödingervergelijking.

Afbeelding 3. Erwin Schrödinger.(Auteur foto onbekend.)

Voor wie niet schrikt van een wiskundige vergelijking: in de meest eenvoudige formulering ziet de vergelijking van Schrödinger er als volgt uit:

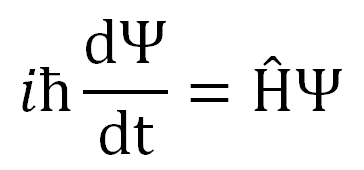
Afbeelding 4. De Schrödingervergelijking.

Het zou te ver voeren om alle wiskundige details van deze vergelijking hier uit te leggen – daarvoor is een volledig eerstejaars universiteitscollege quantummechanica nodig – maar ook zonder die wiskunde kunnen we aan de bovenstaande vergelijking toch al veel interessante zaken aflezen.

Allereerst zien we duidelijk dat de vergelijking iets zegt over golffuncties: zowel links als rechts van het gelijkteken komt het symbool Ψ voor. De Ψ die we hierboven voor de plaats-golffunctie hebben gebruikt is hier overigens een meer algemeen symbool; we zouden een soortgelijke vergelijking evengoed voor de snelheids-golffunctie Φ kunnen opschrijven.

Ten tweede zien we in de linkerhelft van de vergelijking ook het symbool t – voor tijd – staan. Wie wat meer wiskunde beheerst zal ook de d’s herkennen, en zien dat het hier gaat om een tijdsafgeleide: het linkerlid van de vergelijking beschrijft hoe de golffunctie in de loop van de tijd verandert. Dat is natuurlijk precies waar we in onze vragen hierboven in geïnteresseerd waren.

Het linkerlid van de vergelijking bevat verder nog twee andere symbolen. Ten eerste is daar het symbool ħ, dat de constante van Planck (om heel precies te zijn: gedeeld door 2π) weergeeft. Dat die constante in de vergelijking een rol speelt, is natuurlijk niet verrassend. We hebben het hier immers over quantumeffecten, dus we kunnen verwachten dat de belangrijkste constante uit de quantummechanica in de vergelijking voorkomt! Ten slotte zien we het symbool i, dat staat voor een complexe getal “in de imaginaire richting” – zie het vorige artikel. Zoals we in dat artikel al zeiden, gaat quantummechanica eigenlijk over complexe getallen – niet alleen over reële – en hoewel we dit idee verder niet zullen uitwerken, is het dus niet zo vreemd dat ook in de Schödingervergelijking een complex getal voorkomt.

Op deze twee constantes na zegt de linkerkant van de vergelijking dus in woorden: “de verandering van de golffunctie in de loop van de tijd is…” – en dat is precies de informatie waarin we geïnteresseerd zijn. De rechterkant van de vergelijking vertelt ons vervolgens hoe we die verandering kunnen uitrekenen. We zien daar wederom de golffunctie Ψ staan. Met andere woorden: hoe de golffunctie in de toekomst gaat veranderen, hangt af van wat die golffunctie op dit moment is. Dat is niet zo vreemd: waar een kogel in de toekomst naartoe gaat, hangt ook af van waar de kogel op dit moment is.

Afbeelding 5. Erwin Schrödinger.Erwin Schrödinger – en het symbool Ψ voor de golffunctie – op een Oostenrijks bankbiljet van 1000 schilling.

Tenslotte zien we rechts in de vergelijking het symbool Ĥ staan. Het hoedje op de H geeft aan dat het gaat om een zogenaamde operator: Ĥ is geen getal, maar een voorschrift dat ons vertelt hoe we uit de Ψ op dit moment, de toekomstige Ψ kunnen uitrekenen. De notatie Ĥ is een geval van extreme “shorthand” – in de praktijk is het namelijk zo dat deze Ĥ er voor ieder verschillend probleem anders uit zal zien. De ene keer is het genoeg om bijvoorbeeld Ψ te kwadrateren, de andere keer moeten we ook aan de rechterkant van Ψ bepaalde afgeleiden nemen, enzovoort. Kortom: de echte fysica zit hem in de precieze vorm van de operator Ĥ. Wat Schrödinger deed was uitvogelen hoe deze operator er voor elk fysisch systeem uitziet – dat wil zeggen: hij gaf een exact voorschrift om, als we de klassieke bewegingswetten van een systeem kennen, ook de quantumoperator Ĥ uit te rekenen. Daarmee kon vanaf dat moment voor vrijwel elk systeem de quantum-evolutie bepaald worden. Zo konden dus voorspellingen aan quantumsystemen gedaan worden – voorspellingen die natuurlijk vervolgens weer in experimenten getest konden worden. De afleiding van de Schrödingervergelijking was dan ook een zeer belangrijke doorbraak in de ontwikkeling van de quantummechanica.

Nu we een beetje een gevoel hebben voor hoe de quantummechanica erin slaagt om voorspellende berekeningen te doen, wordt het hoog tijd om eens te kijken naar wát die voorspellingen precies zijn, en met name hoe ze verschillen van de voorspellingen die de klassieke natuurkunde doet. Aan de hand van zulke verschillen kunnen we immers experimenteel testen of de quantummechanica het bij het juiste eind heeft. In het volgende artikel zullen we een eerste en heel belangrijk verschil met de klassieke natuurkunde tegenkomen: de onzekerheidsrelatie van Heisenberg.

Dit is het vijfde artikel uit het dossier Quantumfysica. In het zesde artikel bespreken we het onzekerheidsprincipe van Heisenberg.