Quantumfysica (9): Quantumcomputers

Het bekende spreekwoord luidt: één gek kan meer vragen dan duizend wijzen kunnen beantwoorden. In de wiskunde geldt een variatie op hetzelfde thema. Eén gek (of een slimme wiskundige – vaak liggen die twee niet ver uit elkaar) kan een eenvoudige vraag stellen, maar het vinden van het antwoord kan duizenden wiskundigen vervolgens heel lang kosten. Beroemde voorbeelden van zulke schijnbaar eenvoudige wiskundeproblemen zijn de Laatste Stelling van Fermat, die in 1637 werd geformuleerd maar pas in 1994 werd bewezen, en het vermoeden van Poincaré, dat in 1904 werd geformuleerd, maar pas in 2003 werd bewezen.

Afbeelding 1. Pierre de Fermat.De Franse jurist en wiskundige die in 1637 zijn beroemde stelling formuleerde.

In deze voorbeelden duurde het oplossen van de vraagstukken met name zo lang omdat niemand precies wist wat de juiste aanpak was. In andere gevallen is echter precies bekend hoe een probleem opgelost kan worden, maar is die oplossingsmethode erg traag. Een eenvoudig voorbeeld is het volgende. Als u gevraagd wordt om het getal 6 te schrijven als product van twee gehele getallen groter dan 1, vindt u waarschijnlijk snel de oplossing: 6 = 2 × 3. Als u vervolgens gevraagd wordt om het getal 356.519 op dezelfde manier als product van twee gehele getallen groter dan 1 te schrijven, zal het u veel meer tijd kosten om de oplossing te vinden.

De procedure is op zich heel eenvoudig: probeer 356.519 te delen door 2, dan door 3, dan door 4, dan door 5, en ga zo door totdat de uitkomst een geheel getal blijkt te zijn. U kunt het iets slimmer aanpakken door bijvoorbeeld 4 over te slaan: als een getal niet door 2 te delen is, dan is het zeker niet door 4 te delen. Uiteindelijk blijkt het op die manier genoeg te zijn om alleen de priemgetallen als factoren te proberen – maar ook dan is het beantwoorden van deze vraag nog een forse opgave. Met genoeg tijd en geduld zou u uiteindelijk na lang rekenen de oplossing kunnen vinden: 356.519 = 541 x 659.

Het oplossen van deze opgave is erg lastig, maar het bedenken ervan was geen enkel probleem. Ik heb eenvoudigweg twee getallen gekozen (541 en 659), en die met elkaar vermenigvuldigd. Om het probleem lastig te houden, heb ik daarvoor twee priemgetallen gekozen, zodat u niet toevallig een veel eenvoudiger paar van factoren kon vinden. Hoe dan ook, met een rekenmachine is dit probleem in enkele seconden geconstrueerd, maar het oplossen ervan met dezelfde rekenmachine kan wel een uur duren! U kunt zich waarschijnlijk voorstellen dat het probleem praktisch onoplosbaar wordt als we het vervolgens toepassen op getallen van, laten we zeggen, 100 cijfers.

Het zou natuurlijk voor wiskundigen erg interessant zijn als er methodes zouden bestaan om dergelijke ingewikkelde problemen op een veel efficiëntere manier op te lossen. Met wiskundige trucs blijken we in dit geval niet heel ver te komen (of beter gezegd: nog niemand heeft zo’n slimme truc weten te verzinnen), maar we kunnen ons afvragen of de techniek ons hier niet een handje zou kunnen helpen. Computers worden steeds sneller – zou het niet mogelijk zijn om een computer te bouwen die alle mogelijkheden heel snel langsgaat?

Afbeelding 2. De Cray-1-supercomputer.Eén van de eerste supercomputers, gebouwd in 1975. Een moderne telefoon rekent zo’n 50× sneller. Toch zullen ook de snelste gewone computers bepaalde wiskundeproblemen nooit kunnen oplossen. Foto: Clemens Pfeiffer.

In eerste instantie lijkt dit onbegonnen werk. Getallen van 100 cijfers zijn nu eenmaal gigantisch groot. Als we elk getal van 100 cijfers één voor één zouden proberen, maakt het eigenlijk nauwelijks uit hoe snel we dat doen – zelfs met een berekening per Plancktijd (mogelijk de kortst mogelijke tijd waarin we nog zinvol van een “berekening” zouden kunnen spreken) zou een computer nog veel en veel langer dan de huidige leeftijd van het heelal nodig hebben om ook maar in de buurt van dit soort enorme aantallen te komen. Kortom: de berekeningen één voor één doen heeft geen enkele zin.

Zou het niet mogelijk zijn om alle berekeningen tegelijkertijd te doen? Op het eerste gezicht lijkt ook dat onmogelijk: in dat geval zouden we een aantal computers nodig hebben dat zelf weer een getal van 100 cijfers is. Zoveel deeltjes bevinden zich niet eens in het zichtbare heelal – dat aantal wordt geschat op een getal van zo’n 80 cijfers – laat staan dat we zoveel computers kunnen bouwen. Ook deze aanpak lijkt dus hopeloos.

Maar is het niet mogelijk om één computer te bouwen die alle berekeningen als het ware “synchroon” uitvoert? Wie deze serie artikelen over quantummechanica heeft gevolgd, ziet misschien in dat dit niet uitgesloten is. In de quantummechanica is het zoals we gezien hebben mogelijk om een systeem in meerdere toestanden tegelijk te laten zijn. Laten we bijvoorbeeld nog eens kijken naar het elektron dat we ook in het artikel over verstrengeling tegenkwamen. Zo’n elektron heeft een zogeheten spin (grofweg: een draaiing in de bewegingsrichting), en die spin kan twee waarden aannemen, die we “up” en “down” hebben genoemd.

Volgens de quantummechanica hoeft het elektron echter niet volledig in de toestand “up” of volledig in de toestand “down” te zijn. Het elektron kan ook in een superpositie van die twee toestanden zijn: het is dan deels in de toestand “up”, en deels in de toestand “down”. Iets preciezer: het elektron heeft een golffunctie, die aan allebei die toestanden een kans toekent. Pas als we de spin van het elektron meten, kiest het een van de twee toestanden; tot dat moment is het als het ware tegelijk in de toestanden “up” en “down”.

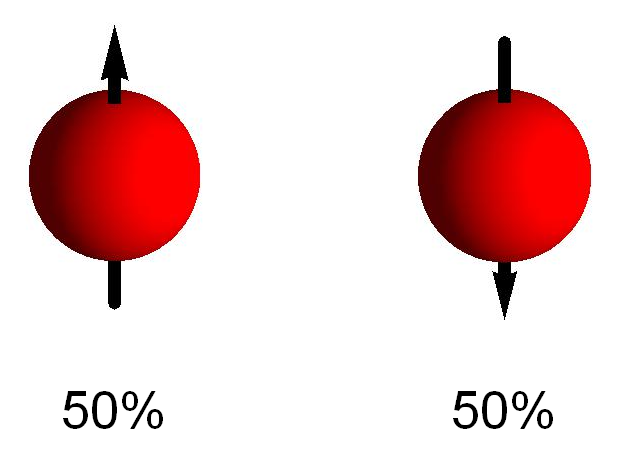
Afbeelding 3. Een superpositie.Een elektron kan op twee manieren “rondtollen”: spin up en spin down. Een quantum-elektron kan ook in een superpositie van die twee toestanden zijn, en bijvoorbeeld voor 50% spin up en voor 50% spin down hebben.

We kunnen dit elektron nu zien als een computerbit. In een gewone computer kan elke geheugeneenheid of bit de waarde 0 of 1 aannemen. Grotere getallen worden gemaakt door meerdere bits te gebruiken: met twee bits zijn bijvoorbeeld de vier combinaties 00, 01, 10 en 11 mogelijk. We kunnen die combinaties de interpretatie van de getallen 0, 1, 2 en 3 geven. Met drie bits kunnen we acht verschillende getallen weergeven, met vier bits zestien, enzovoort.

In een klassieke computer kunnen de bits maar één getal tegelijk weergeven. Als we de bits nu echter vervangen door “quantumbits” (of kortweg: qubits) kunnen we ook een superpositie maken waarin elk getal met een bepaalde kans voorkomt. Als we een elektron zien als zo’n qubit kunnen we bijvoorbeeld “spin down” identificeren met “0”, en “spin up” met 1. Eén qubit kan dan in een superpositie tegelijkertijd de getallen 0 en 1 weergeven; vier qubits kunnen bijvoorbeeld al tegelijkertijd de getallen 0 t/m 15 weergeven. Met wat verder rekenen ontdekken we dat we, om alle getallen met hooguit 100 cijfers tegelijk weer te geven, 336 qubits nodig hebben.

Een slimme quantumcomputer die kan rekenen met dergelijke qubits kan dus tegelijk een getal delen door alle mogelijke getallen met 100 of minder cijfers. Daarmee zijn we er natuurlijk nog niet, want vervolgens moeten we uit de superpositie van mogelijke antwoorden nog het ene antwoord isoleren dat zelf een geheel getal is. Dat getal moeten we vervolgens op een leesbare manier weten weer te geven. Met slimme wiskundige trucs blijkt het echter ook mogelijk te zijn om dit te doen. Kortom: een quantumcomputer kan in theorie het hierboven beschreven wiskundige probleem in één berekening oplossen!

Het “in theorie” is hier heel belangrijk. In de praktijk staat het bouwen van quantumcomputers namelijk nog in de kinderschoenen. Het blijkt niet eenvoudig om op microscopisch niveau met superposities van een groot aantal toestanden om te gaan, en om die superposities ook lang genoeg in stand te houden om ermee te kunnen rekenen. Hieronder zien we in een filmpje Lieven Vandersypen, een onderzoeker uit Delft, die vertelt over zijn onderzoek aan de realisatie van quantumcomputers. Lieven heeft een van de eerste werkende quantumcomputers gebouwd; deze computer was in staat om het in dit artikel genoemde probleem op te lossen voor het getal 15. Met andere woorden, die computer kon berekenen dat 15 = 5 × 3, door alle mogelijke factoren tegelijk te proberen. Technisch staat dit nog heel ver af van het rekenen met getallen van 100 cijfers; in fundamenteel opzicht is het natuurlijk wel een enorme doorbraak!

Niet alleen wiskundigen en natuurkundigen zijn erg geïnteresseerd in quantumcomputers. Ook cryptografen en allerlei veiligheids- en inlichtingendiensten zijn dat. Precies het probleem dat in dit artikel behandeld is, speelt namelijk ook een grote rol in het versleutelen van geheime boodschappen. Een veelgebruikte methode om dat te doen, de zogenaamde RSA-methode, maakt gebruik van paren van enorm grote getallen. Om berichten te versleutelen, is alleen het product van die twee getallen nodig; om het versleutelde bericht vervolgens te kunnen decoderen zijn echter de twee afzonderlijke getallen nodig.

Het voordeel van deze methode is dat het product van de twee getallen (de zoegnoemde public key) aan iedereen bekendgemaakt kan worden. Op die manier kan iedereen versleutelde berichten aan één bepaalde ontvanger versturen. Het decoderen van de berichten kan echter alleen door de ontvanger zelf gebeuren: hij kent immers als enige de twee afzonderlijke factoren (de private key). Deze methode werkt erg goed, zolang het natuurlijk voor een eventuele onderschepper van het bericht niet mogelijk is om het grote getal in zijn twee factoren te ontbinden. Zoals hierboven beschreven kan een quantumcomputer dat wel – zodra quantumcomputers een realiteit worden, zullen veiligheidsdiensten dus snel over moeten stappen op betere manieren van versleuteling!

Wie meer wil weten over quantumcomputers kan op deze website de lesmodule Rekenen met Elektronen vinden. In die module wordt dieper ingegaan op hoe quantumcomputers nu eigenlijk werken, en wordt met behulp van de quantumcomputer-simulatie jquantum ook een programma voor een (virtuele) quantumcomputer geschreven.

Dit is het negende artikel uit het dossier Quantumfysica. In het tiende artikel kijken we nog eens goed naar het kansbegrip in de quantumfysica.