Quantumfysica (4): Golffuncties

In de vorige drie artikelen hebben we gezien dat de bouwstenen van de materie zowel golf- als deeltjeseigenschappen hebben. Licht beschouwen we normaalgesproken als een golf, maar bij het foto-elektrisch effect en de straling van zwarte lichamen zien we ook duidelijk het deeltjeskarakter ervan. Elektronen beschouwen we meestal als deeltjes, maar in het experiment van Davisson en Germer zien we ook de interferentie die typisch is voor golven. De grote vraag is dus: zijn de bouwstenen van de materie nu golven of deeltjes?

Het duurde tot de jaren ’20 van de 20e eeuw voordat natuurkundigen een tevredenstellend antwoord hadden gevonden. Eén van de eersten die dat antwoord duidelijk formuleerde was de Duitse fysicus Max Born. Borns stelling was dat alle bouwstenen van de natuur zowel golven áls deeltjes zijn.

Afbeelding 1. Max Born.

Hoe moeten we die uitspraak interpreteren? Born gaf daar een duidelijk voorschrift voor: hij zei dat de golven uit de quantummechanica gezien moeten worden als kansverdelingen die bepalen hoe groot de kans is om een deeltje ergens aan te treffen. In die zin wordt een deeltje dus beschreven door een golf.

In afbeelding 2 zien we een eenvoudig voorbeeld van een quantummechanische golf geschetst. We noemen een dergelijke quantumgolf ook wel een golffunctie. Waar de golffunctie het grootst is, is de kans om het deeltje aan te treffen het hoogst. Waar de golffunctie het kleinst is, is de kans om het deeltje aan te treffen het laagst. De golffunctie in afbeelding 2 schetst dus een situatie waarin we een grote kans hebben om een deeltje ergens rond een bepaalde plek aan te treffen (al weten we niet helemaal precies waar), en een heel kleine kans om het deeltje ver van die plek af te vinden.

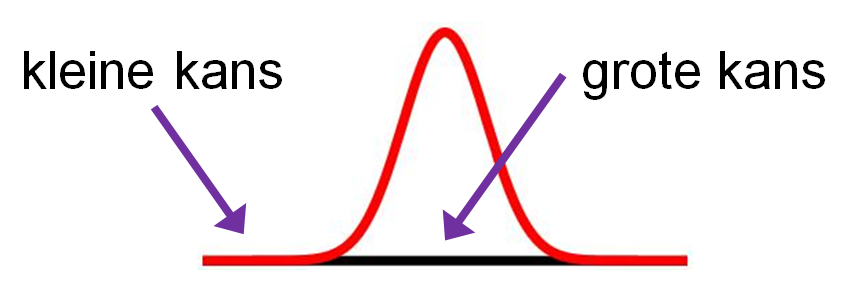
Afbeelding 2. Een voorbeeld van een golffunctie.Waar de golffunctie het grootst is, is de kans om het deeltje aan te treffen het grootst.

Om heel precies te zijn: de bovenstaande beschrijving is slechts een (goede) benadering van wat Born zei. Op twee punten zouden we eigenlijk nog iets preciezer moeten zijn. Voor de liefhebbers daarom hier de kleine lettertes:

1. Het is eigenlijk niet de golffunctie zelf, maar het kwadraat van de golffunctie die de kansverdeling geeft. Dat is niet geheel onlogisch: de uitwijking van een golf (zie afbeelding 3) kan groter dan 0 zijn, maar ook kleiner. Een kans kan echter nooit kleiner dan nul zijn. Het kwadraat zorgt ervoor dat dit probleem wordt opgelost: een kwadraat is immers altijd positief.

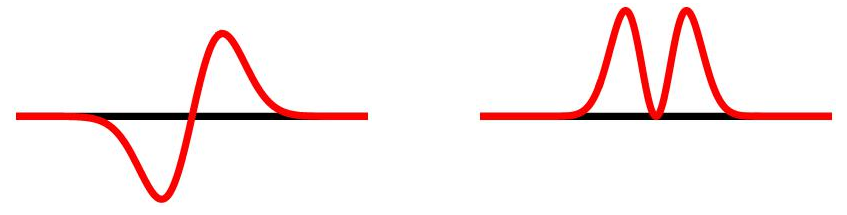
Afbeelding 3. Een golffunctie (links) en het kwadraat ervan (rechts).De waarde van de golffunctie is niet altijd een positief getal. Het kwadraat is dat wel, waardoor het rechterplaatje als een kansverdeling geïnterpreteerd kan worden.

2. Als we de golffuncties goed bestuderen, blijkt dat de waarde van de golffunctie geen “gewoon” getal is, maar een zogeheten complex getal. Het zou te ver voeren om hier een uitgebreide beschrijving van complexe getallen te geven, maar er kan over zulke getallen nagedacht worden als “tweedimensionale getallen”. Waar we een gewoon getal altijd kunnen weergeven als een punt op een getallenlijn, kunnen we een complex getal weergeven als een punt in een plat vlak – zie afbeelding 4. Er blijken betrekkelijk eenvoudige regels te zijn om met zulke complexe getallen te rekenen. Wat voor onze toepassingen belangrijk is om te onthouden, is dat het tweedimensionale karakter van complexe getallen ervoor zorgt dat zulke getallen niet alleen een grootte hebben, maar ook een richting. De grootte in het kwadraat is de kans waar we het hierboven over hadden.

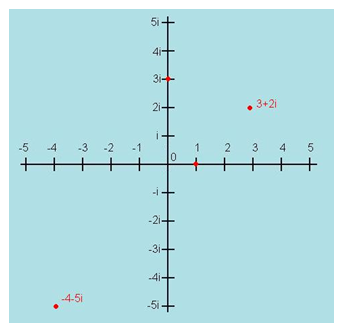
Afbeelding 4. Complexe getallen.We kunnen een complex getal tekenen als een punt in het platte vlak. Op de horizontale as staan de “gewone” (reële) getallen uitgezet. De extra richting wordt meestal met het symbool i (van “imaginair”) aangeduid.

Het is belangrijk dat we beseffen dat het kansbegrip dat in de quantummechanica een rol speelt een fundamenteel kansbegrip is. Daarmee bedoelen we het volgende. In ons dagelijks leven zijn we meestal gewend dat het begrip “kans” iets zegt over onze onwetendheid. Als we met een eerlijke dobbelsteen gooien, weten we dat de kans om een 3 te gooien 1 op 6 is. Dat wil zeggen: gegeven de informatie die we hebben, kunnen we niet bepalen welke uitkomst de worp zal hebben; alle zes de mogelijke uitkomsten zullen in soortgelijke omstandigheden even vaak voorkomen. Als we echter heel precies zouden weten hoe we de dobbelsteen vasthouden, hoe hard we die gooien, hoe ruw het tafeloppervlak is waarover de dobbelsteen rolt, enzovoort, zouden we in principe vooraf exact kunnen uitrekenen welk getal er na de worp boven komt te liggen. In dit geval is het begrip “kans” dus een gevolg van het feit dat we niet exact de situatie kennen.

Bij quantumkansen ligt dat heel anders. Laten we om dat te begrijpen nog eens kijken naar het tweespletenexperiment uit het vorige artikel – zie afbeelding 5. Om het interferentiepatroon op het scherm te kunnen verklaren, moesten we daarin aannemen dat de lichtgolf door allebei de spleten ging – zelfs als we het experiment uitvoeren met maar één lichtdeeltje. In zekere zin gaat het lichtdeeltje dus door allebei de spleten: het is op een gegeven moment voor bijvoorbeeld 50% in de ene spleet, en voor 50% in de andere. Als we bij de spleten een meting zouden doen, zouden we het deeltje in één van de spleten aantreffen, maar als we die meting niet doen, is het deeltje echt “op beide plaatsen tegelijk”. Quantumgrootheden worden om die reden ook wel fuzzy genoemd: die grootheden hebben niet één specifieke waarde, maar allerlei verschillende waardes tegelijk met allerlei verschillende kansen.

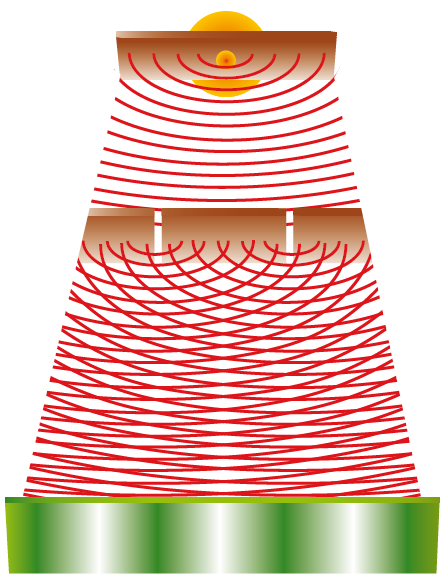
Afbeelding 5. Nogmaals het tweespletenexperiment.De interferentie die we op het scherm zien, vindt altijd plaats, óók als we het experiment met één deeltje tegelijk uitvoeren. Het deeltje is dus “fuzzy”: het gaat door beide spleten tegelijk.

De bovenstaande beschrijving leidt direct tot een nieuwe vraag. In het dagelijks leven ervaren we de wereld namelijk niet als “fuzzy”. We zien voorwerpen op duidelijk bepaalde plaatsen, zien ze bewegen met duidelijk bepaalde snelheden, enzovoort. Ook de wijzers en displays van onze meetinstrumenten geven altijd eenduidige waarden aan – zelfs als die instrumenten een meting aan een quantumsysteem doen. Hoe kan het dat we de quantumonzekerheden in ons dagelijks leven helemaal niet zien?

Dit blijkt een erg diepgaande vraag te zijn, en natuurkundigen zijn het nog altijd niet allemaal eens over het exacte antwoord. De reden is, zoals we hieronder zullen zien, dat deze vraag deels tot het domein van de filosofie hoort, en niet tot dat van de natuurkunde. Laten we drie mogelijke antwoorden, die elk de nodige aanhangers hebben, op een rijtje zetten.

1. Het “klassieke” antwoord is als volgt: zodra we een meting doen aan een quantumsysteem “stort de golffunctie in”. Dat wil zeggen: op dat moment kiest het systeem één van de vele mogelijke toestanden, waarbij elke toestand de door de golffunctie beschreven kans heeft om gekozen te worden. Een groot nadeel van deze interpretatie is dat niet duidelijk is wat precies een meting is: kan alleen een mens een meting doen, of kan een dier dat ook, of zelfs een apparaat? Is er een “bewustzijn” nodig om een meting te doen? Het moge duidelijk zijn dat we met dergelijke vragen al snel het terrein van de natuurkunde verlaten.
2. Een ander populair antwoord is dat quantumeffecten kleiner worden naarmate het systeem dat we beschrijven complexer wordt. Om metingen te doen hebben we in het algemeen erg complexe apparaten nodig, die bestaan uit gigantische aantallen atomen. Die atomen, die de toestand weergeven van het systeem dat we bestuderen (bijvoorbeeld de positie van een deeltje) zijn zelf ook quantumdeeltjes, en in feite bekijken we bij een meting dus nooit één deeltje, maar altijd een enorm complex systeem van quantumdeeltjes. De stelling (die in eenvoudige gevallen ook bewezen kan worden) is nu dat de quantumgolven van dergelijke complexe systemen altijd heel erg “gelocaliseerd” zijn: zo’n golffunctie heeft een heel smalle, scherpe piek, en van een dergelijk groot systeem is dus met grote nauwkeurigheid bepaald in welke toestand het is. Op die manier zou verklaard kunnen worden waarom we in het dagelijks leven nooit metingen kunnen doen waar een “fuzzy” antwoord uitkomt. Het grote probleem is om deze “localisatie” (ook wel coherentie genoemd) ook voor algemene systemen te bewijzen.
3. Een laatste populaire interpretatie is dat quantumkansen helemaal niet fundamenteel zijn, maar wel degelijk gebaseerd op onze onwetendheid. Er zouden in zo’n geval “verborgen variabelen” zijn die, als we hun waarden zouden kennen, precies zouden vertellen in welke van de mogelijke quantumtoestanden een systeem is. Een probleem met deze interpretatie is dat we in een dergelijke theorie ook moeten kunnen verklaren hoe de quantum-lichtgolf in het tweespletenexperiment toch door beide spleten tegelijk kan lijken te gaan. Ook dit is een probleem dat voor specifieke voorbeelden opgelost kan worden, maar waarvoor geen algemeen geldende oplossing bekend is.

Dit zijn drie populaire opvattingen, maar er zijn er nog veel meer. Kortom: we weten het antwoord op de vraag “hoe worden quantumkansen in een meting gerealiseerd” niet precies. Gelukkig is, zoals we hierboven al zeiden, deze vraag voor een groot deel filosofisch van aard. We weten namelijk wél hoe we de quantumkansen moeten uitrekenen, en kunnen daardoor exacte voorspellingen van de uitkomsten van experimenten doen. Die uitkomsten zullen altijd een kansaspect in zich hebben, maar door het experiment vaak te herhalen kunnen we verifiëren dat de berekende kansen inderdaad juist zijn. Hoewel de interpretatiekwesties rond de quantummechanica dus filosofisch erg interessant zijn, zullen we ze voor de rest van deze artikelenserie achter ons laten, en alleen de fysische voorspellingen van de quantumtheorie verder bestuderen.

Dit is het vierde artikel uit het dossier Quantumfysica. In het vijfde artikel komen we de misschien wel belangrijkste vergelijking uit de hele quantumfysica tegen: de Schrödingervergelijking.