Quantumfysica (7): Verstrengeling

Zoals we inmiddels weten, gaat quantummechanica over kansen. Een quantummechanisch systeem hoeft niet in één specifieke toestand te zijn: het kan in zekere zin in verschillende toestanden tegelijk zijn. De golffunctie die bij het systeem hoort, kent aan elk van die mogelijke toestanden een kans toe. Zo kan een deeltje bijvoorbeeld voor 50% (dus met 50% kans) op positie A zijn, en voor 50% op positie B. Een dergelijke toestand noemen we een superpositie. Pas wanneer we de positie van het deeltje meten, verandert deze situatie en “stort de golffunctie ineen” tot een functie die ofwel aan positie A 100% kans toekent, ofwel aan positie B. Met andere woorden: door het doen van de meting “dwingen we het deeltje te kiezen”, en pas op dat moment is het deeltje niet meer in een superpositie, maar ofwel op plaats A, ofwel op plaats B.

Afbeelding 1. Verstrengeling.Als twee touwen verstrengeld zijn, kunnen we ze wel samen verplaatsen, maar niet afzonderlijk. Met andere woorden: zodra we de positie van het ene touw weten, weten we ook de positie van het andere. Afbeelding: William B. Folsom, NMFS.

Deze eigenschap is voor afzonderlijke deeltjes al bijzonder, maar zodra we het hebben over paren van deeltjes wordt het nog veel interessanter. Om dit te begrijpen is het goed om te kijken naar heel eenvoudige systemen, die maar in een klein aantal toestanden kunnen zijn. Een voorbeeld van zo’n systeem is een elektron. Een elektron blijkt namelijk niet alleen eigenschappen zoals een plaats en een snelheid te hebben, maar ook een eigenschap die we spin noemen.

De exacte wiskunde achter het begrip spin is vrij ingewikkeld, dus we volstaan hier met een wat intuïtievere beschrijving. Over spin kunnen we nadenken als over het rondtollen van het elektron: hoewel een elektron een puntdeeltje is, en dus eigenlijk niet kan ronddraaien, blijkt het zich toch te gedragen alsóf het rondtolt. In iets meer technische termen: het elektron heeft een zogenaamd impulsmoment – een eigenschap die bij botsingen met voorwerpen die wél kunnen draaien, overgedragen kan worden, en die zich dan vertaalt in het rondtollen van dat tweede voorwerp.

Het blijkt echter niet mogelijk te zijn om een elektron een willekeurige hoeveelheid impulsmoment te geven: er is een alleen een vaste, heel kleine hoeveelheid “draaiing”, gemeten ten opzichte van de bewegingsrichting, die we aan het elektron mee kunnen geven. Dat houdt in dat een elektron maar twee mogelijke draaiingstoestanden heeft: gezien in de bewegingsrichting kan het een heel klein beetje rechtsom “tollen”, of een heel klein beetje linksom. Elk elektron kan dus in precies twee impulsmoment-toestanden zijn. We noemen die twee toestanden spin up en spin down.

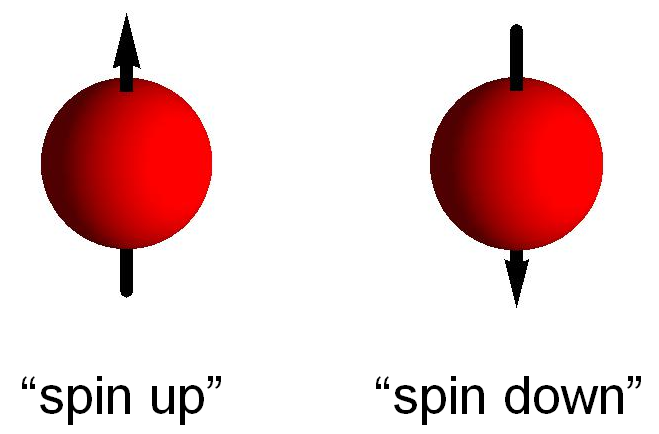
Afbeelding 2. Spintoestanden van een elektron.Een elektron kan op precies twee manieren “rondtollen”. We kunnen die twee manieren aangeven door middel van een pijltje (het elektron draait ten opzichte van dat pijltje bijvoorbeeld rechtsom), en noemen de twee toestanden spin up en spin down.

Nu is het quantummechanisch natuurlijk zo dat een elektron niet voor 100% in de spin up-toestand of voor 100% in de spin-downtoestand hoeft te zijn. Ook hier zijn weer superposities mogelijk: het elektron kan bijvoorbeeld voor 30% (met een kans van 30%) spin up hebben, en voor 70% spin down. Sterker nog: wanneer we een elektron maken in een botsingsexperiment waarin oorspronkelijk geen draaiing aanwezig is, zal het elektron geen enkele reden hebben om een bepaalde kant op te tollen, en zal het ontstane elektron dus in het algemeen in een toestand zijn waarin het voor 50% spin up heeft, en voor 50% spin down. (Zie afbeelding 3.)

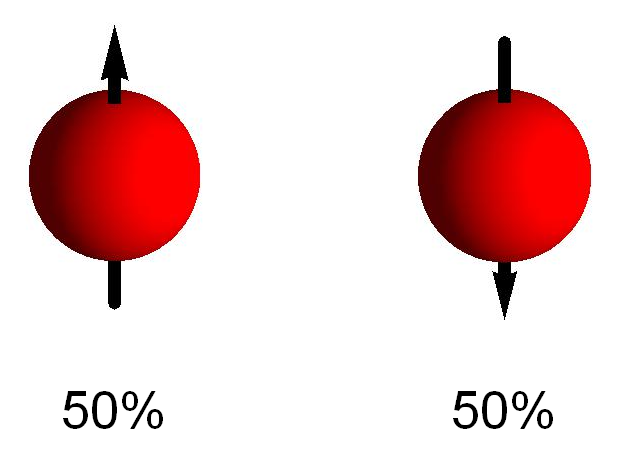
Afbeelding 3. Een elektron zonder voorkeursdraairichting.Als een elektron ontstaat in een experiment waar vooraf geen draaiing aanwezig is, zal het in het algemeen in een toestand zijn waarin het voor 50% spin up heeft, en voor 50% spin down.

Zoals gezegd zijn we in dit artikel met namen geïnteresseerd in paren van deeltjes. Laten we nu dus eens kijken naar een botsingsexperiment waarin niet alleen een elektron ontstaat, maar een elektron en een anti-elektron, of positron. Dit paar van deeltjes kan nu in vier basistoestanden zijn: beide deeltjes kunnen spin up hebben, beide deeltjes kunnen spin down hebben, het elektron kan spin up hebben en het positron spin down, en omgekeerd. Quantummechanisch gezien zijn superposities van al deze toestanden mogelijk, dus al met al geeft de golffunctie van dit systeem ons vier kansen – één voor elk van de vier mogelijkheden. In afbeelding 4 zien we een voorbeeld van zo’n kansverdeling.

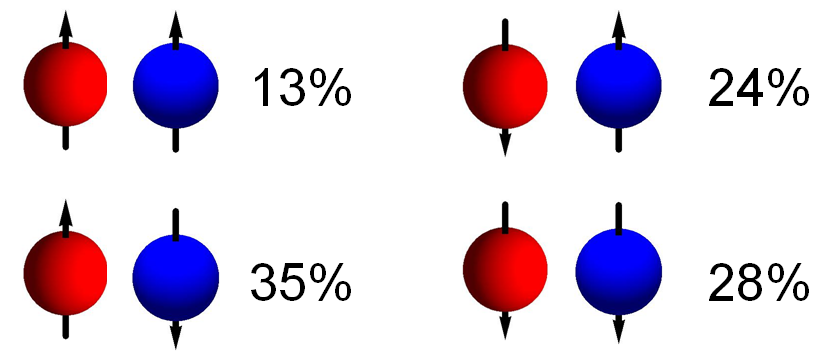
Afbeelding 4. Een elektron en een positron.Het elektron (rood) en het positron (blauw) kunnen elk spin up of spin down hebben. De golffunctie die dit paar van deeltjes beschrijft geeft ons dus vier kansen – één voor elke mogelijke situatie. Merk op dat de vier kansen samen natuurlijk optellen tot 100%.

Een toestand als in afbeelding 4 zal met de nodige technische foefjes zeker te maken zijn, maar als het elektron en het positron bij een botsingsexperiment tegelijk in een vacuüm ontstaan zijn niet alle vier de basistoestanden mogelijk. In dat geval zal het altijd zo zijn dat het elektron rechtsom tolt als het positron linksom tolt, en andersom. Met andere woorden: beide deeltjes hebben dan een tegengestelde spin. Verder zal zo’n experiment meestal geen voorkeursuitkomst hebben, en kunnen we dus verwachten dat de kans die hoort bij elk van de twee mogelijke basistoestanden 50% is. Met andere woorden: in een eenvoudig botsingsexperiment zal een toestand ontstaan zoals die is weergegeven in afbeelding 5.

Afbeelding 5. Een elektron en een positron.Als de twee deeltjes in een botsingsexperiment in een vacuüm ontstaan zullen ze tegengestelde spin hebben. Dat laat slechts twee basistoestanden over; in het algemeen zal de kans voor elk van deze toestanden even groot zijn.

De toestand die nu is ontstaan noemen we een verstrengelde toestand. De reden voor deze naam is als volgt. Als we kijken naar één van de twee deeltjes – bijvoorbeeld het elektron – hebben we geen enkele informatie over de spintoestand van dat deeltje. Bij een meting hebben we 50% kans om voor het elektron “spin up” te meten, en 50% kans om “spin down” te meten. Zodra we een dergelijke meting gedaan hebben, stort de golffunctie echter in – één van de twee mogelijke uitkomsten wordt gekozen – en vanaf dat moment weten we ook voor 100% zeker in welke spintoestand we het andere deeltje zullen aantreffen. Een meting aan het ene deeltje bepaalt dus de toestand van het andere deeltje! We kunnen dit vergelijken met een situatie waarin twee touwen met elkaar verstrengeld zijn: zodra iemand ons vertelt dat het ene touw in New York is, weten we direct dat het andere touw ook in New York is. Het bijzondere in het quantumgeval is natuurlijk dat de combinatie van de twee touwen ook voor 50% in New York en voor 50% in Amsterdam kan zijn; zodra we dan de plaats van het ene touw meten en de golffunctie instort, is ook het andere touw direct op dezelfde plaats!

Het idee van verstrengeling leidt tot allerlei interessante vraagstukken. Het broemdste van deze vraagstukken werd opgeworpen door Albert Einstein en twee van zijn collega’s, Boris Podolsky en Nathan Rosen. Zij schreven een artikel over een vraag die later bekend zou komen te staan als de Einstein-Podolsky-Rosenparadox of EPR-paradox. Hun vraag ging over een iets ander systeem, maar is in termen van ons experiment als volgt te vertalen. Stel dat we het bovenstaande experiment doen, maar voordat we de toestand van het elektron meten, stoppen we het positron in een doos, en schieten het met een raket naar de maan. Als de bovenstaande redenering klopt, kunnen we een meting aan het elektron doen, en heeft dat onmiddellijk een gevolg voor de toestand van het positron op de maan. Einstein vond dit een heel vreemde situatie – hij had immers zelf bewezen (zie het dossier over relativiteitstheorie) dat het onmogelijk was om informatie sneller dan het licht te verzenden! Een signaal van het elektron zou er dus ruim een seconde over moeten doen om op de maan te belanden. Hoe kan het positron dan onmiddellijk van toestand veranderen?

Afbeelding 6. “Einstein attacks quantum theory”.Een kop uit de New York Times van 4 mei 1935, over het artikel dat Einstein met Podolsky en Rosen schreef.

De uiteindelijke oplossing van deze paradox is als volgt. Hoewel het positron op de maan onmiddellijk van toestand verandert als we op aarde een meting aan het elektron doen, kan dit experiment op geen enkele manier gebruikt worden om informatie over te zenden. We kunnen immers vooraf met geen mogelijkheid bepalen wat de uitkomst van het experiment op aarde zal zijn. We kunnen dus niet vooraf besluiten om “spin up” te meten, en op die manier “spin down” naar de maan sturen. Met andere woorden: het is op deze manier niet mogelijk om gebeurtenissen op de maan te beïnvloeden. Einstein had met zijn relativiteitstheorie laten zien dat een dergelijke instantane invloed onmogelijk was, en dat bleef ook in de quantumtheorie zo. Ook in andere (gedachten-) experimenten blijkt het onmogelijk te zijn om de quantummechanica te gebruiken om sneller dan het licht informatie over te zenden. De quantummechanica en de relativiteitstheorie zijn dus (gelukkig!) niet met elkaar in tegenspraak.

Dit is het zevende artikel uit het dossier Quantumfysica. In het achtste artikel zullen we zien hoe klassiek onmogelijke processen in de quantummechanica opeens mogelijk worden.