In het vorige artikel hebben we gezien dat het rekenen met kansen in de quantummechanica een behoorlijke klus kan zijn. De toestand van een “klassiek” deeltje op een bepaald moment kunnen we weergeven door zijn plaats en snelheid te beschrijven. In onze driedimensionale ruimte wil dat zeggen dat we drie plaatscoördinaten en drie snelheidscoördinaten moeten geven – in totaal zes getallen.
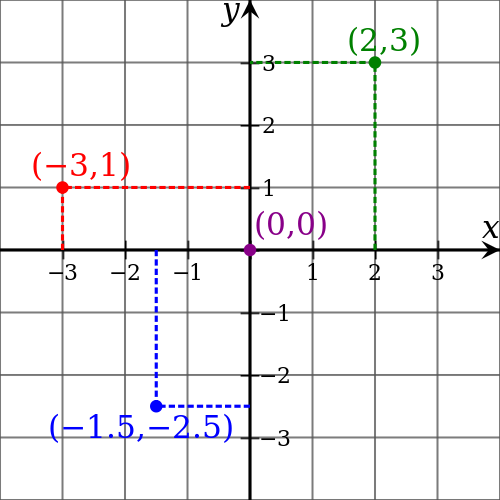
Afbeelding 1. Coördinaten.Om een punt in een tweedimensionaal vlak weer te geven, hebben we twee coördinaten nodig. Om de positie van een deeltje in drie dimensies te beschrijven, is nog een coördinaat in de derde richting nodig. Hetzelfde geldt voor snelheden, die immers ook een grootte en een richting hebben. Afbeelding: K. Bolino.
Voor een quantumdeeltje moeten we echter voor elke mogelijke plaats en snelheid de bijbehorende kans beschrijven. Aangezien er oneindig veel plaatsen en snelheden mogelijk zijn, komt dat neer op oneindig veel getallen. De beschrijving van de toestand van een quantumdeeltje bevat dus in zekere zin oneindig veel meer informatie dan de toestand van een klassiek deeltje.
In meer wiskundige termen kunnen we de situatie als volgt omschrijven. Voor het weergeven van de positie en snelheid van een klassiek deeltje zijn zes getallen nodig. Voor het weergeven van de positie en snelheid van een quantumdeeltje is een functie van zes variabelen nodig. Deze functie zijn we al eerder tegengekomen: het is de golffunctie die de toestand van het deeltje beschrijft.
Daarmee lijkt de situatie al flink gecompliceerd, maar het rekenen met functies is iets wat wiskundigen goed onder de knie hebben. Sinds de tijd van Isaac Newton weten we hoe we operaties zoals differentiëren en integreren op functies moeten toepassen, en met behulp van die operaties is het geen probleem om met de golffuncties van de quantummechanica te rekenen en uiteindelijk de verwachte uitkomsten van experimenten te vinden.
Maar hoe zit het in het geval waarin de “klassieke” grootheid waarin we geïnteresseerd zijn zelf al een functie is? Dat is niet zo’n ongebruikelijke situatie als het op het eerste gezicht lijkt. Denk bijvoorbeeld aan het begrip temperatuur. De temperatuur in een kamer is niet op elke plek exact hetzelfde. In de buurt van een verwarming is de temperatuur iets hoger dan gemiddeld; in de buurt van een raam iets lager. Om de exacte temperatuurverdeling weer te geven, moeten we op elk punt in de kamer de temperatuur beschrijven. De temperatuur in de kamer is dus zelf een functie, en er zijn oneindig veel “klassieke” configuraties denkbaar.
Een ander voorbeeld is een elektromagnetische veld. Zo’n veld heeft een grootte en een richting, die op elk punt in de ruimte anders kunnen zijn. Ook om dit veld te beschrijven hebben we dus oneindig veel gegevens nodig, wederom in de vorm van functies. En ook hier gaat het alleen nog maar om de klassieke beschrijving. Dergelijke grootheden, die klassiek op elk punt in de ruimte (en op elk tijdstip) beschreven kunnen worden door een functie, worden net als in het elektromagnetische geval ook in meer algemene termen velden genoemd. Ook als we het over temperatuur hebben, kunnen we dus spreken van een “temperatuurveld”.

Afbeelding 2. Het elektromagnetische veld.Het elektromagnetische veld heeft op elk punt in de ruimte een grootte en een richting. Dit kan bijvoorbeeld aangetoond worden door ijzervijlsel op een vel papier te strooien, en een magneet onder het papier te houden. Afbeelding: Newton Henry Black.
Zoals gebruikelijk verbindt de quantumtheorie aan elke klassieke mogelijkheid een kans. Maar nu zijn er al oneindig veel klassieke variabelen (de grootte van het veld op elk punt in de ruimte), en aan elk van de oneindig veel waarden van die die oneindig veel variabelen samen hebben, kent de quantummechanica een kans toe. Anders geformuleerd: de golffunctie is een functie, die aan elke veldconfiguratie – zelf weer een functie – een kans toekent. De golffunctie is dus een “functie van functies”!
Als het bij al deze oneindigheden begint te duizelen, is dat geen vreemde reactie. Sterker nog: ook voor wiskundigen geldt dat. Het rekenen met functies van functies – ook wel functionalen genoemd – is vele malen lastiger dan het rekenen met gewone functies. Operaties zoals het integreren van een functionaal zijn zelfs vandaag de dag nog altijd niet op een fatsoenlijke manier door wiskundigen te definiëren!
Het rekenen aan quantumvelden lijkt daarmee onbegonnen werk. In zekere zin is het dat ook: zoals gezegd is de precieze wiskunde achter deze zogeheten quantumveldentheorie nog altijd niet bekend. Gelukkig heeft dat natuurkundigen er niet van weerhouden om toch allerlei methoden te bedenken om met quantumvelden om te gaan. De eerste die een dergelijke goed functionerende methode bedacht, was de bekende Amerikaanse natuurkundige Richard Feynman. Hij bedacht een manier om de resultaten van quantumveldenberekeningen stap voor stap te benaderen. Hoewel het exacte antwoord zelden berekend kan worden, kan het antwoord met de methode van Feynman wel erg goed – en soms zelfs willekeurig goed – benaderd worden.

Afbeelding 3. Richard Feynman (1918-1988).De Amerikaanse natuurkundige Richard Feynman bedacht een overzichtelijke manier om berekeningen te doen aan de kansprocessen in de quantumveldentheorie. Foto: The Nobel Foundation.
Het zou veel te ver voeren om de wiskundige trucs van Feynman hier in detail uiteen te zetten. Het leuke is echter dat die trucs schematisch weergegeven kunnen worden in een aantal diagrammen, en dat die diagrammen een heel duidelijke fysische interpretatie hebben. Het idee van Feynman was grofweg als volgt. Zodra er sprake is van een veld, is er ook sprake van fluctuaties in dat veld – oftewel: van golven. We hebben al eerder gezien dat golven en deeltjes in de quantummechanica nauw met elkaar verbonden zijn, en dat geldt ook in dit geval. In plaats van in termen van golfprocessen, kunnen we over de fluctuaties in een veld ook nadenken in termen van deeltjesprocessen. Dat neemt de oneindigheden in de berekeningen niet weg – er zijn nog steeds oneindig veel van dergelijke processen mogelijk – maar het geeft wel een goede manier om de processen te classificeren.
Wat Feynman ontdekte, was namelijk dat lang niet al deze deeltjesprocessen een even grote kans hebben. Hoe minder er in een deeltjesproces gebeurt, hoe groter de kans op dat proces is. Om dat idee kwantitatief te maken, voerde Feynman een diagramnotatie in die tegenwoordig bekend is onder zijn naam: Feynmandiagrammen. Een Feynmandiagram is een grove schets van een type proces, waarbij de paden die de deeltjes in het proces afleggen in de ruimte getekend worden. In afbeelding 4 zien we bijvoorbeeld twee van dergelijke processen. Traditioneel “lezen” we dergelijke diagrammen van links naar rechts. In het linker proces zien we twee deeltjes die links in het diagram beginnen, na enige tijd botsen, samen als één nieuw deeltje verder vliegen, waarna dat deeltje nog iets later weer uiteenvalt in twee deeltjes. Rechts zien we een veel ingewikkelder proces dat ook begint en eindigt met twee deeltjes, maar waar tussendoor allerlei botsingen en vervalsprocessen plaatsvinden.
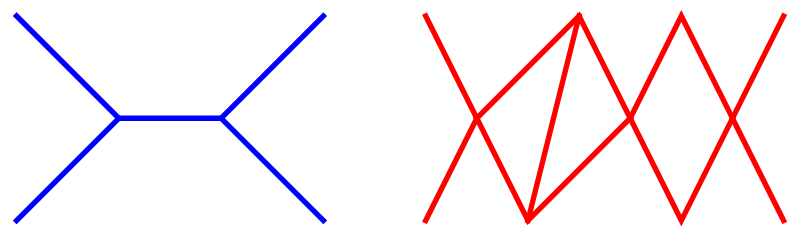
Afbeelding 4. Twee Feynmandiagrammen.In het linker diagram komen twee deeltjes samen om een nieuw deeltje te vormen, dat even later weer uiteenvalt. Het rechter diagram heeft dezelfde begin- en eindproducten, maar beschrijft een veel ingewikkeldere opeenvolging van processen.
Het inzicht van Feynman was nu dat een ingewikkelder proces waarin veel meer interacties plaatsvinden, zodat er meer “kruispunten” en meer “lussen” in het diagram voorkomen, een veel kleinere kans heeft. Daardoor draagt zo’n proces ook veel minder bij aan de quantumberekeningen. Als we een uitkomst van een quantumberekening willen benaderen, kunnen we dus beginnen met het rekenen aan de eenvoudigste processen, zoals dat links in afbeelding 4, en vervolgens het aantal kruispunten en lussen steeds groter maken tot we het antwoord dat we zoeken voldoende dicht zijn genaderd.
Daarmee is het rekenen aan de quantumveldentheorie beslist nog geen trivialiteit geworden. Eén Feynmandiagram staat immers nog altijd voor oneindig veel verschillende processen. Het diagram is immers maar een schets: de verschillende interacties kunnen nog op oneindig veel verschillende plekken plaatsvinden, en de deeltjes kunnen tussen de interacties oneindig veel verschillende snelheden hebben. Maar elk van die plaatsen en snelheden kan worden weergeven door slechts drie getallen. Met andere woorden: we hebben de overdaad aan variabelen teruggebracht tot een eindig aantal variabelen per diagram, en hiermee kan door wiskundigen gerekend worden. Kortom: het probleem is behapbaar geworden, en met behulp van de methodes van Feynman (en allerlei verfijningen die in de jaren daarna nog bedacht zijn) kan de quantumveldentheorie gebruikt worden om met grote nauwkeurigheid voorspellingen te doen. Bij vrijwel alle grote moderne experimenten in de deeltjesfysica (denk aan de deeltjesversneller op het CERN waarmee recent het Higgs-deeltje ontdekt is) spelen dergelijke berekeningen in de quantumveldentheorie een cruciale rol.
Met de invoering van Feynmandiagrammen leken de oneindigheden in de quantumveldentheorie onder controle. Al snel werd echter duidelijk dat zelfs met de methode van Feynman bepaalde quantumveldentheorieën nog altijd tot onjuiste, oneindig grote resultaten leidden. Om ook dit probleem op te lossen, was een geheel nieuwe methode nodig. We zullen in het komende artikel zien wat het probleem precies was, hoe het werd opgelost, en welke belangrijke rol twee Nederlandse natuurkundigen in die oplossing speelden.
Dit is het elfde artikel uit het dossier Quantumfysica. Het twaalfde artikel gaat over renormalisatie.