In de vorige twee artikelen hebben we de quantumveldentheorie beschreven – het raamwerk waarbinnen veel van de moderne deeltjesfysica geformuleerd is. Het belangrijkste grondbeginsel van deze theorie is, zoals de naam al zegt, dat fysische grootheden op microscopisch niveau kunnen worden beschreven door velden. Dat geldt voor krachten – denk aan het elektromagnetische veld dat de elektrische en magnetische krachten overbrengt – maar ook voor deeltjes. We hebben immers al in het derde artikel in deze serie gezien dat deeltjes ook beschreven kunnen worden als golven. “Datgene wat golft” is het bij het deeltje behorende veld. Er is dus een elektronveld (iets anders dan het elektromagnetische veld!), een neutrinoveld, enzovoort.

Afbeelding 1. De proef van Young.De proef van Young met een zeer kleine hoeveelheid licht – het beroemde voorbeeld waaruit blijkt dat quantumverschijnselen tegelijkertijd door golven en door deeltjes beschreven worden. Zie artikel 3 voor de details. Afbeelding: A. Tonomura.
Het omgekeerde geldt ook. De golven in de krachtvelden kunnen op hun beurt gezien worden als deeltjes. Zo wordt het deeltje dat hoort bij het elektromagnetische veld, en dat dus de elektromagnetische kracht overdraagt, het foton genoemd. “Foto” is het Griekse woord voor licht. Deze benaming is niet zo vreemd als we bedenken dat licht niets ander is dan een golf in het elektromagnetische veld. Het foton is dus het bijbehorende deeltje, zoals we ook al in artikel 3 bespraken toen we de proef van Young tegenkwamen.
| Veld | Deeltje | Soort |
| Elektromagnetische veld | Foton | “kracht” |
| Elektronveld | Elektron | “deeltje” |
De twee voorbeelden die we besproken hebben, staan in de tabel hierboven nog eens samengevat. Bij het bekijken van deze tabel komt een belangrijke vraag naar voren. Als we zowel “krachten” (zoals elektrische en magnetische krachten) als “deeltjes” (zoals elektronen) kunnen beschrijven door middel van een veld óf een deeltje – wat is dan het verschil tussen deze twee? Wat maakt dat we sommige grootheden in de natuur ervaren als krachten, en andere grootheden als deeltjes?
Ook dit is een vraag waarop in de jaren ’40 van de vorige eeeuw (een belangrijk decennium voor de quantumfysica!) het antwoord werd gevonden. Het antwoord bleek te liggen in de zogenaamde statistiek van de deeltjes. Met die term duiden we het gedrag van de deeltjes aan als ze met grote aantallen zijn. Een voorbeeld maakt dit begrip “statistiek van deeltjes” waarschijnlijk duidelijker.
Stel dat iemand ons de volgende vraag stelt. Er is een trap met tien treden, en er zijn drie personen: A, B en C. In hoeveel verschillende opstellingen kunnen deze personen op de trap staan?
Een voor de hand liggende manier om het antwoord uit te rekenen is de volgende. We laten eerst persoon A een tree kiezen om op te staan. Hij of zij kan daarvoor uit tien verschillende treden kiezen. Als hij eenmaal een tree bezet heeft, laten we persoon B een tree kiezen – dat kan dan nog op 9 verschillende manieren. Tenslotte kiest persoon C een van de overgebleven 8 treden. Er zijn dus in totaal 10 × 9 × 8 = 720 verschillende opstellingen mogelijk.
De oplettende lezer heeft misschien gemerkt dat we bij het berekenen van dit antwoord een aanname hebben gemaakt – namelijk, dat twee personen niet op dezelfde tree mogen staan. In de oorspronkelijke vraag is dit echter nergens aangegeven. Als we aannemen dat het gaat om een heel brede trap – de Spaanse trappen in Rome, bijvoorbeeld – is er weinig reden om aan te nemen dat de personen niet op dezelfde tree zouden kunnen staan. In dat geval heeft persoon B dus de keuze uit alle 10 de treden, en persoon C eveneens. Er zijn dan 10 × 10 × 10 = 1000 verschillende opstellingen mogelijk.

Afbeelding 2. De Spaanse Trappen.Op bijvoorbeeld een ladder kan op elke tree normaalgesproken maar één persoon staan. Op sommige trappen, zoals hier, kunnen echter heel veel personen tegelijk op dezelfde tree staan. Afbeelding: Wikipediagebruiker Arnaud 25.
Kortom: om de vraag goed te formuleren, moeten we aangeven of twee personen op dezelfde tree kunnen staan. Iets meer natuurkundig geformuleerd: we moeten aangeven of twee personen zich in dezelfde toestand kunnen bevinden.
Precies hetzelfde geldt als we het hebben over quantummechanische deeltjes. Voor zulke deeltjes is vaak een beperkt aantal toestanden mogelijk. Het bekendste voorbeeld is een elektron dat rond een atoomkern cirkelt, en waarvan de golflengte precies een geheel aantal maal in de baan moet passen zodat het elektron zichzelf niet “uitdooft”. De vraag is nu: kunnen twee verschillende deeltjes zich in precies dezelfde toestand bevinden, of kunnen ze dat niet? Het antwoord op deze vraag wordt de statistiek van de deeltjes genoemd.
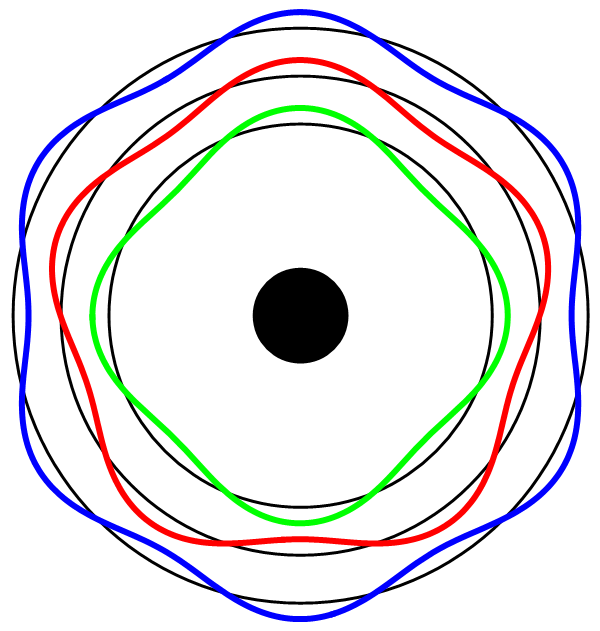
Afbeelding 3. Een atoom.Een atoom is een voorbeeld van een quantummechanisch systeem met een beperkt aantal toestanden. De elektronen hebben een vaste golflengte, en kunnen zich alleen bevinden in banen waar hun golflengte een geheel aantal malen in de baan past. We zien hier voorbeelden van golven waarvan de golflengte 4, 5 en 6 maal in de baan past.
Er blijken, net als in ons voorbeeld met de trap, voor quantumdeeltjes twee mogelijke antwoorden op deze vraag te zijn. Er zijn deeltjes die hun soortgenoten “uitsluiten”, en waarvan er zich in elke toestand dus hooguit één kan bevinden. Er zijn ook meer “sociale” deeltjes, waarvan er zich willekeurig veel in elke toestand kunnen bevinden. Dit verschil in statistiek blijkt de eigenschap te zijn die maakt dat wij een deeltje als een “materiedeeltje” of als een “krachtgolfje” ervaren.
De statistiek van de eerste soort deeltjes – deeltjes die elkaar uitsluiten – werd voor het eerst in detail beschreven door de Italiaanse natuurkundige Enrico Fermi en de Engelsman Paul Dirac. Hun statistiek wordt daarom ook wel Fermi-Diracstatistiek genoemd, en dergelijke deeltjes werden door Dirac later fermionen genoemd. Deze deeltjes kunnen niet in dezelfde toestand zijn – dus in het bijzonder: niet op dezelfde plaats. We ervaren ze daarom als “hard”: fermionen zijn een soort “legoblokjes” waaruit we dingen kunnen opbouwen. Dit is de reden dat we fermionen ervaren als materiedeeltjes.
De deeltjes die zich juist wel in dezelfde toestand kunnen bevinden, werden in detail beschreven door Albert Einstein en de Indiase natuurkundige Satyendra Nath Bose. Hun statistiek wordt daarom ook wel Bose-Einsteinstatistiek genoemd. Dirac gaf dergelijke deeltjes later de naam bosonen, als eerbetoon aan het werk van Bose. Bosonen kunnen zich in dezelfde toestand bevinden; ze kunnen dus ook moeiteloos door elkaar heen bewegen. Dit is de reden dat we deze deeltjes in de natuur ervaren als golven die een interactie kunnen overbrengen.
| Veld | Deeltje | Soort | Uitsluiting | Spin |
| Elektromagnetische veld | Foton | Boson | Nee | 1 |
| Elektronveld | Elektron | Fermion | Ja | 1/2 |
In de bovenstaande tabel hebben we onze eerdere twee voorbeelden in kolom 3 en 4 aangevuld met wat we nu weten. In de tabel staat nog een vijfde kolom: hier staat de spin van het deeltje vermeld. Het begrip spin kwamen we in het artikel over verstrengeling al tegen. We zagen daar dat een elektron op twee verschillende manieren kan rondtollen, die we “spin up” en “spin down” noemen. Het is ook gebruikelijk om die twee toestanden met de getalswaarden “+1/2” en “-1/2” aan te geven, en om de grootst mogelijke van die waarden, 1/2, kortweg de “spin van het elektron” te noemen. Op een soortgelijke manier blijkt een foton op drie manieren te kunnen “rondtollen” (die manieren worden ook wel polarisaties genoemd), en die drie manieren worden aangegeven met de getalswaarden -1, 0 en +1. Er wordt dan ook wel gezegd dat het foton “spin 1” heeft. Er zijn ook deeltjes die maar op 1 manier kunnen rondtollen (en dus spin 0 hebben), deeltjes die op 4 manieren kunnen rondtollen (en dus spin 1 1/2 hebben), enzovoort.
Als we nu de tabel hierboven zouden uitbreiden met alle soorten bekende deeltjes, zou direct iets opvallen. Alle bosonen die we in de natuur tegenkomen blijken heeltallige spin (dus 0, 1, 2, enzovoort) te hebben, terwijl alle fermionen halftallige spin (dus 1/2, 1 1/2, enzovoort) hebben. Er blijkt dus een rechtstreeks verband te zijn tussen de spin van een deeltje en zijn statistiek!
Het blijkt mogelijk te zijn om dit verrassende verband wiskundig te bewijzen. Helaas zou het veel te ver voeren om dat bewijs hier te geven. Het bewijs maakt gebruik van bepaalde symmetrie-eigenschappen die het onderscheid tussen deeltjes met heeltallige en halftallige spin bepalen. Aan de hand van die symmetrie-eigenschappen kan worden aangetoond dat de ene soort deeltjes zich wel in dezelfde toestand kan bevinden, zonder de symmetrie te verbreken, en de andere soort niet. De eerste die een dergelijk argument gaf was de Zwitser Markus Fierz in 1939; een uitgebreider bewijs werd vervolgens in 1940 gegeven door de Zwitsers-Oostenrijkse natuurkundige Wolfgang Pauli. Het feit dat deeltjes met halftallige spin elkaar uitsluiten, wordt nog altijd naar hem het uitsluitingsprincipe van Pauli genoemd.
Samenvattend zien we dat er in de natuur dus twee soorten deeltjes (oftewel golven, oftewel velden) zijn: fermionen, met halftallige spin, waaruit de materie om ons heen is opgebouwd, en bosonen, met heeltallige spin, die de krachten tussen de deeltjes overbrengen. Een logische volgende vraag is nu: hoeveel verschillende soorten bosonen en fermionen zijn er in de natuur? Ook op die vraag blijkt een heel overzichtelijk antwoord te bestaan. Dat antwoord leidt ons naar het standaardmodel van de elementaire deeltjes, dat we in het volgende artikel zullen bespreken.
Dit is het dertiende artikel uit het dossier Quantumfysica. In het veertiende artikel bespreken we het standaardmodel van de elementaire deeltjes.