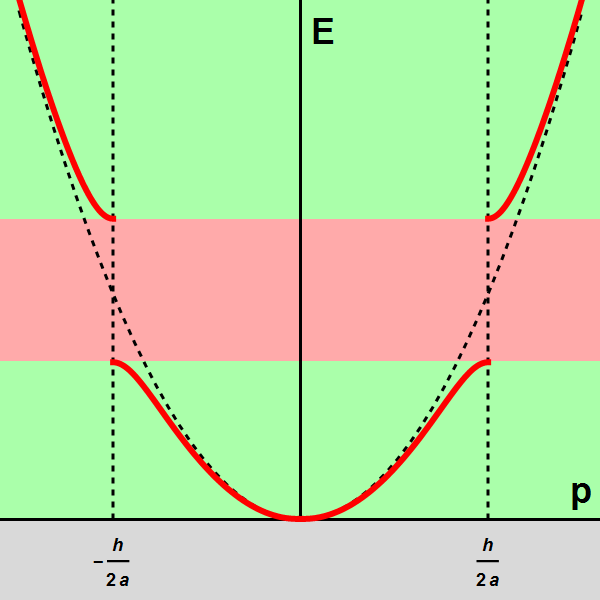
Afbeelding 1. Energiebanden.Als de impuls (snelheid maal massa) van een elektrongolf toeneemt, neemt ook de energie toe. Dat gebeurt echter niet op een continue manier (gestippelde parabool), maar bij bepaalde waarden van de impuls met sprongen. Het gevolg is dat bepaalde ‘banden’ van energiewaardes wél kunnen voorkomen, en andere niet.
Recap: energiebanden
In afbeelding 1 hierboven hebben we nog eens het diagram weergegeven waarmee het vorige artikel eindigde. In dat artikel bekeken we een heel eenvoudig model voor een metaal: een ééndimensionale rij van ionen, met onderlinge afstand a, waardoorheen elektrongolven onder invloed van de afstotende ionen bewegen.
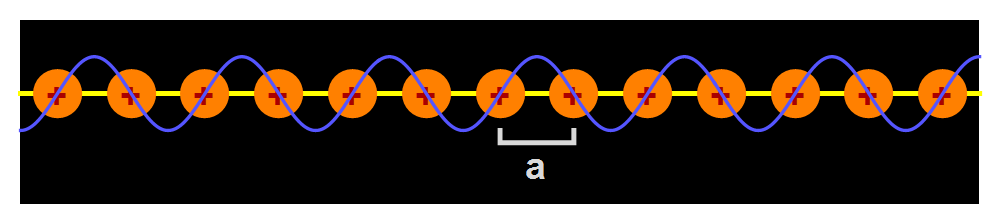
Afbeelding 2. Een eenvoudig model van een materiaal.In een ééndimensionaal ‘rooster’ van ionen kunnen elektrongolven bewegen. De elektronen zijn negatief geladen, en ondervinden dus een invloed van de positief geladen ionen.
We hebben gezien dat de energie E van de elektrongolf afhangt van zijn snelheid v – of preciezer: van de impuls p, die gedefinieerd is als de elektronmassa maal de snelheid: p = m v. De energie wordt, zoals te verwachten was, groter als de impuls en dus de snelheid groter worden, maar het cruciale resultaat van het vorige artikel is dat deze afhankelijkheid sprongen vertoont, zoals weergegeven in afbeelding 1. Er zijn dus ’toegestane’ en ‘verboden’ banden van energiewaardes.
Een belangrijk gevolg van het bestaan van deze energiebanden is het volgende. Voor impulsen die iets kleiner zijn dan de kritieke waarde
pc = h / 2a
is de energie beduidend minder groot dan voor impulsen die iets groter zijn dan pc. Met andere woorden: het kost heel veel energie om een elektron met een impuls net onder deze waarde iets meer snelheid te geven!
Een eenvoudige rekensom met grote gevolgen
Het blijkt zo te zijn dat de kritieke impuls pc niet zomaar een impulswaarde is, maar dat die in een heel bijzonder geval bereikt wordt. Dat kunnen we inzien door een betrekkelijk eenvoudige rekensom. Laten we aannemen dat ons eenvoudige, ééndimensionale stuk materiaal in totaal N ionen bevat, en laten we de lengte van het materiaal L noemen. De afstand a tussen twee ionen is dan dus gelijk aan
a = L / N
Een opmerking terzijde: de oplettende lezer merkt misschien op dat het aantal ion-afstanden tussen N ionen gelijk is aan N-1, zodat we dus eigenlijk a = L / (N-1) zouden moeten schrijven. In een realistisch materiaal is N echter een getal van acht of negen cijfers, zodat we het verschil tussen delen door N en delen door N-1 kunnen verwaarlozen.
In het vorige artikel hebben we gezien dat de kritieke impuls pc precies die is waarbij de halve golflengte van deelektrongolf gelijk is aan de afstand tussen twee ionen. Laten we deze kritieke golflengte λc noemen:
λc = 2 a
We kunnen in deze formule natuurlijk de vorige invulen, en vinden dan
λc = 2 L / N
Dit blijkt een heel speciale golflengte te zijn! Om dat te begrijpen, moeten we terugdenken aan het artikel over het Fermi-oppervlak. In dat artikel zagen we dat elektronen de neiging vertonen om zo lang mogelijke golflengtes te hebben: daarmee hebben ze immers de laagst mogelijke energie. Tegelijkertijd kunnen twee elektronen nooit in precies dezelfde toestand zijn. De langst mogelijke golflengte die een elektron in ons materiaal kan hebben, is bijvoorbeeld 2L – bij die golglengte past er precies één buik van de golf in het materiaal, zodat de golf op de twee randen netjes 0 is.
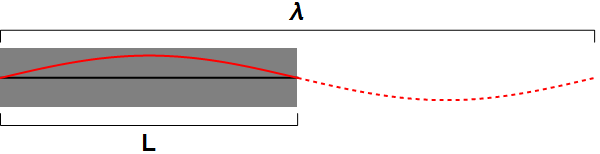
Afbeelding 3. De langste golflengte.De langste golmlengte die in een materiaal past, is tweemaal de lengte van het materiaal zelf: λ = 2 L. Op die manier past er precies één ‘buik’ van de golf in de lengte L van het materiaal.
Nu is het niet helemaal zo dat er dus maar één elektrongolf een golflengte van 2L kan hebben. Het elektron heeft namelijk ook nog een spin – grof gezegd: het kan ‘rechtsom’ of ‘linksom’ draaien. Die twee draaiingsrichtingen geven verschillende toestanden, en dus zijn er volgens het uitsluitingsprincipe van Pauli twéé elektronen die een golflengte van 2L kunnen hebben. De volgende twee elektronen hebben dan een golflengte van L (oftewel: 2L / 2), zodat er precies twee buiken van de golf in het materiaal passen. De twee elektronen daarna hebben een golflengte van 2L/3, zodat er drie buiken passen, enzovoort.
Zijn er nu in ons materiaal M verschillende elektronen, dan ‘vullen’ die de toestanden met de M/2 langste golflengtes. Dat getal moeten we als M oneven is natuurlijk naar boven afronden, maar ook die afronding is een minimale wijziging ten opzichte van het enorme getal M/2, dus we zullen dat in onze berekening achterwege laten. De kortste golflengte die voorkomt is dan dus
λmin = 2 L / (M/2) = 4 L / M
Als we deze uitdrukking vergelijken met de uitdrukking voor de kritieke golflengte λc hierboven, zien we dat die uitdrukkingen erg op elkaar lijken. Die gelijkenis wordt nog groter als we beseffen dat M en N niet geheel onafhankelijke getallen zijn. Ter herinnering: N is het aantal ionen in ons materiaal; M is het aantal elektronen. In de meeste materialen zal het zo zijn dat elk atoom een vast aantal elektronen afstaat, die vrij door het materiaal kunnen bewegen. Als dit er per atoom één is, zijn de aantallen ionen en elektronen dus precies gelijk: N = M. Staat elk atoom twee elektronen af, dan vinden we dat M = 2N, en dus vinden we in dat geval
λmin = λc
Kortom: in dit geval heeft het snelste elektron (dat met de kortste golflengte) exact de kritieke impuls pc! Het zal heel lastig zijn om dit elektron (of ieder ander elektron) iets meer snelheid te geven. Maar – zie afbeelding 4 hieronder, overgenomen uit ons artikel over het Fermi-oppervlak – dat laatste is precies wat we zouden moeten doen om een stroom door het materiaal te laten lopen! Kortom: we hebben een isolator gevonden: een materiaal waarin het heel moeilijk is om de elektronen extra sneleid te geven en zo elektrische stroom op te wekken.
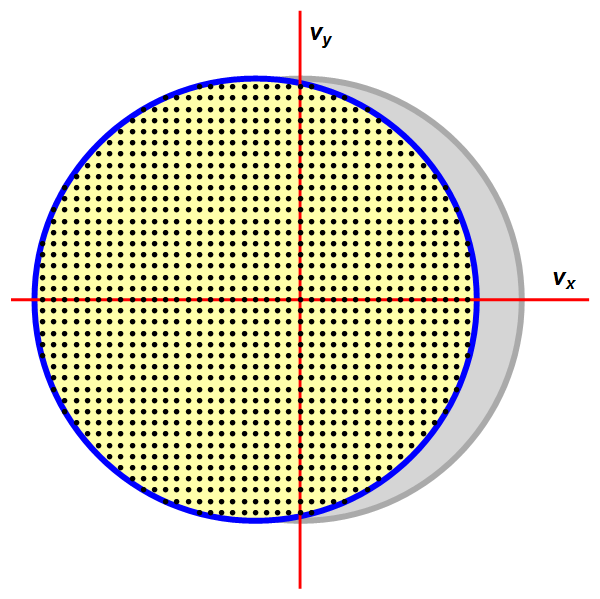
Afbeelding 4. Stroom en Fermi-oppervlak.Het blauwe Fermi-oppervlak (hier weergegeven voor een tweedimensionaal materiaal in plaats van ons ééndimensionale voorbeeldgeval) omvat alle elektronsnelheden die voorkomen als de elektronen in het materiaal de laagst mogelijke energieën hebben. In dit geval bewegen de elektronen alle kanten op, en loopt er dus geen netto stroom. Om een stroom te laten lopen moeten we alle elektronen dus een kleine extra snelheid geven (de grijze cirkel). Als bepaalde elektronen hiervoor een energeband moeten oversteken, kost dit erg veel energie: een isolator. Als de elektronen nog ‘ruimte’ in dezelfde energieband hebben kost het versnellen weinig energie: een geleider.
Hebben we een materiaal dat per atoom één elektron afstaat (M = N), dan is
λmin = 2 λc
en kost het dus geen enkele moeite om de snelste elektronen nog een iets kortere golflengte te geven (zolang die maar boven λc blijft) en om dus een elektrische stroom te laten lopen. Zo’n materiaal is dus een geleider!
Dit patroon blijkt zich te herhalen als er per atoom meer vrije elektronen zijn. Zijn er vier van zulke elektronen, dan wordt exact een volgende grens-golflengte bereikt, waarbij ook weer een energiesprong gemaakt moet worden naar de volgende energieband om de elektronen een extra snelheid te geven. Ook dan is het materiaal dus weer een isolator. Zijn er drie vrije elektronen per atoom, dan bevinden de snelste elektronen zich middenin zo’n band, en hoeven er geen sprongen gemaakt te worden – in dat geval hebben we dus weer een geleider.
Meer dimensies
In ons ééndimensionale model is het resultaat dus dat een materiaal stroom geleidt als er een oneven aantal geleidingselektronen is, en stroom tegenhoudt als er een even aantal geleidingselektronen is. Is dit resultaat ook geldig in driedimensionale materialen?
Grofweg is het antwoord op die vraag ‘ja’, maar er zijn allerlei details die het driedimensionale geval (of zelfs de tussenvorm in twee dimensies) wat gecompliceerder maken. We zullen deze verschillen niet in detail uitwerken – de wiskunde daarvoor zou te ingewikkeld worden voor dit inleidende artikel – maar we zetten ze kort op een rijtje.
- In één dimensie vinden de energiesprongen plaats bij specifieke waarden van de impuls p – zie afbeelding 1. In twee of drie dimensies is de impuls echter een vector (pijltje) met twee of drie componenten. Als de ionen in meer dimensies in een rechthoekig rooster zitten (zie afbeelding 5 bovenin voor een tweedimensionaal voorbeeld), vinden de energiesprongen nog steeds bij heel specifieke waarden plaats, maar nu bij specifieke waarden voor de individuele componenten van de impuls. De impuls in de x– óf in de y-richting moet in het tweedimensionale rechthoekige voorbeeld dus een bepaalde waarde overstijgen om een energiesprong te maken.
- Bevinden de ionen in meer dimensies zich in een ingewikkelder configuratie, dan worden de waardes van de impulsen waar zich een energiesprong voordoet ook ingewikkelder. In afbeelding 5 onderin zien we bijvoorbeeld ionen die in een tweedimensionaal driehoekig patroon zijn gerangschikt; het blijkt dat de impuls in dit geval bij het overschrijden van de rand van een zeshoek in de tweedimensionale ‘impulsruimte’ voor een energiesprong zorgt. Dit gebied in de impulsruimte wordt de Brillouin-zone genoemd. In drie dimensies wordt dit patroon van ion-configuraties en Brillouin-zones nog ingewikkelder.
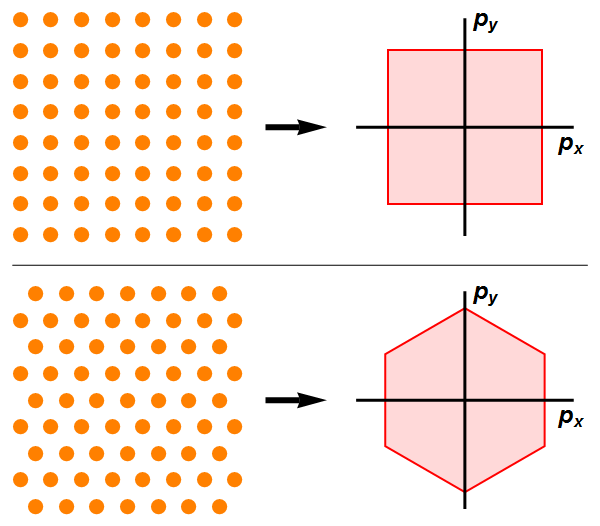
Afbeelding 5. Brillouin-zones.In een tweedimensionaal materiaal kunnen de ionen zich in een rechthoekig rooster bevinden (boven), maar bijvoorbeeld ook in een driehoekig rooster (onder). In het eerste geval vinden de energiesprongen plaats als de impuls de rode rand van het vierkant overschrijdt, dus als de x- óf de y-component van de impuls een bepaalde waarde passeert. In het tweede geval vinden de energiesprongen plaats als de impuls de rode rand van de zeshoek overschrijdt.
- Als de elektronen geen invloed van de ionen ondervinden, is het Fermi-oppervlak in twee dimensies een cirkel, zoals in afbeelding 4, en in drie dimensies een bol. Onder invloed van het patroon van de ionen worden deze oppervlakken echter vervormd. In afbeelding 6 hieronder zien we bijvoorbeeld het eindresultaat voor (driedimensionaal) koper: de lijnen geven de Brillouin-zone weer, en de gele vorm het Fermi-oppervlak. We zien dat het Fermi-oppervlak ruimschoots binnen de Brillouin-zone ligt, waardoor de meeste elektronen in het koper gemakkelijk hun snelheid kunnen veranderen. Koper is dan ook een geleider.
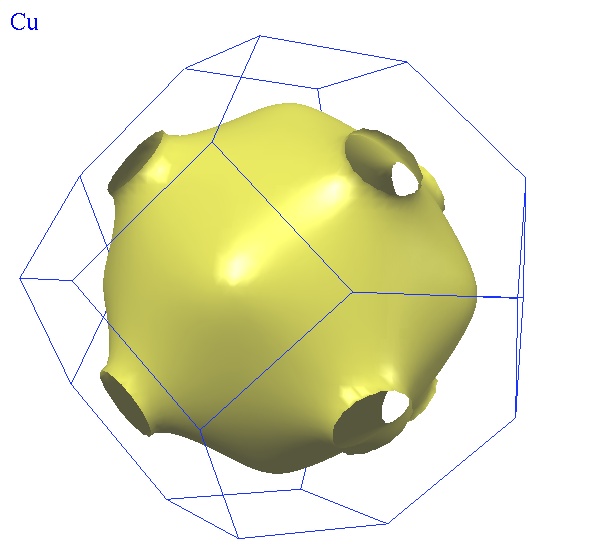
Afbeelding 6. De Brillouin-zone en het Fermi-oppervlak van koper.Het Fermi-oppervlak ligt ruimschoots binnen de Brillouin-zone, en de meeste elektronen kunnen dus gemakkelijk hun snelheid iets veranderen. Koper is daarom een geleider. Afbeelding: The Fermi Surface Database.
Ondanks deze belangrijke verschillen is het vaak zo dat de les uit ons ééndimensionale voorbeeld nog geldt. Heeft een materiaal een oneven aantal geleidingselektronen per atoom, dan is het een geleider; heeft het een even aantal geleidingselektronen per atoom, dan is het een isolator. Er zijn echter beslist uitzonderingen op deze regel. Soms wordt het Fermi-oppervlak van een materiaal met twee geleidingselektronen per atoom bijvoorbeeld zo sterk vervormd, dat een groot deel van het Fermi-oppervlak ‘uitpuilt’ buiten de Brioullin-zone. Veel elektronen hebben dan de energiesprong dus al gemaakt, en kunnen gemakkelijker versnellen. Zo kunnen materialen met een even aantal geleidingselektronen per atoom dus toch soms stroom geleiden.
Hiermee hebben we ons eerste doel in deze artikelenreeks bereikt: we begrijpen nu veel beter hoe het zit met het al dan niet geleiden van stroom door materialen. Maar hoe zit het met die bijzondere tussenproducten – de halfgeleiders? Daarover gaan we het in het vervolg van deze serie hebben.
Het volgende artikel in dit dossier verschijnt op vrijdag 23 april.