
Afbeelding 1. Een rooster van ionen.In onze bespreking van geleiding hebben we tot nu verwaarloosd dat de elektronen door een ‘achtergond’ van geladen ionen bewegen. In dit artikel zullen we zien dat deze ionen zorgen voor een bandenstructuur in de energieën die de elektronen kunnen hebben.
- De invloed van de ionen
- Lange golflengtes
- Korte golflengtes
- Eigentoestanden van energie
- Andere golflengtes
- De kleine lettertjes
- Energiebanden
De invloed van de ionen
Tot nu toe hebben we het materiaal waarin onze elektrongolven bewegen, gezien als een leeg ’toneel’ dat geen invloed heeft op de golven zelf. Dat is natuurlijk maar een heel grove benadering, zeker als we kijken naar de verdeling van lading in het materiaal. Elektronen zelf zijn negatief geladen, maar het materiaal als geheel zal normaalgesproken ongeladen zijn, en dus evenveel positief als negatief geladen deeltjes bevatten. Als er elektronen vrij door het metaal bewegen (meestal één of hooguit enkele elektronen per atoom) blijven er positief geladen ionen achter. In de meeste materialen vormen die ionen een vast en regelmatig rooster, zoals in afbeelding 1. Het ’toneel’ waarover de elektrongolven bewegen, is dus een regelmatig rooster van positieve ladingen. Dit blijkt cruciale gevolgen te hebben voor het geleiden van elektrische stroom.
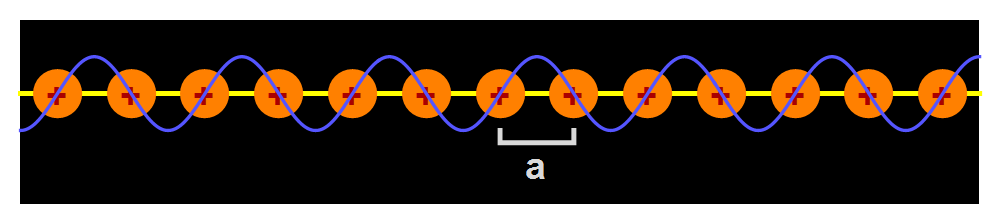
Om die gevolgen te kunnen begrijpen, zullen we in de rest van dit artikel kijken naar een eenvoudig ééndimensionaal model. Zie afbeelding 2: we hebben een regelmatige verdeling van positief geladen ionen (met onderlinge afstand a) op een lijn, waar de negatief geladen elektrongolven doorheen bewegen. De vraag is nu: hoeveel trekken de negatief geladen elektrongolven zich aan van het positief geladen ionenrooster?
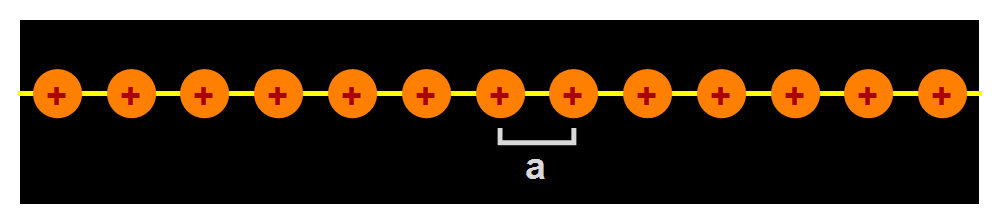
Afbeelding 2. Een ééndimensionaal ionenrooster.Voor het gemak bekijken we in de rest van dit artikel een materiaal met één dimensie. De elektrongolven bewegen van links naar rechts of van rechts naar links, en komen daarbij positief geladen ionen met een onderlinge afstand a tegen.
Lange golflengtes
Laten we om te beginnen de bovenstaande vraag, wat elektrongolven merken van het ionrooster, beantwoorden voor golven met een heel lange golflengte – veel langer dan de afstand a. Voor zulke golven is het antwoord namelijk eenvoudig: zij trekken zich nauwelijks iets aan van de geladen ionen. De golflengte van zulke golven is zo groot, dat zich binnen één golflente een enorm aantal ionen bevindt. De golf beweegt zich dus door een vrijwel homogeen geladen medium, en zal de ‘structuur’ van dat medium op schaal a nauwelijks ervaren. Vergelijk het met een glas water: dat bestaat uit losse watermoleculen, maar wij zijn als mensen zoveel groter dan die moleculen, dat we deze ‘korreligheid’ van water niet ervaren. Voor ons is water een gladde, continue substantie.
Voor heel lange elektrongolven is het ionenrooster ook een glad, coninu medium, en dus zullen deze golven door het metaal bewegen als over een leeg toneel. In het bijzonder zijn al onze resultaten uit het eerste artikel van deze serie voor zulke golven dus geldig:
- De quantumgolven kunnen allerlei vormen aannemen, maar de golven met één specifieke energie zijn vrijwel exact sinusvormig (of ‘vlak’ – zie afbeelding 3).
- Zulke vlakke golven hebben een bepaalde snelheid v, en een bijbehorende impuls p = m v die we kunnen uitrekenen door de snelheid v met de elektronmassa m te vermenigvuldigen.
- Zulke vlakke golven hebben een golflengte λ, die omgekeerd evenredig is met de snelheid (en de impuls), volgens de De Broglie-relatie p = h / λ. De constante h in deze relatie is de constante van Planck.
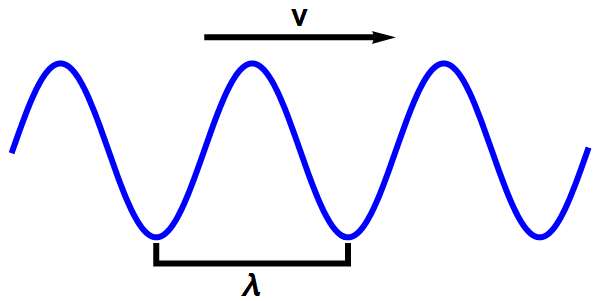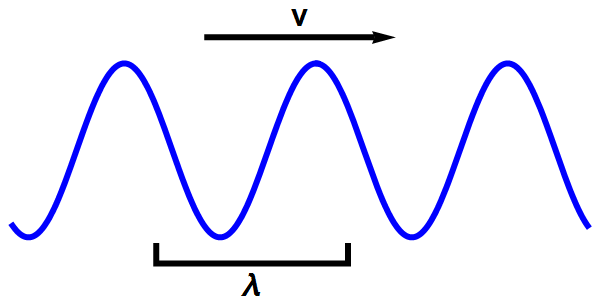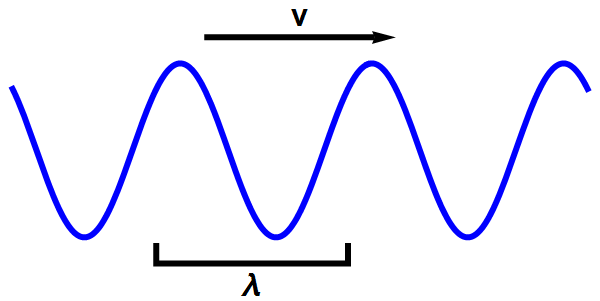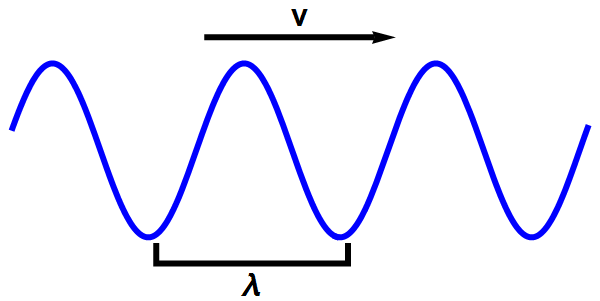
Afbeelding 3. Een vlakke golf.Een lopende sinusvormige golf die in één dimensie beweegt.
We kunnen ook eenvoudig de energie van zulke vlakke golven uitrekenen. Een beroemde formule uit de middelbareschoolnatuurkunde zegt dat bewegingsenergie (‘kinetische energie’) en snelheid voldoen aan het verband
E = ½ m v2
waarin m weer de massa van het elektron is. In plaats van de snelheid v kunnen we in deze formule ook de impuls p = m v gebruiken; de formule wordt dan
E = p2 / (2m)
Geen liefhebber van zoveel formules? Geen zorgen: het eindresultaat valt namelijk ook mooi weer te geven in een plaatje. Zie afbeelding 4, waar we dit verband tussen energie en impuls in een grafiek tekenen. Het belangrijke aan deze grafiek is het volgende: Als de impuls toeneemt, groeit de energie. Dat gebeurt op een continue manier: de energie maakt nergens een ‘sprong’.
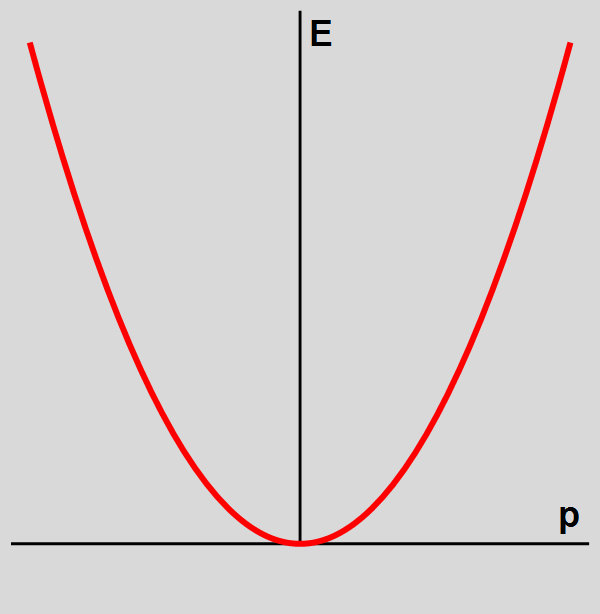
Afbeelding 4. Het verband tussen energie en impuls.Als de impuls toeneemt (en dus de snelheid toeneemt, en de golflengte afneemt), groeit de energie op een continue manier, zonder sprongen. Merk op dat negatieve impuls staat voor impuls en snelheid naar links, en positieve impuls voor impuls en snelheid naar rechts.
Korte golflengtes
Voor elektrongolven met korte golflengtes (en dus: hoge snelheden) verandert het bovenstaande verhaal drastisch. Zodra de golflengte λ van de elektrongolf vergelijkbaar wordt met de afstand a tussen de ionen in het materiaal, gaat de aanwezigheid van de ladingen de elektrongolf sterk beïnvloeden. Dit merken we het sterkst wanneer de halve golflengte van de elektrongolf precies gelijk is aan de afstand a tussen de ionen. Waarom de halve golflengte? Zie afbeelding 5: in één golfbeweging begint een golf op hoogte 0, gaat naar een piek, dan weer naar 0, dan naar een dal en weer naar 0. Een halve golflengte is dus de afstand tussen twee nulpunten, of tussen een piek en het volgende dal, en juist die afstand zal hieronder een belangrijke rol gaan spelen.
Afbeelding 5. Een bijzondere golflengte.Als de halve golflengte van de elektrongolf (hier weergegeven in het blauw) precies gelijk is aan de afstand a tussen twee ionen, blijkt er iets bijzonders te gebeuren met de golf.
Om te begrijpen wat er bij deze bijzondere golflengte gebeurt, moeten we ons een belangrijke eigenschap van quantummechanische golven herinneren. Zulke golven hebben namelijk zelden een exacte waarde voor een bepaalde ‘klassieke’ fysische grootheid. Voor de grootheid ‘plaats’ is dat het duidelijkst: een golf als in afbeelding 5 is nooit op één plaats, maar ‘een beetje hier, en een beetje daar’.
Iets soortgelijks geldt voor het begrip energie. Een willekeurige golf zal zelden één specifieke energie hebben, maar bestaan uit allerlei componenten met verschillene energieën. Wat dat betreft is het voorbeeld uit afbeelding 2, van de lopende vlakke golf met lange golflengte, heel bijzonder. Die golf heeft, omdat die de ionen (vrijwel) niet ‘ziet’, een (vrijwel) precies bepaalde snelheid, en een (vrijwel) precies bepaalde energie.
Dat laatste is niet meer het geval als de vlakke golf een korte golflengte heeft, en de ionen dus wel ‘ziet’. De golf zal dan interactie hebben met de ionen. De energie wordt daarbij mede bepaald door de aantrekking tussen de negatief geladen elektrongolf en de positief geladen ionen. Delen van de negatief geladen golf die dichtbij de positief geladen ionen zijn, zullen door de aantrekkingskracht voor een lagere energie zorgen dan delen die verder van de ionen af liggen. Dit alles zorgt ervoor dat een lopende golf zoals in afbeelding 2 geen exact bepaalde energie meer heeft.
Eigentoestanden van energie
Betekent dat, dat het überhaupt niet meer mogelijk is om een golf te maken die een heel precies bepaalde energie heeft? Verrassend genoeg blijkt dat met een slimme truc toch te kunnen. Een dergelijke golf, met een precies bepaalde energie, heet in vaktermen overigens een ‘eigentoestand van de energie’.
De truc blijkt te zijn om naast de elektrongolf met impuls p ook een golf met impuls -p door het materiaal te laten lopen – dus exact dezelfde golf, maar in tegengestelde richting. Zodra we dat doen gebeurt er iets bijzonders: de twee golven ’tellen op’ tot een staande golf: een golf die niet meer naar links of naar rechts beweegt, maar die lijkt ‘stil te staan’.
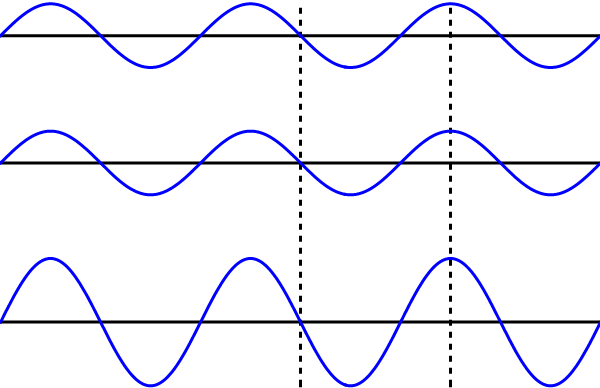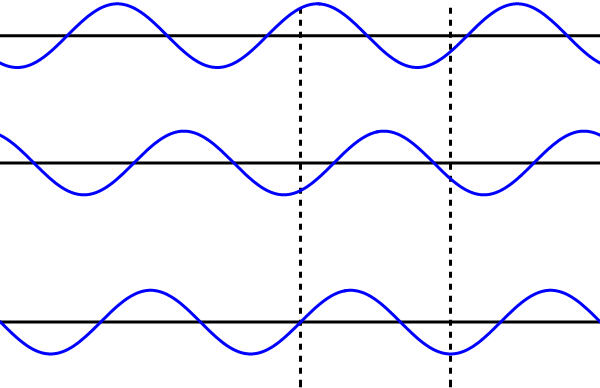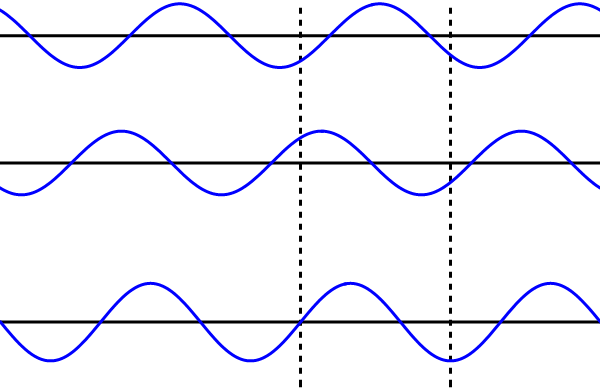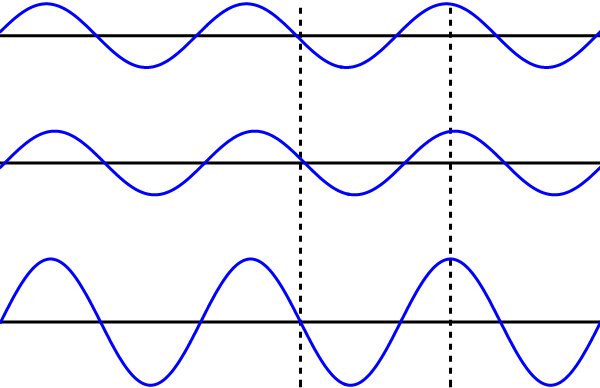
Afbeelding 6. Lopende en staande golven.Boven zien we een rechtslopende golf; daaronder precies dezelfde linkslopende golf. Als we deze twee golven tegelijk door een materiaal laten lopen, krijgen we verrassenderwijs een staande golf, zoals in het onderste plaatje. Bij de stippellijn in het midden zien we bijvoorbeeld dat de twee lopende golven elkaar steeds precies uitdoven; bij de stippellijn rechts versterken de golven elkaar als ze een piek of een dal hebben, en doven ze uit als ze beide 0 zijn.
Voor het geval waarin de halve golfengte van de lopende golven de ionafstand a is, blijkt uit de wiskunde achter de quantummechanica dat het deze staande golven zijn die een exact bepaalde energie hebben. Het bijzondere is daarbij dat de quantumregels twee van dit soort staande golven toelaten: één waarbij de pieken van de golven precies op de plaats van de ionen zijn, en één waarbij de pieken van die golven precies midden tussen de ionen in liggen – zie afbeelding 7.
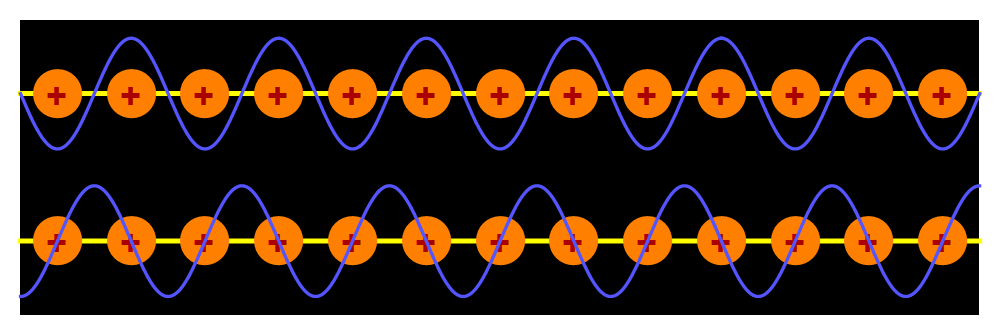
Afbeelding 7. Twee staande golven.De twee mogelijke golven met welbepaalde energie, in het geval waar de halve golflengte precies de ionafstand is. Beide golven zijn staande golven, net als de onderste golf in de animatie van afbeelding 6. In het bovenste geval bevinden de pieken van de negatief geladen golf zich in de buurt van de positief geladen ionen; de aantrekkende kracht tussen de ladingen zorgt dat deze oplossing een lage energie heeft. In het onderste geval bevinden de pieken zicht juist ver van de ionen; er is energie nodig om deze negatief geladen pieken van de positief geladen ionen te scheiden, en dus heeft deze oplossing een grotere energie.
Deze twee golven hebben beide een precies bepaalde energie, maar ze hebben beslist niet dezelfde energie! De negatief geladen elektrongolf wordt aangetrokken door de positief geladen ionen, en dus kost het beduidend minder energie om de golf te maken waarbij de pieken en dalen zich in de buurt van de ionen bevinden, dan het kost om de golf te maken waarbij de pieken en dalen zich ver van de ionen af bevinden. We ontdekken hier dus een bijzonder verschijnsel: we begonnen met een lopende golf die een vaste impuls p had, maar als we uit deze golf een golf willen construeren met een vaste energie E, moeten we ook de golf met impuls -p gebruiken, en vinden we twéé oplossingen, met een sprong in de energie tussen die twee oplossingen!
Andere golflengtes
De eenvoudige grafiek die we in afbeelding 4 tekenden, klopt voor dit geval dus beslist niet meer. Als we in de buurt van impuls 0 (extreem lange golflengte) beginnen, en de impuls steeds groter maken (dus de golflengte steeds korter), komen we op een gegeven moment bij de golflengte 2a uit, waar de helft van de golflengte gelijk is aan de afstand tussen de ionen. Hier zullen we zoals hierboven uitgelegd twee oplossingen voor de energie vinden, en niet één. We kunnen met de De Broglie-relatie ook de bijbehorende impuls uitrekenen waar dit gebeurt: die is dan gelijk aan
p = h / λ = h / (2a)
Aan de andere kant verwachten we in de buurt van p=0 (lange golflengtes) dat de elektrongolven de ionen niet ‘zien’, en dat de grafiek uit afbeelding 4 bij heel goede benadering klopt. De grote vraag is dus: wat gebeurt er tussen het gebied rond p=0 (lange golflengtes) en het gebied rond p = h / (2a) (halve golflengte gelijk aan de ion-afstand)?
Het exacte antwoord vergt helaas te veel wiskunde om hier uiteen te zetten, dus we zullen de oplossing zonder verdere berekeningen geven. Als we beginnen met een halve golflengte die iets langer is dan de ion-afstand a, vinden we als energie-eigentoestand een bijna-staande golf die erg lijkt op de bovenste golf (met lage energie) uit afbeelding 7. Als we beginnen met een halve golflengte die iets korter is dan de ion-afstand a, vinden we als energie-eigentoestand een bijna-staande golf die erg lijkt op de onderste golf (met hoge energie) uit afbeelding 7.
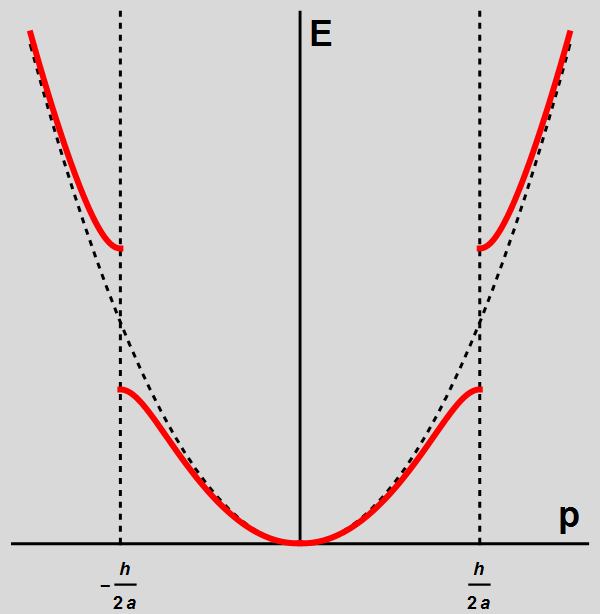
Afbeelding 8. Sprongen in de energie.De gestippelde parabool is het resultaat uit afbeelding 4, waarin we geen rekening hielden met het ionenrooster. Als we wél rekening houden met dit rooster (rode lijn) zien we dat de energie E gestaag toeneemt als we de impuls p steeds groter maken (en dus de golflengte steeds kleiner), maar dat er bij een bepaalde waarde van p een abrupte sprong in de energie optreedt.
Het volledige plaatje wordt daarmee zoals in afbeelding 8. We tekenen hier de relatie tussen impuls en energie, net als in afbeelding 4, maar nu met alle bovenstaande effecten meegenomen. In de buurt van p = 0, dus voor lange golflengtes, zien we dat de situatie vrijwel hetzelfde is als in het geval waarin we ons geen zorgen maakten over de geladen ionen. Zodra de halve golflengte precies ‘past’ op het ionrooster, bij impuls p = h / (2a) (en natuurlijk ook voor dezelfde negatieve waarde, waar we beginnen met een golf die naar links beweegt) zien we dat twee waarden voor de energie mogelijk zijn, met een sprong daartussen. Voor iets kleinere impulsen (langere golflengtes) is de energie continu verbonden met de laagste van die twee energiewaardes; voor iets grotere impulsen (kortere golflengtes) is de energie continu verbonden met de hoogste van de twee energiewaardes. De energie maakt dus, als we de golflengtes korter en korter maken op een gegeven moment een sprong!
De kleine lettertjes
De onderstaande paragraaf kan bij eerste lezing van dit artikel beslist overgeslagen worden: wat we hier vertellen is niet nodig om de rest van ons verhaal te begrijpen. De oplettende lezer vraagt zich echter misschien af: waarom kunnen we niet de bovenste golf uit afbeelding 7 nemen, en vervolgens de golflengte iets korter maken? Vinden we dan niet ook een tweede oplossing met iets grotere impuls dan p = h / (2a) maar met een lage energie? Waarom zou bij grotere impuls alleen de oplossing met hoge energie bestaan?
Het wat ingewikkelde antwoord op deze vraag is als volgt. Om van de golf met impuls p = h / (2a) een golf met specifieke energie te maken, moesten we daarbij een golf met tegengestelde impuls, p = -h / (2a) optellen. Beide golven zijn even sterk, en het resultaat is een staande golf, die in zekere zin ‘geen impuls meer heeft’. Bovendien vonden we in dit geval twee oplossingen met deze eigenschappen.
Als we nu beginnen met een golf met een impuls die iets groter is dan p = h / (2a), laten we zeggen met
p = h / (2a) + δ
voor een heel kleine waarde van δ, vinden we als we de wiskunde doen wederom twéé oplossingen die een exacte energie hebben. Voor beide oplossingen moeten we bij de oorspronkelijke golf de golf optellen met impuls
p = -h / (2a) + δ
Deze golf beweegt in de tegengestelde richting, en heeft een impuls die (in absolute waarde) iets kleiner is dan de golf waarmee we beginnen – zie afbeelding 9. Er is echter een belangrijk verschil tussen de twee oplossingen die we vinden. In de twee oplossingen voor p = h / (2a) telden we de twee lopende golven op met exact dezelfde sterkte – oftewel: dezelfde amplitude. In het geval dat de begin-impuls iets groter is, tellen we voor de ene oplossing de golf met negatieve impuls op met een iets kleinere amplitude, en in het andere geval met een iets grotere amplitude. In dit laatste geval is het echter wat vreemd om nog te spreken van een golf met positieve impuls: we tellen immers een golf met negatieve impuls erbij op, die een groter gewicht heeft, We kunnen deze tweede oplossing dus beter zien als een oplossing met negatieve impuls
p = -h / (2a) + δ
en niet als een oplossing met positieve impuls
p = h / (2a) + δ
Sterker nog: de tweede oplossing die we vinden is exact de oplossing die we gevonden zouden hebben als we met een golf met bovenstaande negatieve impuls zouden zijn begonnen. Ook deze oplossing bestaat dus wel degelijk, en is ook in de grafiek in afbeelding 8 verwerkt, maar die is daar te vinden bij impuls p = -h / (2a) + δ.
Energiebanden
Na deze kleine zijsprong voor de liefhebbers, gaan we terug naar de hoofdlijn van ons verhaal. We hebben gezien dat we de golflengtes van onze elektrongolven korter en korter kunnen maken, en dat de energie van deze golven daarbij geleidelijk toeneemt, tot we een golflengte bereiken waarbij de halve golflengte precies op het ion-rooster past. Daar maakt de energie opeens een sprong, en vervolgens neemt de energie, als we de golflengte nog korter maken, weer geleidelijk toe.
Dit verschijnsel blijkt zich te herhalen als de halve golflengte precies tweemaal op het ionrooster past, en nogmaals als de halve golflengte precies driemaal op het ionrooster past, enzovoort. Steeds maakt de energie een sprong, en wordt een bepaald energiebereik dus ‘overgeslagen’.
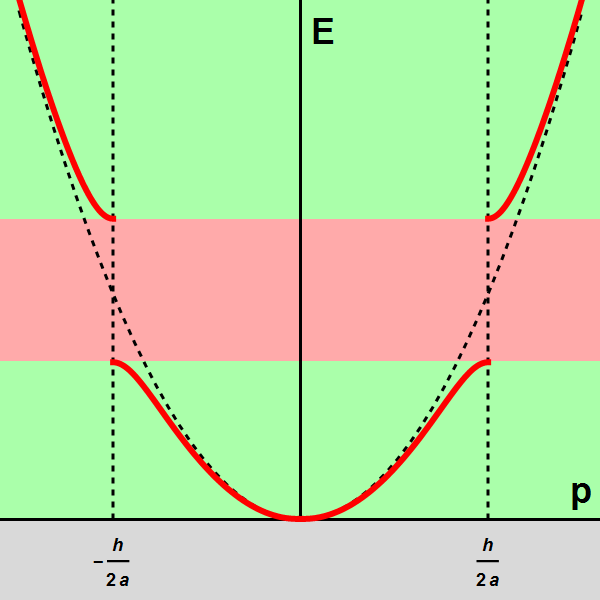
Afbeelding 9. Energiebanden.In een materiaal zijn, door het ionenrooster, bepaalde ‘banden’ van energie wel toegestaan voor de elektrongolven (groen), terwijl andere banden van energie niet voor kunnen komen (rood). Deze ’toegestane en uitgesloten energieën’ blijken uiteindelijk te bepalen of een materiaal een geleider of een isolator is.
Dit leidt uiteindelijk tot een patroon van energiebanden zoals weergegeven in afbeelding 9. De ’toegestane’ waardes van de energie voor elektrongolven bevinden zich in bepaalde banden (groen), waartussen zich ‘gaten’ bevinden van energieën die niet zijn toegestaan (rood).
Het blijkt deze bandenstructuur te zijn, die uiteindelijk bepaalt of een materiaal een geleider of een isolator is – of het dus elektrische stroom kan doorlaten, of niet. Hoe dat precies werkt, leggen we uit in het volgende artikel in deze serie.
Het volgende artikel in dit dossier verschijnt op vrijdag 8 april.