
Afbeelding 1. Het Fermi-oppervlak van zilver.Het Fermi-oppervlak bepaalt hoe de snelste elektronen in een bepaald materiaal bewegen. Hieronder zullen we zien dat Fermi-oppervlakken grofweg bolvormig zijn; waarom ze dat in de praktijk niet exact zijn zien we in het volgende artikel. Afbeelding: Alberto Marmodoro.
Het voorafgaande
Laten we beginnen met een heel korte opsomming van wat we in het eerste artikel in deze serie gezien hebben:
- Elektronen in een materiaal moeten we niet zien als deeltjes, maar als golven.
- Golven kunnen allerlei vormen hebben, maar zijn altijd opgebouwd uit vlakke, sinusvormige golven zoals in afbeelding 2.
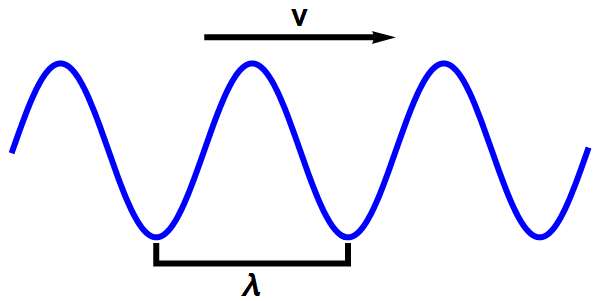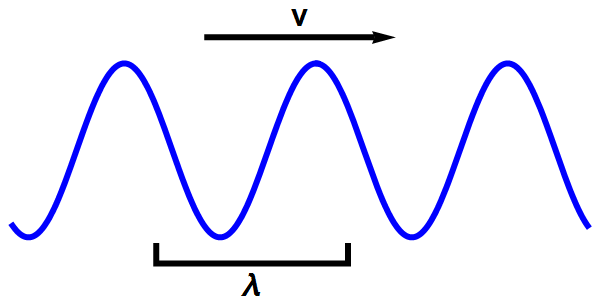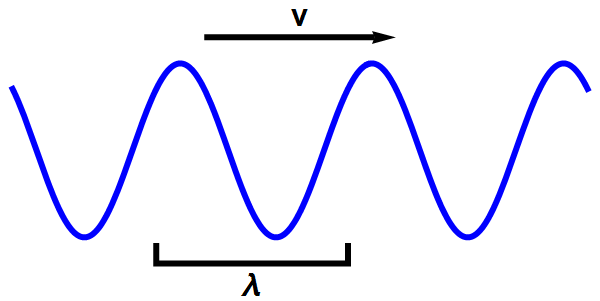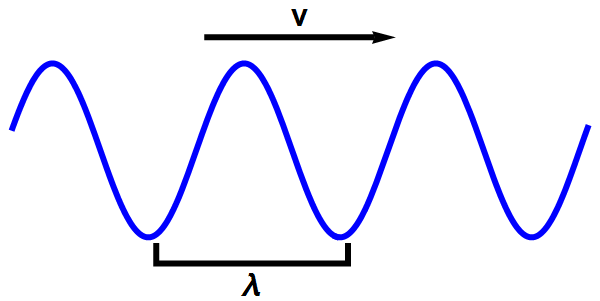
Afbeelding 2. Een vlakke golf in één dimensie.Een vlakke, sinusvormige golf heeft een golflengte λ en een snelheid v.
- Eigenschappen (plaats, snelheid, energie) van quantumgolven hebben in het algemeen niet één vaste waarde, maar een heel spectrum aan mogelijke waardes. Zo kan een quantumgolf, net als een watergolf, op allerlei plaatsen tegelijk zijn.
- Een bijzondere eigenschap van vlakke golven zoals in afbeelding 2 is dat ze wél een heel specifieke waarde voor snelheid en energie hebben. Die snelheid en energie hangen af van de golflengte van de golf: hoe groter de golflengte, hoe lager de snelheid en de energie.
- Een golf in een twee- of driedimensionaal materlaal kunnen we beschrijven met twee respectievelijk drie golflengte-componenten: één in elke richting van het materiaal. Samen bepalen deze componenten wat de totale golflengte, en dus de snelheid en energie van de golf is – zie afbeelding 3 voor een tweedimensionaal voorbeeld.
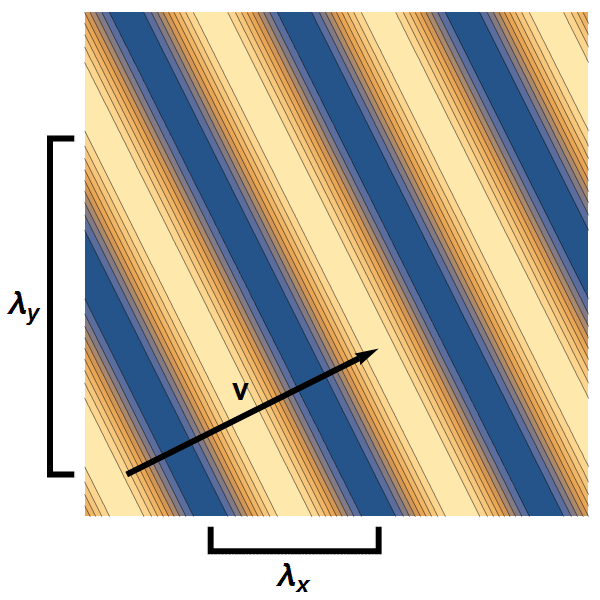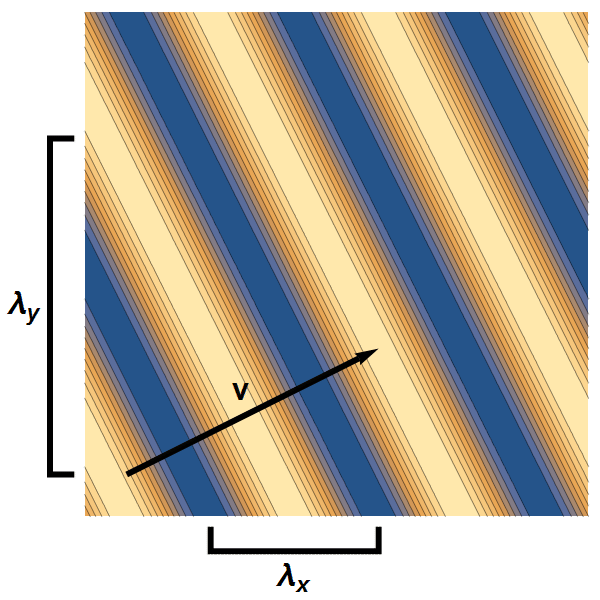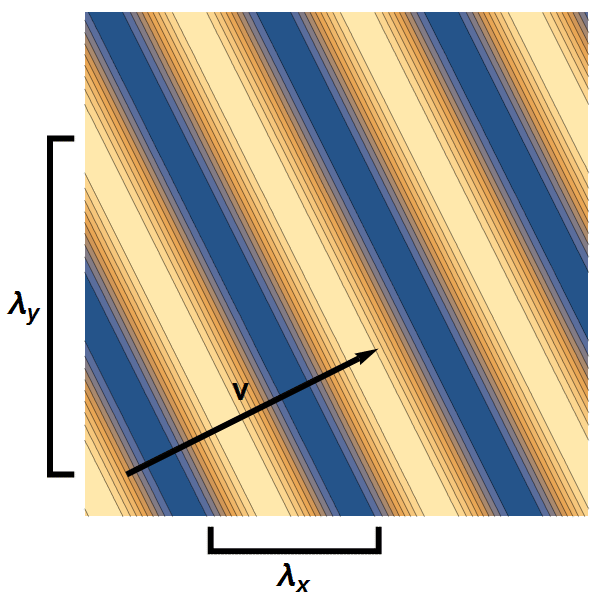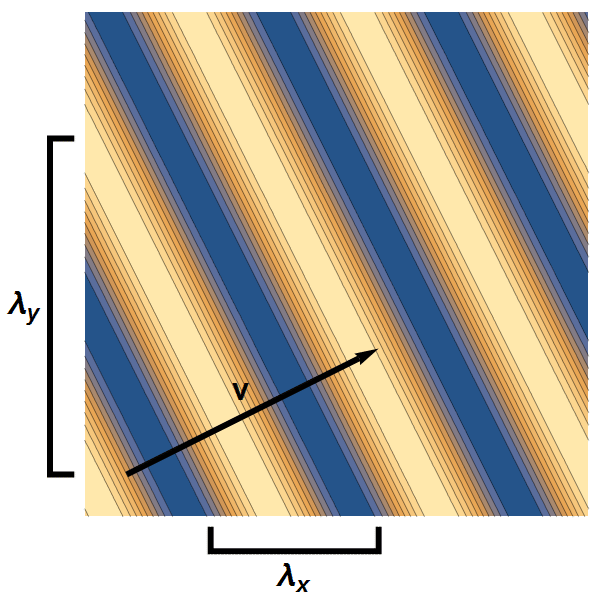
Afbeelding 3. Een vlakke golf in twee dimensies.Een tweedimensionale vlakke golf heeft twee golflenge-componenten. De snelheid heeft ook twee componenten, en heeft daarmee een grootte én een richting.
Het uitsluitingsprincipe van Pauli
De natuur heeft de neiging om energie zo gelijk mogelijk over de componenten van een systeem te verdelen. Een gevolg daarvan is dat systemen met veel energie die energie uiteindelijk aan hun omgeving zullen afstaan: een kop koffie koelt af; een rotsblok dat bovenop een berg ligt valt uiteindelijk omlaag en geeft zijn potentiële energie in de vorm van warmte af aan de omgeving. Met andere woorden: systemen zoeken uiteindelijk de toestand van de laagst mogelijke energie op.
We zouden verwachten dat dit ook geldt voor de elektronen in een stroomgeleidend materiaal: als we geen invloed op zo’n materiaal uitoefenen, zou het voor de hand liggen dat al die elektrongolven de toestand met de laagste energie opzoeken. Zoals we hierboven hebben gezien, is dat de toestand van een vlakke golf met de langst mogelijke golflengte-componenten. Met andere woorden: we zouden verwachten dat alle elektrongolven zich over het hele materiaal uitspreiden. De golflengtecomponenten worden daarmee zo groot mogelijk, de snelheidscomponenten dus zo klein mogelijk, en de energie ook zo klein mogelijk.
Er is echter een ander, typisch quantummechanisch principe dat hierbij roet in het eten gooit. Elektronen zijn namelijk fermionen: deeltjes waarvan er nooit twee in exact dezelfde toestand kunnen zijn. Dat er zulke deeltjes zijn, is een bijzonder gevolg van de quantummechanica, en is essentieel voor ons bestaan. Twee fermionen kunnen bijvoorbeeld nooit op exact dezelfde plaats zijn (in tegenstelling tot bosonen zoals lichtdeeltjes, die dwars door elkaar heen kunnen bewegen) – iets wat bijdraagt aan het feit dat fermionen als een soort ‘legoblokjes’ materie kunnen opbouwen. Veel meer over fermionen en bosonen valt te lezen in dit artikel uit ons dossier over quantummechanica.

Afbeelding 4. Wolfgang Pauli (1900-1958).De Oostenrijks-Zwitsers-Amerikaanse natuurkundige Wolfgang Pauli was één van de grondleggers van de quantummechanica. Het uitsluitingsprincipe is naar hem vernoemd.
Het feit dat twee elektronen nooit in exact dezelfde toestand kunnen zijn wordt het uitsluitingsprincipe van Pauli genoemd, naar de ontdekker ervan, de fysicus Wolfgang Pauli. Dit uitsluitingsprincipe betekent in het bijzonder dat niet alle elektronen in een materaal in de vlakke-golftoestand met de laagst mogelijke energie (en langst mogelijke golflengte) kunnen zijn. Iets preciezer: er kunnen maar twee elektronen in deze laagste energietoestand zijn. Waarom twee, en niet één? Omdat elektronen nog een extra eigenschap hebben: een soort ‘interne draaiing’, die we spin noemen. Die draaiing kan linksom en rechtsom zijn, en dus zijn er ook twee toestanden met de laagst mogelijke energie: eentje met spin linksom, en eentje met spin rechtsom.
De twee ‘langste elektrongolven’ zijn in alle richtingen over het hele materiaal verspreid en bewegen dus niet, maar de volgende elektronen moeten een kortere golflengte hebben, en dus een (kleine) snelheid in één van de richtingen van het materiaal. In een kubusvormig blokje materiaal kunnen we zo bijvoorbeeld golven maken die in twee van de richtingen precies de grootte van het blokje als golflengte-component hebben, maar in de derde richting twee golflengtes in de lengte van het materiaal bevatten. Er zijn drie mogelijke keuzes voor die richting, en de elektrongolven hebben daarmee ook een kleine snelheid in die richting – die natuurlijk ook nog eens twee kanten op kan staan. Bovendien kan elk van die toestanden voorkomen met spin linksom of rechtsom, dus in totaal leidt dit tot 3 x 2 x 2 = 12 vlakke elektrongolftoestanden met bijna de laagste energie. Een volgend elektron moet bijvoorbeeld in twee richtingen een iets kortere golflengte hebben (of in één richting en nóg kortere golflengte), en heeft daarmee dus nog iets meer energie, enzovoort.
Het Fermi-oppervlak
Uiteindelijk leidt de bovenstaande redenering tot het volgende plaatje. Elektronen zoeken een toestand op waarin hun snelheids-componenten zo klein mogelijk zijn (en hun golflengte-componenten dus zo groot mogelijk), en elk van die toestanden zal precies twee elektronen kunnen herbergen. In afbeelding 5 zien we het resultaat getekend voor een tweedimensionaal materiaal: elke stip staat hier voor een tweetal elektronen met bepaalde snelheidscomponenten, en het feit dat de elektronen hun snelheid zo laag mogelijk willen houden heeft tot gevolg dat alle elektronen zich in deze snelheidsweergave binnen een bepaalde cirkel rond snelheid 0 bevinden.
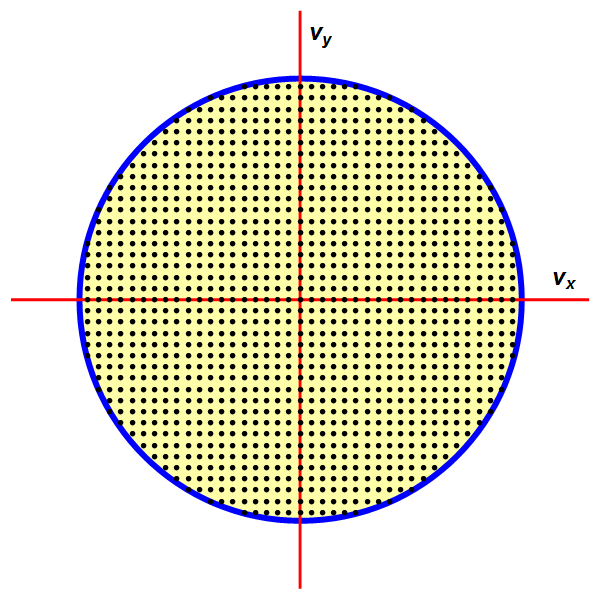
Afbeelding 5. Het Fermi-oppervlak van een tweedimensionaal materiaal.Op de assen staan de snelheden van de elektrongolven in de x– en y-richtingen aangegeven. De toestand met de laagste energie is degene waarin allebei deze snelheden nul zijn: het midden van de cirkel. Voor de andere toestanden geldt: hoe dichter bij het middelpunt, hoe lager de energie. Elke stip komt overeen met twee toestanden: één met spin rechtsom, één met spin linksom. De blauwe cirkel is het Fermi-oppervlak; die geeft aan wat de maximale snelheid van de elektronen tenminste moet zijn. In de parktijk gaat het hierbij om snelheden van honderden of zelfs duizenden kilometers per seconde.
Nu heeft een materiaal al snel een gigantisch aantal atomen – meestal een getal dat meer dan 20 cijfers bevat. Elk van die atomen heeft één of meerdere elektronen die voor stroomgeleiding zouden kunnen zorgen, en dus zullen de toestanden met heel lage energie al heel snel bezet zijn, en worden veel elektronen, zelfs als ze hun energie zo laag mogelijk willen maken, toch gedwongen om met forse snelheden door het materiaal te bewegen. De snelste elektronen in afbeelding 5 bevinden zich op de rand van de cirkel (of in een driedimensionaal materiaal op het oppervlak van een bol); deze rand wordt het Fermi-oppervlak genoemd. Het Fermi-oppervlak bestaat dus uit de elektrontoestenden die, van alle toestanden met zo laag mogelijke energieën, de hoogste energie hebben.
Hoe snel bewegen de elektronen die zich in de toestanden van het Fermi-oppervlak bevinden? Dat hangt van allerlei eigenschappen van het materiaal af, maar in het algemeen enorm snel: een typische snelheid van zulke elektronen is in de orde van honderden of duizenden kilometers per seconde! We zien hier het enorme effect dat de quantummechanica heeft op de eigenschappen van materialen: waar we ‘klassiek’ zouden verwachten dat alle elektronen in een materiaal bijna niet zouden bewegen, worden de elektronen door de quantummechanica gedwongen om met enorme snelheden door het materiaal te zoeven.
Geleiding
Het moge duidelijk zijn dat dit alles stroomgeleiding een stuk eenvoudiger maakt. Voor de stroomsterktes die we in het dagelijks leven tegenkomen, is het voldoende als de lading van de elektronen zich met een netto-snelheid van enkele millimeters per seconde door het materiaal beweegt. De snelheden van de elektrongolven hoeven daarvoor dus maar een heel klein beetje aangepast te worden.
Stel dat we bijvoorbeeld een spanningsbron op een metalen draad aansluiten. De spanningsbron zorgt voor een elektrisch veld in het materiaal, wat tot gevolg heeft dat de elektrongolven een neiging hebben om ’tegen het veld in’ te bewegen. (Niet ‘ met het veld mee’, omdat elektronen een negatieve elektrische lading hebben.) De gemiddelde snelheid van de elektronen – en daarmee het gehele fermi-oppervlak – zal dan dus iets verschuiven, tegen de richting van het elektrische veld in. We zien dit proces dat sterk overdreven getekend is in afbeelding 6.
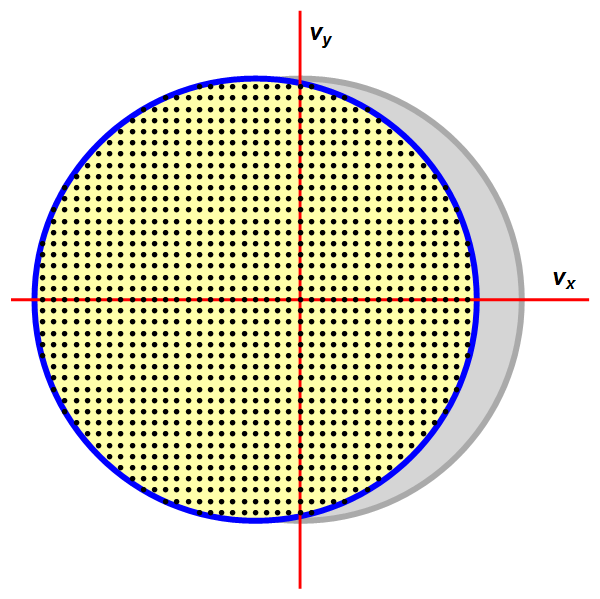
Afbeelding 6. Een verschoven Fermi-oppervlak.Een sterk overdreven weergave van wat er gebeurt als een materiaal stroom geleidt. De elektrongolven krijgen een snelheid die gemiddeld iets verschoven is ten opzichte van de ‘rustsituatie’. De grijze cirkel geeft het oorspronkelijke Fermi-oppervlak weer; de geel-blauwe cirkel het Fermi-oppervlak als er een stroom loopt. (In dit geval bewegen de elektronen gemiddeld naar links in de x-richting, als gevolg van een elektrisch veld naar rechts.) Het effect is hier sterk overdreven weergegeven: de gemiddelde snelheid van vele kilometers per seconde hoeft maar met een paar millimeter per seconde te veranderen om al een flinke elektrische stroom te creëren.
We zijn daarmee uitgekomen bij de quantummechanische beschrijving van elektrische stroom: stroom is niets anders dan een (minimale) verschuiving van het Fermi-oppervlak van de elektronen in het materiaal.
Die beschrijving is interessant, maar we begrijpen daarmee nog steeds niet waarom sommige materialen zo’n verschuiving wél toestaan, en andere níet! Om dat te kunnen begrijpen, moeten we een volgend quantumconcept invoeren: dat van energiebanden. Dat is dan ook het onderwerp van het volgende artikel in deze serie.
Dit is het tweede artikel uit het dossier ‘Quantumtoepassingen’. Het derde artikel zal verschijnen op vrijdag 25 maart.