Een voorbeeld: de harmonische oscillator
Een eenvoudig voorbeeld van een faseruimte is de faseruimte van een harmonische oscillator. Een harmonische oscillator is, in technische termen geformuleerd, een trillend systeem waarin de kracht evenredig is met de afstand tot een bepaalde evenwichtspositie.
Denk bijvoorbeeld aan een gewicht (of weer in nettere natuurkundige termen: een massa) die aan een veer hangt. Als we de massa voorzichtig ophangen, zal die in een bepaalde evenwichtstoestand blijven hangen. Als we de massa iets omlaag trekken, wordt de veer uitgerekt, en zal de veerkracht de massa omhoogtrekken. Hoe verder we de veer uitrekken, hoe groter de kracht wordt, en die twee grootheden zijn in goede benadering evenredig: als we de veer twee maal zo ver uitrekken, zal de veerkracht ook twee maal zo groot worden. Hetzelfde geldt als we de massa uit de evenwichtsstand omhoog duwen: de veer zal dan samengeduwd worden, en een kracht naar beneden uitoefenen. Ook deze kracht is evenredig met hoe ver we de massa omhoog duwen.
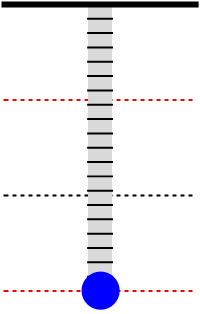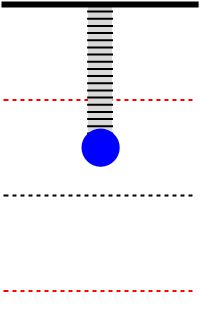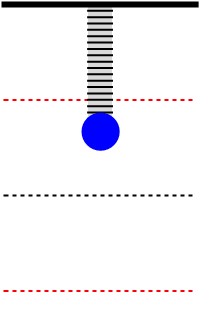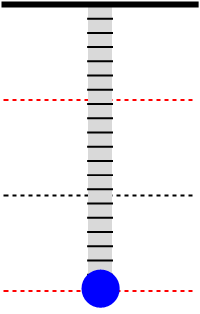
Afbeelding 1. Een harmonische oscillatorEen harmonische oscillator voert een regelmatige trilling uit. De zwarte stippellijn is de evenwichtstand.
Ook hier weer wat kleine lettertjes voor de oplettende lezer: in een realistische situatie zal natuurlijk ook de zwaartekracht op de massa werken. Waar we het hierboven over de veerkracht hebben, moeten we het dus eigenlijk hebben over de combinatie van de veerkracht en de zwaartekracht. Het blijkt dat voor die combinatie van krachten precies hetzelfde geldt als voor de veerkracht alleen, dus voor het gemak hebben we het in dit hoofdstuk alleen over de veerkracht. Wie het lastig vindt om de zwaartekracht “weg te denken”, kan zich voorstellen dat we het experiment niet op aarde uitvoeren, maar in een ruimteschip in een gewichtsloze toestand, waar geen zwaartekracht aanwezig is.
In afbeelding 1 zien we een animatie van de beweging van de massa aan de veer. De massa zal in een regelmatig patroon op en neer bewegen en steeds op hetzelfde hoogste en laagste punt van richting omkeren. Dat laatste is natuurlijk alleen waar in een ideale situatie, waar geen energie verloren gaat door wrijving met de lucht of door warmteontwikkeling in de veer. In een meer realistische situatie zal de massa langzaam energie verliezen en een steeds iets kleinere maximale uitwijking krijgen. Voor dit voorbeeld verwaarlozen we zulke effecten.
Hoe ziet de faseruimte van een harmonische oscillator eruit? Het voordeel van het simpele systeem dat we gekozen hebben, is dat de massa maar in één richting beweegt, zodat we de positie en de snelheid elk op een rechte lijn kunnen uitzetten. De totale faseruimte is dus tweedimensionaal, en valt op een stuk papier te tekenen. Zoals we in het hoofdstuk over configuratieruimtes al zagen, wordt het tekenen van een dergelijke ruimte voor een groter aantal componenten erg lastig. (Al kunnen we ook in dat geval prima met zo’n faseruimte rekenen.)
De harmonische oscillator heeft dus één positie-impulspaar. Hoe ver de uitwijking van de veer kan zijn, en hoe groot de snelheid van de massa kan worden, hangt af van allerlei eigenschappen van het systeem, zoals de lengte van de veer, de vraag wanneer de “rek” uit de veer is, enzovoort. In ons geïdealiseerde voorbeeld doen dergelijke eigenschappen er niet toe – we willen het voorbeeld zo eenvoudig mogelijk houden, dus we doen net alsof we de veer willekeurig ver kunnen uitrekken en indrukken, en of we de massa daarbij een willekeurige snelheid kunnen geven. Zolang we in de praktijk de uitwijking en snelheid van de massa niet te groot maken, zal dit geïdealiseerde model de werkelijkheid heel aardig benaderen. Als ons doel zou zijn om werkelijke veren te bestuderen, zouden we daarna natuurlijk allerlei correcties voor dergelijke materiaaleigenschappen in het model kunnen invoeren.
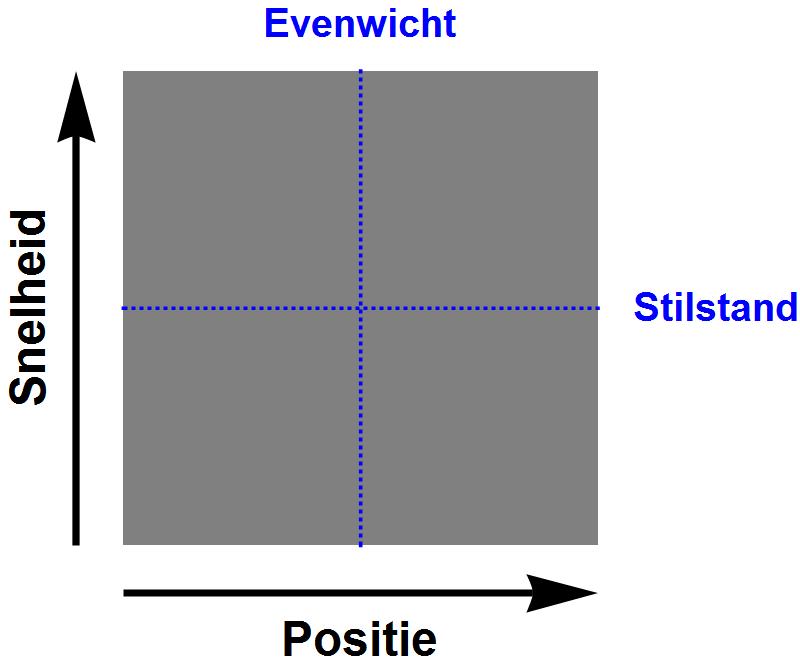
Afbeelding 2. De faseruimte van een harmonische oscillatorDe situaties waarin de snelheid nul is (“stilstand”) en waar de positie de evenwichtstoestand is, zijn in het blauw aangegeven. Let op: de terminologie is hier misschien wat verwarrend. De massa hoeft niet stil te staan in de evenwichtspositie; hij kan ook met een bepaalde snelheid door die positie heen bewegen. Hetzelfde geldt voor “stilstand”: de massa kan ergens anders (tijdelijk) tot stilstand komen dan in de evenwichtspositie: bijvoorbeeld op het moment dat de massa zijn hoogste punt bereikt en van richting omkeert.
De faseruimte is nu dus een plat vlak, waarin we in één richting de positie van de massa uitzetten, en in de andere richting de snelheid. Tot zover is deze faseruimte dus niet bijzonder interessant. Interessanter wordt het als we in de faseruimte ook de mogelijke bewegingen van de oscillator aangeven. Laten we daarvoor om te beginnen eens kijken naar de positie van de oscillator. In de animatie in afbeelding 3 zien we hoe die positie regelmatig (in een zogenaamde sinusgolf) heen-en-weerbeweegt tussen de twee maximale uitwijkingen.

Afbeelding 3. De positie van een harmonische oscillator
Vervolgens kijken we naar de snelheid van de massa. Als de uitwijking van de oscillator maximaal is, is de snelheid nul. Als de oscillator door de evenwichtsstand beweegt, is de snelheid het grootst – daarna remt de veer de massa immers weer af. We kunnen een soortgelijke animatie maken waarin we de snelheid van de oscillator uitzetten – zie afbeelding 4.

Afbeelding 4. De snelheid van een harmonische oscillatorDe snelheid is maximaal als de massa door de evenwichtsstand beweegt, en nul als de uitwijking maximaal is.
Tenslotte kunnen we zowel de positie als de snelheid van de massa weergeven als een beweging door de faseruimte. Een animatie hiervan is te zien in afbeelding 5. We zien dat de beweging van de massa in de faseruimte een cirkelvormige baan wordt, die de massa met constante snelheid doorloopt.
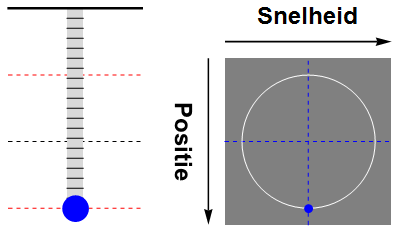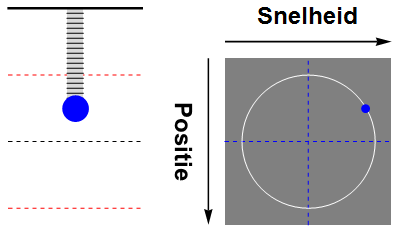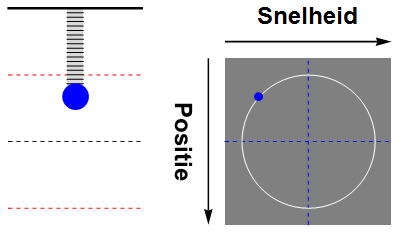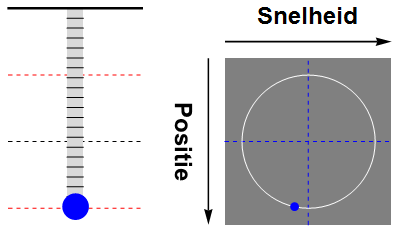
Afbeelding 5. Fasebaan van een harmonische oscillatorDe beweging van de harmonische oscillator als baan in de faseruimte. In de faseruimte is de baan een cirkel die met constante snelheid doorlopen wordt.
We hadden natuurlijk de massa een kleinere of juist een grotere beginuitwijking kunnen geven, met als gevolg dat ook de maximale snelheid kleiner of juist groter was geworden. De baan van het systeem in de faseruimte was dan nog altijd een cirkel geweest, maar met een grotere of kleinere straal. Uiteindelijk levert dat het volgende plaatje (afbeelding 6) op: de faseruimte is opgebouwd uit oneindig veel banen – in dit geval allemaal cirkels met verschillende stralen. Elk punt van de faseruimte ligt op precies één baan, en bepaalt die baan volledig. (We weten immers dat de positie en snelheid van de massa de hele toekomstige beweging bepalen.)
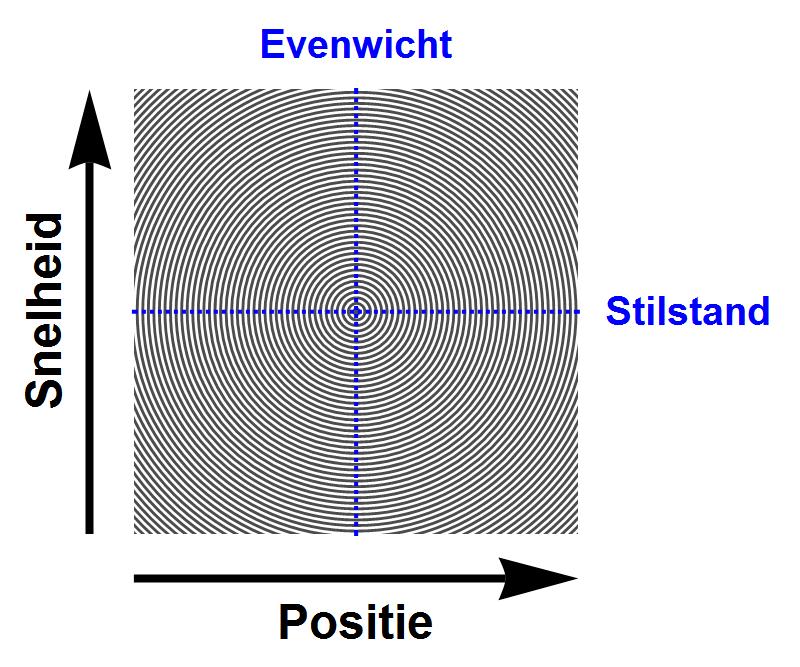
Afbeelding 6. Fasebanen van de harmonische oscillatorDe faseruimte van de harmonische oscillator is opgebouwd uit oneindig veel cirkelvormige banen.
Veel van wat we hier gezien hebben voor het eenvoudige voorbeeld van de harmonische oscillator geldt ook voor algemenere natuurkundige systemen. De faseruimte heeft een even aantal dimensies; de helft daarvan zijn positiedimensies en de andere helft de bijbehorende impulsdimensies. Elk punt in de faseruimte bepaalt een mogelijke beweging van het systeem, en bepaalt die beweging helemaal. De faseruimte is dus een verzameling van een oneindig aantal banen. Wat overigens niet altijd het geval is, is dat de banen weer op dezelfde plaats terugkeren; dit is alleen het geval voor systemen die net als de harmonische oscillator een periodieke beweging uitvoeren.
Dit is het vierde artikel in het dossier Faseruimte. Het vijfde artikel, over de stelling van Liouville, verschijnt binnenkort. Houd dus de website in de gaten!
Afbeelding blokkenschema: © Ril | Stock Free Images & Dreamstime Stock Photos