Faseruimte (3): Klassieke faseruimte

Een faseruimte is een speciaal soort configuratieruimte. In het vorige artikel hebben we het alleen gehad over de posities van de auto’s, maar er zijn natuurlijk allerlei andere eigenschappen waarin we geïnteresseerd kunnen zijn. De belangrijkste daarvan is de snelheid van de auto’s: als we de snelheden weten, en ervan uitgaan dat de auto’s min of meer met constante snelheid bewegen, kunnen we voorspellen waar de auto’s over één seconde, tien seconden, of één minuut zullen zijn.

Een auto kan natuurlijk versnellen of vertragen, dus als we de positie en de snelheid van een auto weten, kunnen we niet precies voorspellen wanneer de auto op een bepaalde plek zal zijn. Veel natuurwetten blijken echter de eigenschap te hebben dat iets dergelijks wel kan. Denk bijvoorbeeld weer aan de biljartballen op het biljartlaken: als we van alle ballen de posities en de snelheden weten, kunnen we precies uitrekenen hoe de ballen verder zullen bewegen. Of neem de zwaartekrachtswetten: als we van een komeet die om de zon draait precies de plaats en de snelheid weten, kunnen we zijn hele toekomstige baan bepalen.

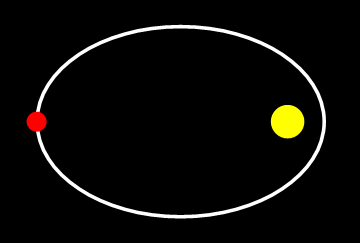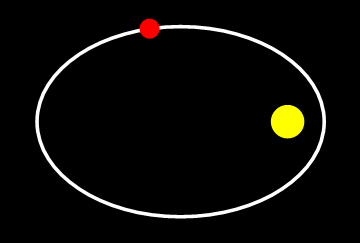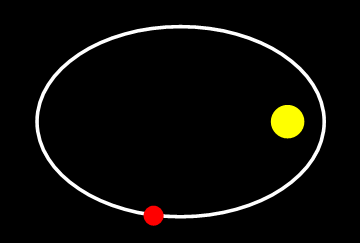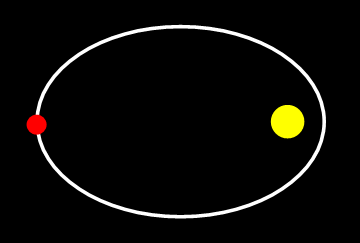
Afbeelding 1. De baan van een komeet om de zonTijdens een omloop veranderen niet alleen de positie en de snelheid van de komeet, maar ook de versnelling. Toch is informatie over alleen de positie en de snelheid voldoende om de hele baan te bepalen.

Laten we dit laatste voorbeeld iets beter bekijken. Het moge duidelijk zijn dat we uit alleen de positie van een komeet niet zijn precieze baan kunnen bepalen. Als we weten dat de komeet zich tien miljoen kilometer van de zon bevindt, weten we bijvoorbeeld nog niet of de komeet op dat moment recht naar de zon toe beweegt, recht ervanaf, of in een richting daar tussenin. We zullen dus op zijn minst ook de snelheid (en richting – in de natuurkunde bedoelen we met “snelheid” altijd óók de richting waarin iets beweegt) van de komeet moeten weten.

Waarom is die informatie voldoende? We moeten de snelheid van de komeet weten om erachter te komen hoe de positie van de komeet verandert. Maar moeten we dan ook niet iets weten over de versnelling van de komeet, om te weten hoe de snelheid verandert? En vervolgens iets over de verandering van de versnelling, enzovoort?

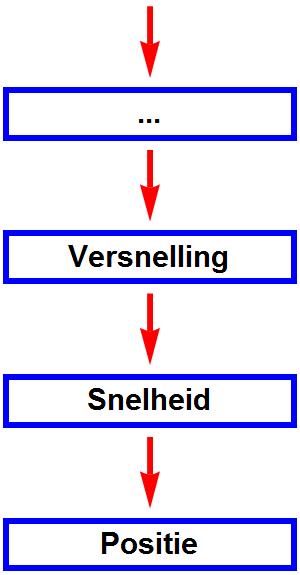
Afbeelding 2. Positie, snelheid, versnelling, …De snelheid van een voorwerp beschrijft  hoe de positie verandert. De versnelling beschrijft hoe de snelheid verandert. Ook de versnelling kan veranderen (al is er geen gangbare naam voor de grootheid die die verandering weergeeft), enzovoort.

Het antwoord op deze vraag is dat we wel degelijk de versnelling van de komeet moeten weten, maar dat deze alleen bepaald wordt door de positie. Dit volgt uit twee bewegingswetten die in de 17e eeuw ontdekt werden door Isaac Newton: de zwaartekrachtwet, die zegt dat de grootte van de zwaartekracht afhangt van de afstand van de komeet tot de zon, en de zogenaamde Tweede Wet van Newton, die zegt dat elke kracht een versnelling veroorzaakt. Samen vertellen deze twee wetten ons inderdaad dat we uit de positie van de komeet zijn versnelling kunnen berekenen. We hoeven die versnelling dus niet apart als eigenschap in ons lijstje op te nemen. Op dezelfde manier wordt de verandering in de versnelling bepaald door de verandering in de positie, enzovoort. De oneindige keten van “veranderingen” in afbeelding 2 bevat dus enorm veel overbodige informatie; we hoeven maar twee gegevens uit die keten te weten om de hele toekomstige baan van de komeet te kunnen bepalen.

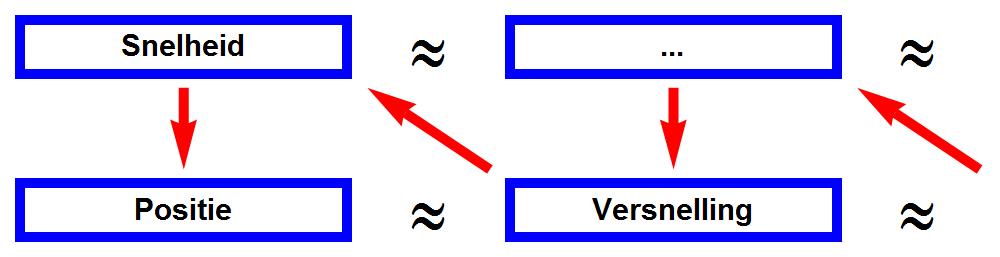
Afbeelding 3. Versnelling en positieIn veel gevallen kunnen we de versnelling van een object bepalen uit zijn positie. Als dat het geval is, hoeven we alleen de positie en de snelheid op een bepaald moment te kennen om de hele toekomstige baan van het object te kunnen bepalen.

Het feit dat de versnelling van de komeet bepaald wordt door zijn positie kan in wiskundige termen als volgt worden geformuleerd: de beweging van de komeet wordt bepaald door een vergelijking van tweede orde. “Tweede orde” wil zeggen dat we twee stappen omhoog moeten gaan in het diagram van afbeelding 2. Als de vergelijking van eerste orde was geweest, zou de snelheid bepaald worden door de positie van de komeet. Als de vergelijking van derde orde was geweest, zou de verandering in de versnelling – in de afbeelding bij gebrek aan een gangbare term aangegeven met “…” – bepaald worden door de positie, enzovoort. Iets preciezer: we noemen een bewegingsvergelijking ook van “tweede orde” als de versnelling bepaald wordt door de positie en de snelheid – in het algemeen mag de grootheid in een bepaald blok bepaald worden door alle blokken eronder.

Het feit dat de zwaartekrachtswetten vergelijkingen van tweede orde zijn, is niet iets dat we kunnen verklaren; het is nu eenmaal het soort wetten dat de natuur “gekozen” heeft. Opvallend is wel dat heel veel andere natuurwetten aan hetzelfde patroon voldoen: alle mechanische (en quantummechanische) systemen hebben bewegingsvergelijkingen van tweede orde, en ook veel systemen in de thermodynamica, hydrodynamica, enzovoort, kunnen door dergelijke vergelijkingen beschreven worden.

Om die reden is het vaak zinvol om configuratieruimtes te gebruiken die zowel de posities als de snelheden van de componenten van het systeem bevatten – maar niet de versnelling of de hogere “blokken” uit afbeelding 2. Elke eigenschap van het systeem wordt op die manier dus gekoppeld aan een tweede eigenschap die de verandering van de eerste aangeeft, en zo komen alle eigenschappen in natuurlijke paren in zo’n configuratieruimte voor. Een dergelijke configuratieruimte wordt een faseruimte genoemd. (Een configuratieruimte die alleen de positie-cooördinaten bevat heet ook wel toestandsruimte.)

Een technische opmerking tot slot: om de wiskunde wat eleganter te maken, wordt meestal niet met snelheden gerekend, maar met impulsen. De impuls van een biljartbal of een komeet is zijn snelheid vermenigvuldigd met zijn massa. (Ter herinnering: “massa” is de natuurkundige term voor wat we in het dagelijks leven vaak “gewicht” noemen: de hoeveelheid materie – in kilogrammen – waaruit een voorwerp bestaat.) Zolang de massa van een biljartbal of een komeet niet verandert, verschillen de begrippen snelheid en impuls alleen door die (constante) vermenigvuldigingsfactor, en maakt het voor de faseruimte dus weinig uit welk begrip we hanteren. Wanneer de massa van een object veranderlijk is (bijvoorbeeld doordat de komeet in de buurt van de zon smelt en een deel van zijn massa verliest) is het wiskundig eenvoudiger om met de impuls te rekenen dan met de snelheid. Vanaf nu zullen we als we het over paren van eigenschappen hebben, dus spreken over posities en de bijbehorende impulsen. In de meeste gevallen kan het geen kwaad om in gedachten het woord “impuls” te vervangen door “snelheid”.

Dit is het derde artikel in het dossier Faseruimte. In het vierde artikel zullen we een eenvoudig voorbeeld van een faseruimte zien: dat van de harmonische oscillator.