
Afbeelding 1. Een kunstmatig molecuul.De golffunctie van een kunstmatig molecuul met topologisch beschermde elektronische hoektoestanden (hoge pieken).
Een van de huidige natuurkundige interessegebieden is het ontwikkelen van quantumbits (qubits) voor quantumcomputers. Zeker nu Google met Sycamore quantumsuperioriteit meent te hebben bereikt, zijn claims over quantumcomputers overal te vinden in de media. Een van de moeilijkheden voor het maken van goede qubits is quantumdecoherentie: het effect dat er bij quantumtoestanden informatie verloren gaat aan de omgeving. Het gevolg is dat het tijdens een berekening in een quantumcomputer onbekend is of er informatie verloren is gegaan en daardoor je berekening niet is gegaan zoals je dacht: je komt misschien op een verkeerd antwoord uit. Een mogelijke oplossing die tegenwoordig veel wordt onderzocht, is om topologisch beschermde toestanden als qubits te gebruiken. Deze toestanden zijn extreem stabiel en zijn beschermd door een bepaalde symmetrie in het materiaal. Door deze bescherming blijven de qubits coherent en kun je er berekeningen mee doen – althans, dat is de theorie. Recent is er een stap voorwaarts gemaakt in het construeren van een topologisch beschermde elektronische toestand in een kunstmatig molecuul – zie afbeelding 1. In dit artikel bespreek ik hoe je precies een kunstmatig molecuul met deze zogeheten hoektoestanden kan maken.
Topologie
In een eerder artikel op deze website zijn topologische isolatoren al eens besproken. Dit zijn materialen die minimaal twee verschillende fasen hebben. ‘Fasen’ zijn verschillende toestanden waarin het materiaal kan zijn – voor water kennen we bijvoorbeeld fasen als ‘vast’, ‘vloeibaar’ en ‘damp’. Een topologische isolator is in de ene fase een gewone isolator (geleidt geen elektriciteit) en heeft in de andere fase metaalachtige randtoestanden. Als het materiaal in deze laatste fase is, kan het dus langs de randen een elektrische stroom geleiden. Zelfs wanneer er onzuiverheden (zoals defecten in de molecuulstructuur) op de rand zijn, is de grootte van de randstroom exact te berekenen. Sterker nog: het blijkt dat deze stromen ontzettend stabiel zijn en zich niets aantrekken van onzuiverheden en omgevingsfactoren. Dit is heel anders dan bij een stroom in een draad: als er iets verandert in de draad zul je direct kunnen meten dat er minder stroom loopt. Vaak worden deze topologische fasen vergeleken met het verschil tussen een donut en een koffiekopje aan de ene kant, en een bol aan de andere kant. Een donut kun je omvormen tot een koffiekopje omdat ze allebei een gat hebben. Je zal alleen nooit een bol in een donut kunnen veranderen, tenzij je iets drastisch doet zoals een gat knippen in de bol. Net zo goed kun je deze topologische fasen niet verwijderen zonder iets drastisch aan het systeem te veranderen: in dit geval het breken van de beschermende symmetrie.
In 2017 deden de onderzoekers Wladimir Benalcazar, Andrei Bernevig en Taylor Hughes een nieuw voorstel voor het vinden van topologische fasen. Tot dan toe waren er alleen maar randtoestanden beschreven waarvan de elektronen zich in 1 dimensie lager verplaatsten dan de dimensie van het materiaal zelf. Bijvoorbeeld: in het quantum-Hall-effect is er sprake van een 2-dimensionaal oppervlak waarbij de randtoestanden langs de randen bewegen in een 1-dimensionale ruimte, een lijn. Er zijn ook 3-dimensionale materialen (kubussen) met 2-dimensionale oppervlaktestromen, en zo verder. Het nieuwe idee in 2017 was om deze fasen breder te definiëren en op een nieuwe manier inzicht te geven in bijvoorbeeld 0-dimensionale (puntvormige) hoektoestanden in een 2-dimensionaal oppervlak of 1-dimensionale randstromen in 3 dimensies. Deze toestanden moeten uiteraard ook beschermd worden door de symmetrie van het kristal.
Direct gingen andere wetenschappers op zoek naar materialen waarin ze deze ‘hogere-orde topologische toestanden’ konden zien. Daarnaast kwamen er veel voorstellen uit de theoretische hoek met verschillende symmetrieën die een materiaal zou moeten hebben voor hogere-orde topologie. En dat is precies het punt waarop het soms erg lastig wordt: hoe kun je in de enorme zee van verschillende materialen precies het juiste materiaal vinden waar je naar op zoek bent zonder dat je last hebt van andere (vaak erg ingewikkelde) effecten die ook in het materiaal zitten? Dit is waar een quantumsimulator van pas komt.
Wat is een quantumsimulator?
In 1959, 60 jaar geleden, gaf Richard Feynman een befaamde lezing en sprak daarin de woorden uit “There is plenty of room at the bottom”. Hiermee bedoelde hij dat, wanneer we weten hoe we individuele atomen kunnen manipuleren, er een wereld vol mogelijkheden opengaat. Inmiddels kunnen we atomen zo neerzetten dat we een kunstmatig molecuul maken. Zo’n kunstmatig molecuul bestaat niet per se op de gebruikelijke manier uit atomen als bouwstenen, maar is een slimme methode om elektronen zo te vangen dat ze exact dezelfde eigenschappen krijgen als wanneer ze in een echt molecuul zouden zitten. Je hoeft dus niet meer op zoek naar het materiaal met de perfecte symmetrie, je kunt het gewoon simuleren! Deze quantumsimulatoren worden tegenwoordig veel gebruikt en zijn er in allerlei soorten en maten, waarbij zowel fermionen (zoals elektronen) als bosonen (zoals fotonen) gebruikt kunnen worden. Door deze quantumsimulatoren is het veel eenvoudiger geworden om theoretische modellen experimenteel te bewijzen of te ontkrachten.
Een manier om een kunstmatig molecuul te maken, is door gebruik te maken van vrije elektronen die op een koperoppervlak zitten. Experimenteel kunnen er moleculen koolstofmonoxide (CO) op het koperoppervlak gedampt worden. Deze CO-moleculen kunnen vervolgens met een scanning tunneling-microscoop zeer precies verplaatst worden van de ene plek naar de andere. (IBM kan dit intussen zelfs zo goed dat ze er ’s werelds kleinste film van hebben gemaakt.) De vrije elektronen op het koperoppervlak botsen steeds tegen deze moleculen aan en worden hierdoor weerkaatst. Dit principe kan vervolgens goed gebruikt worden: door het maken van bijvoorbeeld een cirkel van atomen zal er in het midden van de cirkel een resonantie optreden en zal daar een piek zijn in de elektronische golffunctie – zie afbeelding 2. In het midden van de cirkel zijn vervolgens alle elektronische toestanden te zien die ook in een echt 2-dimensionaal atoom te vinden zijn. De ring van moleculen wordt ook wel een quantumkraal genoemd met erbinnen de quantumweerspiegeling. Het effect is voor het eerst experimenteel gemeten in 1993 met een ring van ijzeratomen.
Het kunstmatige molecuul doet sterk denken aan het model van een ‘deeltje in een doosje’, zie afbeelding 2. De CO-moleculen zijn in dit geval effectieve muren waar de elektronen niet doorheen kunnen. Wanneer er een elektron in dit doosje zit, leidt de vorm van het doosje ertoe dat alleen bepaalde golffuncties met daarbij behorende energieën mogelijk zijn. Het verschil met het traditionele deeltje in een doosje is dat de potentiaal die de CO-moleculen veroorzaken niet oneindig hoog is en dat een CO-molecuul rond is in plaats van een lijn. Effectief kun je dit zien alsof de elektronen gevangen zitten in een omgekeerde muffinbakvorm. Er zit in deze vorm ongeveer 1 elektron per 1,4 nm2. Door het precies plaatsen van CO-moleculen kun je dus een kunstmatig atoom maken dat ‘in de ruimte tussen de CO-moleculen zit’. Vervolgens worden deze atomen naast elkaar neergezet om een kunstmatig molecuul te maken.
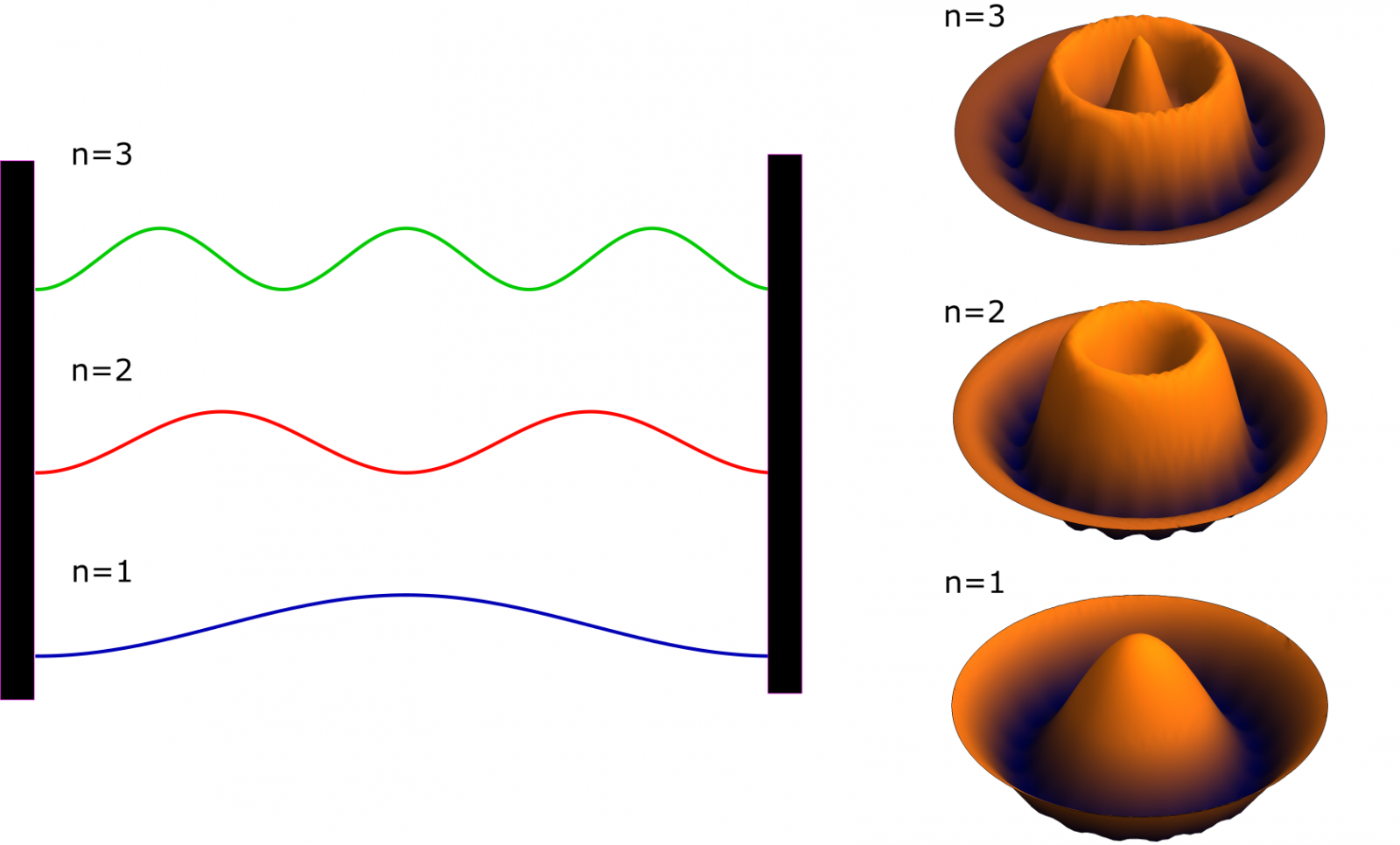
Afbeelding 2. Deeltje in een doosje en een kunstmatig molecuul.De gekwadrateerde golffunctie van een deeltje in een doosje (links) en van een kunstmatig atoom (rechts). De donkergekleurde cirkel geeft de CO-moleculen weer. De golffuncties van een deeltje in een 1-dimensionaal doosje zijn sinussen en worden gelabeld door het quantumgetal n (een geheel getal). De eerste golffuncties van het kunstmatige atoom hebben eenzelfde vorm.
Het maken van een hogere-orde topologische isolator
Tot slot moet er dan een ontwerp gemaakt worden voor een hogere-orde topologische isolator. Hoe zet je namelijk de CO-moleculen neer waardoor de kunstmatige atomen precies in het juiste rooster met de correcte verbindingen komen? Door eerst een computersimulatie te doen van de elektronen in een ‘muffinbakvorm’ wordt gekeken welke configuratie het beste is. Een computersimulatie is namelijk veel sneller dan het doen van het echte experiment. Op het moment dat het duidelijk is op welke manier de CO-moleculen geplaatst moeten worden voor het gewenste effect, gaan de experimentatoren aan de slag.
De configuratie voor een hogere-orde topologische isolator is te zien in afbeelding 3. Effectief gezien kunnen de elektronen overspringen van het ene naar het andere kunstmatige atoom. Wanneer de atomen dicht bij elkaar zitten, is de kans groter dan een elektron kan overspringen dan wanneer ze verder van elkaar staan. Dit al dan niet overspringen resulteert in een sterke of zwakke verbinding tussen atomen. In het kunstmatige rooster wordt dit effect gecreëerd door de CO-moleculen dicht bij elkaar te zetten of juist verder van elkaar: wanneer de CO-moleculen dicht bij elkaar staan is er minder overlap tussen de elektrongolven van de atomen en dus een zwakkere verbinding – de rode lijn in afbeelding 3. Als de CO-moleculen juist verder uit elkaar staan is er meer overlap tussen de elektronen en is er een sterke verbinding – de blauwe lijn in afbeelding 3. Hierdoor ontstaat een molecuul met zowel zwakke als sterke verbindingen. De theorie voorspelt dat dit molecuul topologisch beschermde toestanden heeft in de hoek, als er een zwakke verbinding wordt gemaakt met de hoek.
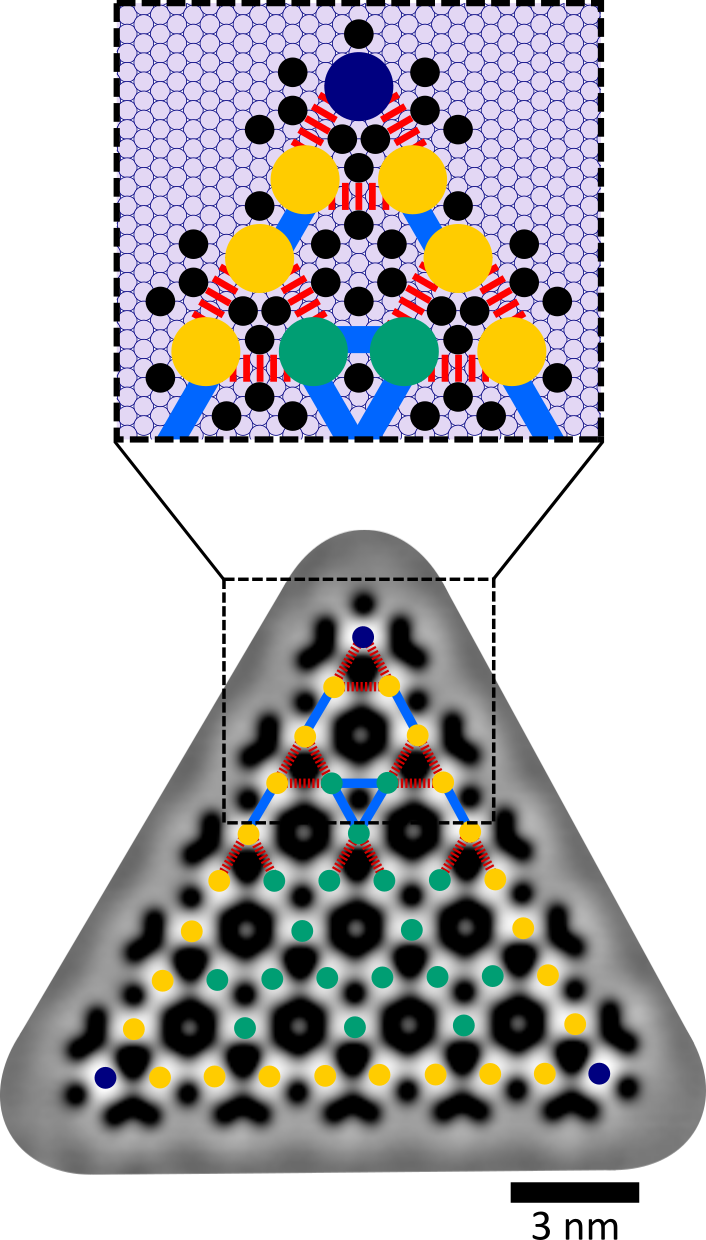
Afbeelding 3. Een hogere-orde topologische isolator.Schematisch ontwerp van een kunstmatige hogere-orde topologische isolator. De CO-moleculen (zwart) weerkaatsen de elektronen waardoor er kunstmatige atomen ontstaan. Er zijn bulk- (groen), rand- (geel) en hoekatomen (donkerblauw). Deze koppelen aan elkaar via een sterke verbinding (lichtblauw) of een zwakke verbinding (rood). De achtergrond geeft het koperrooster weer.
Dit is precies wat er ook wordt gedetecteerd in het experiment. Met de microscoop is er een piek te zien van de golffunctie in de hoeken van het molecuul, zoals weergegeven in afbeelding 1 bovenaan. Om te onderzoeken of deze toestanden beschermd zijn, worden er vervolgens allerlei defecten toegevoegd door extra CO-moleculen te plaatsen in het rooster: zie afbeelding 4. Deze defecten hebben geen enkele invloed op de hoektoestanden terwijl ze wel een effect hebben op alle andere toestanden in het molecuul. Hiermee wordt de stabiliteit van de hoektoestand bevestigd. Tot slot kun je ook nog extra hoektoestanden maken door een hoek kunstmatig aan de driehoek vast te plakken, zoals onderin in afbeelding 4 te zien is. Op deze manier zijn er zeer stabiele hoektoestanden gemaakt.
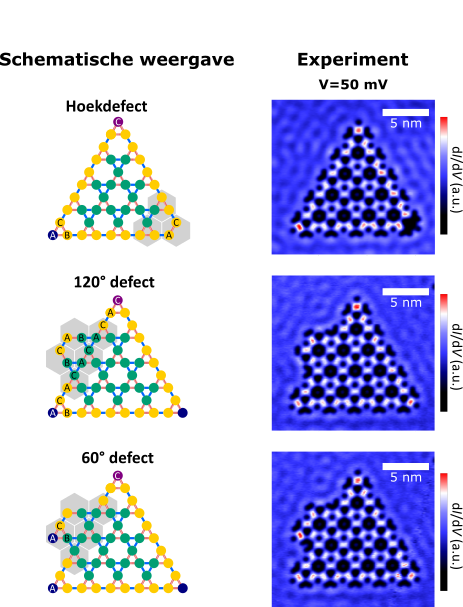
Afbeelding 4. Stabiliteit van de hoektoestanden.Onderzoek naar de stabiliteit van de hoektoestanden. Ondanks het inbouwen van defecten blijven de hoektoestanden bestaan. Het is mogelijk om een hoektoestand weg te halen terwijl de andere aanwezig blijven (bovenaan). Daarnaast kun je een stuk aan het molecuul vastmaken, maar dit heeft geen invloed op de hoektoestanden (midden). Tot slot kun je een extra hoektoestand maken door een nieuwe hoek aan het molecuul vast te maken (onder).
Terug naar waar we dit verhaal mee begonnen: de quantumcomputer. De hier gemaakte toestanden zijn weliswaar nog geen qubits waar informatie in opgeslagen kan worden, maar het principe waarmee deze hoektoestanden kunnen worden gemaakt, is goed begrepen en kan nu worden uitgebreid om er verder onderzoek naar te doen. Voor echte quantumberekeningen is het bijvoorbeeld nodig dat deze toestanden om elkaar heen worden gedraaid; of dat mogelijk is in deze quantumsimulator is nog de vraag. Daarnaast zijn deze qubits niet supergeleidend waardoor de berekeningen minder efficiënt zouden zijn. Desalniettemin is dit een eerste stap voor het maken van elektronische topologisch beschermde toestanden in een 2-dimensionaal materiaal. Daarnaast biedt de quantumsimulator ook mogelijkheden voor het maken van allerlei andere kunstmatige moleculen, bijvoorbeeld moleculen die niet in de natuur te vinden zijn maar die wel waanzinnig interessant zijn, zoals fractalen. Een fractaal is een object met een niet-gehele dimensie, zoals 1,58. Met dezelfde techniek van de hierboven beschreven quantumsimulator is recent ook een ‘Sierpinski-driehoek’ gemaakt met een fractale dimensie. Hoe dat precies zit, kun je hier verder bekijken.
Referentie
Robust zero-energy modes in an electronic higher-order topological insulator
S. N. Kempkes, M. R. Slot, J. J. van den Broeke, P. Capoid, W. A. Benalcazar, D. Vanmaekelbergh, D. Bercioux, I. Swart, C. Morais Smith, Nature Materials (2019).