Quantumfysica (8): Tunnelen

We hebben in de afgelopen artikelen al diverse aspecten van de quantummechanica belicht. In al die aspecten speelt het feit dat quantummechanica gaat over kansen een centrale rol. In de klassieke natuurkunde is het zo dat een systeem altijd in één enkele toestand is: een deeltje is op plaats A, of op plaats B, of op plaats C, enzovoort. In de quantummechanica kan een deeltje zowel op plaats A als op plaats B als op plaats C zijn. De quantummechanische golffunctie kent aan elk van die plaatsen een bepaalde kans toe.

In dit artikel zullen we zien dat dit kansbegrip ertoe leidt dat ook processen die klassiek gezien helemaal niet mogelijk zijn, quantummechanisch kunnen voorkomen. Laten we bijvoorbeeld eens kijken naar het klassiek natuurkundige systeem in afbeelding 1 hieronder. We zien een rode bal die rolt door een berglandschap. (We kunnen de animatie ook abstracter zien als weergave van bijvoorbeeld een elementair deeltje dat een afstotende en een aantrekkende kracht ondervindt, en daardoor tussen twee posities heen-en-weertrilt.) De rode bal heeft een bepaalde hoeveelheid energie; die energie wordt steeds omgezet tussen bewegingsenergie (of kinetische energie) als het deeltje in het dal is en zijn hoogste snelheid heeft, en zwaarte-energie (of potentiële energie) als het deeltje één van de wanden is opgerold en zijn hoogste punt heeft bereikt.

Afbeelding 1. Een bal in een berglandschap.De bal zet continu kinetische in potentiële energie om, en omgekeerd. De totale hoeveelheid energie is kleiner dan de energie die nodig is om de top van de berg te bereiken; de bal zal dus altijd heen en weer blijven rollen.

We nemen voor het gemak aan dat de bal geen wrijving ondervindt; in dat vereenvoudigde geval zal de bal eeuwig heen en weer blijven rollen. De bal zal natuurlijk nooit over de berg heen rollen: hij heeft eenvoudigweg niet genoeg energie om hoog genoeg te komen.

Hoe ziet ditzelfde systeem er in de quantummechanica uit? Dat zien we in afbeelding 2. Als we alleen de totale hoeveelheid energie van de bal kennen, kan hij nog op allerlei verschillende plaatsen zijn, en allerlei verschillende snelheden hebben. Om precies uit te rekenen wat de kansen op al die plaatsen en snelheden zijn, moeten we de Schrödingervergelijking oplossen – een wiskundige opgave die met de nodige achtergrondkennis (en voor niet al te ingewikkelde “berglandschappen”) uitgevoerd kan worden. Het resultaat zien we geschetst in de grijze grafiek in afbeelding 2. Waar die grafiek het hoogst is, is de kans om het deeltje aan te treffen het grootst; waar de grijze grafiek laag is, is de kans om het deeltje aan te treffen heel klein.

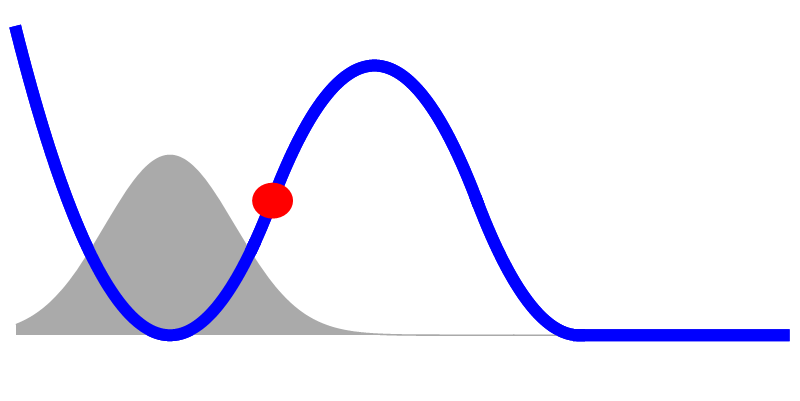
Afbeelding 2. Een quantummechanische bal in een berglandschap.De grijze grafiek geeft de kansverdeling van de positie van de bal weer. Waar die grafiek het hoogst is, is de kans om het deeltje aan te treffen het grootst; waar de grijze grafiek laag is, is de kans om het deeltje aan te treffen heel klein.

Als we goed kijken naar de grijze grafiek in afbeelding 2 valt iets bijzonders op. We zouden misschien verwachten dat die grafiek er meer uit zou zien als in afbeelding 3. In die afbeelding geeft de grijze grafiek weer een kansverdeling weer, maar nu is het zo dat alleen de posities waar we het deeltje klassiek kunnen aantreffen, ook een kans groter dan nul hebben in het quantummechanische systeem. In afbeelding 2 is dat niet zo: er zijn ook klassiek onmogelijke posities waarop we (met heel kleine kans) het deeltje zouden kunnen aantreffen.

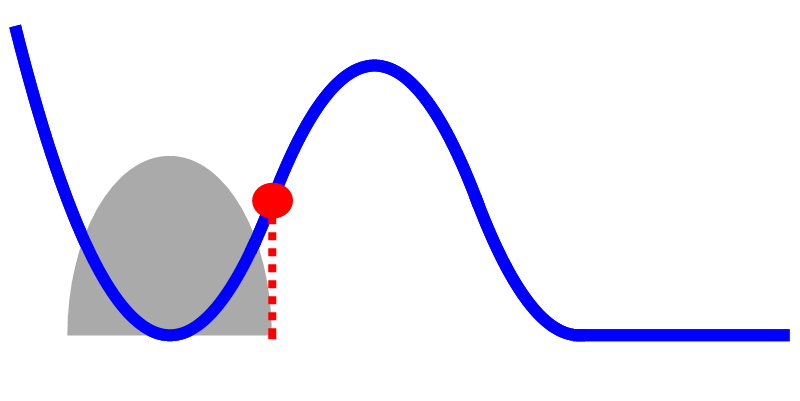
Afbeelding 3. Een quantummechanische bal in een berglandschap (incorrect).In plaats van de grafiek in afbeelding 2 zouden we wellicht eerder een grafiek als de bovenstaande verwachten. De rode bal is op zijn rechter keerpunt getekend; posities die nog verder naar rechts liggen hebben in deze grafiek een kans die gelijk is aan nul.

Waarom geeft afbeelding 2 het juiste quantummechanische antwoord, en niet afbeelding 3? We kunnen daarop een wiskundig en een natuurkundig antwoord geven. Het wiskundige antwoord is als volgt. In afbeelding 3 heeft de kansverdeling een “knik” op het punt waar die nul wordt, terwijl de kansverdeling in afbeelding 2 “glad” is en nergens zo’n knik heeft. In nette wiskundige termen: de grafiek in afbeelding 2 is op elk punt differentieerbaar, de grafiek in afbeelding 3 is dat niet. Met wat wiskunde is het mogelijk om aan te tonen dat, zolang het berglandschap zelf “glad” is, de oplossingen van de Schrödingervergelijking ook “glad” moeten zijn. Een knik zoals in afbeelding 3 is dus niet mogelijk.

Dat wiskundige antwoord is natuurlijk niet erg bevredigend; het geeft ons geen intuïtie voor waarom het deeltje quantummechanisch ook op klassiek onmogelijke plaatsen kan worden aangetroffen. Laten we dus ook een minder exact maar meer fysisch argument geven. Stel dat we de bal op een gegeven moment aantreffen op het hoogste punt in zijn baan. Klassiek verwachten we dat de bal daar exact stil ligt: hij is net gestopt met omhoog rollen, en gaat beginnen aan zijn weg omlaag. Quantummechanisch kan het echter niet zo zijn dat de bal op dat punt exact stil ligt: in dat geval zouden we immers zowel de positie (het keerpunt) als de snelheid (nul) van de bal exact kennen, en dat is in tegenspraak met het onzekerheidsprincipe van Heisenberg. Ook in het hoogste punt van de baan is er dus een kansverdeling voor de snelheid van de bal, en er zal daarom een kleine kans zijn dat de bal vanaf dat punt nog iets verder omhoog rolt. Zo kan de “quantumbal” dus komen op plaatsen die de “klassieke bal” nooit kan bereiken.

Op deze manier is het zelfs mogelijk dat de bal op een gegeven moment de top van de berg bereikt, en aan de andere kant weer naar beneden rolt. Dit proces wordt tunnelen genoemd: het is alsof de bal een “tunnel” door de berg heen heeft gegraven, en zo aan de andere kant is uitgekomen. Dit is een extreem verschil tussen de klassieke natuurkunde en de quantummechanica: klassiek gezien zullen we de bal nooit aan de andere kant van de berg aantreffen; quantummechanisch zal dat, als we maar lang genoeg wachten, altijd een keer gebeuren. Het “maar lang genoeg wachten” is hier wel cruciaal: voor een grote bal in een daadwerkelijk berglandschap zal het hier gaan om een tijdsschaal die de huidige leeftijd van het heelal ver overtreft.

Op macroscopische schaal zullen we het tunneleffect dus nooit ervaren, maar op microscopische schaal ligt dat heel anders. Als we afbeelding 1 interpreteren als de beweging van één enkel quantumdeeltje, dat door twee krachten tussen twee keerpunten heen-en-weertrilt, zal de kans dat het deeltje op een gegeven moment uit de “potentiaalput” tunnelt veel groter zijn. Een voorbeeld waarin dit gebeurt is radioactief verval: als we lang genoeg wachten zullen bepaalde atomen door exact dit proces een aantal van hun kerndeeltjes verliezen, ondanks dat dat proces klassiek gezien onmogelijk is. Als de energiebarrière die overwonnen moet worden groot is, kan dit nog steeds heel lang duren: een uranium-238-atoom vervalt bijvoorbeeld gemiddeld na ruim 4 miljard jaar tot een thorium-234-atoom. Is de energiebarrière laag, dan kan dit verval in een fractie van een seconde plaatsvinden. Zie deze lijst van vervaltijden op Wikipedia om te zien hoe enorm dergelijke tijdschalen uiteen kunnen lopen.

Het tunneleffect kent ook technologische toepassingen. Het beroemdste voorbeeld is waarschijnlijk de scanning tunneling microscope (STM), een microscoop waarin de elektronenstroom als gevolg van tunnelen tussen een afleesnaald en een te onderzoeken oppervlak wordt gemeten. De grootte van deze stroom hangt heel gevoelig af van de afstand tussen de naald en het oppervlak, dus door de naald over het oppervlak te laten bewegen kan het oppervlak tot op fracties van een atoomgrootte nauwkeurig gemeten worden. In afbeelding 4 zijn bijvoorbeeld de individuele atomen in het oppervlak van een siliciumcarbidekristal te zien.

Afbeelding 4. Het atoomrooster in een siliciumkristal.Deze afbeelding is gemaakt met een scanning tunneling microscope: we zien de individuele atomen in het kristalrooster. Afbeelding: Guillaume Baffou.

Kortom: tunnelen is een typisch quantummechanisch verschijnsel dat in veel natuurkundige toepassingen een rol speelt. Het concept toont mooi aan dat quantummechanica gaat over objecten die onwaarschijnlijk klein zijn, maar dat de toepassingen van quantumeffecten desalnietemin in ons dagelijks leven een rol kunnen spelen. In het volgende artikel behandelen we een quantumtoepassing die op dit moment nog niet in ons dagelijks leven voorkomt, maar dat wellicht in de toekomst wel gaat doen: quantumcomputers.

Dit is het achtste artikel uit het dossier Quantumfysica. In het negende artikel bespreken we een belangrijk toepassingsgebied van de quantummechanica: dat van quantumcomputers.

Afbeelding blokkenschema: Manfred Werner.