Quantumfysica (6): Het onzekerheidsprincipe

Een belangrijke en verrassende eigenschap van de quantummechanica werd door de Duitse fysicus Werner Heisenberg in 1927 ontdekt. Dit beroemde resultaat van Heisenberg staat tegenwoordig bekend als het onzekerheidsprincipe. Het zegt iets over de hoeveelheid “klassieke” informatie die we uit een quantummechanisch systeem kunnen halen.

Afbeelding 1. Werner Heisenberg.Werner Heisenberg (midden) in gesprek met twee andere grootheden uit de geschiedenis van de quantummechanica: Niels Bohr (links) en Wolfgang Pauli (rechts). Bron: American Institute of Physics, Emilio Segrè Visual Archives.

Het principe dat Heisenberg ontdekte, is een gevolg van het feit dat we het in de quantummechanica nooit alleen over deeltjes hebben, maar ook altijd over de golven die een kansverdeling voor die deeltjes beschrijven. Het idee van kansgolven is besproken in het vierde artikel uit deze serie. Golven hebben een belangrijke eigenschap die deeltjes niet hebben. Die eigenschap kunnen we al zien bij “klassieke” golven zoals watergolven. Gooi een zware steen in een diepe sloot, zodat een flinke golf in de lengterichting van de sloot ontstaat. Terwijl de golf zich voortplant, zal opvallen dat die steeds minder uitgesproken wordt: de piek zal minder hoog worden, en de golf zal uitgespreid worden over een groter deel van de sloot. Het is overigens van belang dat de sloot goed diep en de golf groot is. Bij kleine golven in ondiepe sloten zal dit “uitspreideffect” maar heel klein zijn, en zal de golf pas na heel lange tijd uitdoven – een effect dat rond 1895 werd beschreven door de Nederlandse wiskundigen Diederik Korteweg en Gustav de Vries.

Afbeelding 2. Een watergolf.Een golf in diep water spreidt zich na verloop van tijd uit en wordt minder hoog. De reden hiervoor is dat het voorste deel van de golf zich met een hogere snelheid voortplant dan het achterste deel.

Wat gebeurt hier nu precies? De golf in het water blijkt niet precies één vaste snelheid te hebben. Delen van de golf hebben een iets andere snelheid dan andere delen, waardoor na een bepaalde tijd het ene deel van de golf zich al iets verder heeft voortgeplant dan het andere deel. Het uitspreideffect is dus een gevolg van het feit dat de golf niet een exacte snelheid heeft, maar als het ware een “bereik” van snelheden.

Hoe meer uitgesproken (steiler) de golf aan het begin van dit experiment is, hoe groter dit effect zal zijn. Een enorm hoge, smalle golf zal al heel snel uitwaaieren en veel lager en breder worden. Met andere woorden: als we de plaats van de golf aan het begin van het experiment heel nauwkeurig kunnen bepalen, doordat er een heel uitgesproken piek is, kunnen we juist de snelheid niet heel nauwkeurig bepalen. Na een paar seconden zal het voorste deel van zo’n golf al veel verder zijn dan het achterste deel.

Het omgekeerde blijkt ook te gelden. Stel dat we een golf willen construeren waarvan we heel nauwkeurig de snelheid willen bepalen. Met andere woorden: we willen dat de golf zijn vorm behoudt, en in die vorm zich met vaste snelheid door het water voortplant. Dat blijkt te kunnen als we de golf een heel specifieke vorm geven, namelijk de vorm van een sinus (afbeelding 3) met regelmatige pieken en dalen. Zo’n golf behoudt in de loop van de tijd inderdaad zijn vorm, en heeft dus een duidelijk bepaalde snelheid, maar tegelijk kunnen we niet duidelijk een plaats aan de golf toekennen – de verschillende pieken van de golf bevinden zich immers op heel verschillende plaatsen.

Afbeelding 3. Een sinusgolf.Een sinusgolf behoudt zijn vorm, en heeft dus een goed gedefinieerde snelheid. Tegelijkertijd is het onmogelijk om een eenduidige plaats aan zo’n golf toe te kennen.

Kortom: geven we een watergolf een heel duidelijk bepaalde plaats, dan is zijn snelheid niet heel nauwkeurig bepaald, en geven we hem een heel duidelijk bepaalde snelheid, dan is zijn plaats niet heel nauwkeurig bepaald. Het blijkt onmogelijk te zijn om een golf te maken die zowel een heel nauwkeurig bepaalde plaats als een heel nauwkeurig bepaalde snelheid heeft.

Heisenberg vroeg zich af of een dergelijk verschijnsel zich ook bij quantumgolven zou voordoen. Om die vraag te beantwoorden, moest natuurlijk eerst precies bekend zijn hoe zo’n quantumgolf zich in de loop van de tijd zou voortplanten. Was dat bekend? Jazeker! Erwin Schrödinger had immers in 1925 zijn beroemde vergelijking opgeschreven (zie het vorige artikel), en die vergelijking beantwoordt precies deze vraag. Als de vorm van de quantumgolf op een bepaald tijdstip bekend is, kan met de Schrödingervergelijking exact berekend worden hoe die vorm zich in de loop van de tijd voortplant.

Heisenberg sloeg dus aan het rekenen met de Schrödingervergelijking, en liet uiteindelijk zien dat voor quantummechanische golven exact hetzelfde geldt als voor “klassieke” golven. Als we de positie van zo’n golf (en dus van het bijbehorende deeltje) heel nauwkeurig kunnen bepalen, kunnen we de snelheid niet heel nauwkeurig bepalen, en omgekeerd. Hij wist dit resultaat heel nauwkeurig weer te geven in de volgende formule:

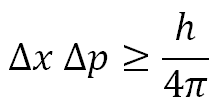
Hierin staat Δx voor de onzekerheid in de plaats. Heisenberg werkte met een heel nauwkeurige wiskundige definitie van dat begrip (de zogenaamde standaarddeviatie), maar voor ons is het voldoende om die onzekerheid te zien als de “breedte” van de golffunctie op een bepaalde hoogte – zie afbeelding 4. Het symbool Δp staat op dezelfde manier voor de onzekerheid in de snelheid – of nog iets preciezer: de onzekerheid in de impuls, die zelf weer gelijk is aan de snelheid van het deeltje maal zijn massa.

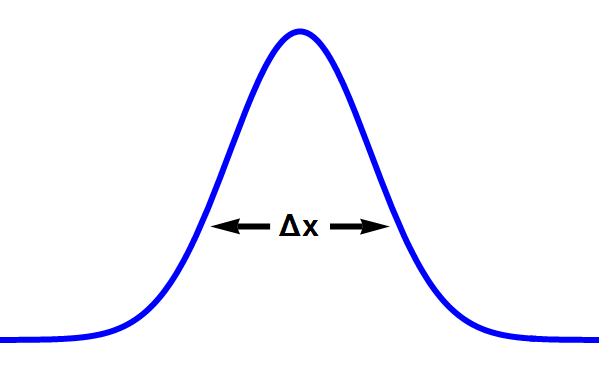
Afbeelding 4. De breedte van een golffunctie.Heisenberg gebruikte een heel precieze wiskundige definitie van de breedte van een golffunctie: de zogeheten standaarddeviatie. Voor ons volstaat een grof beeld: we nemen een bepaalde, vooraf vastgelegde hoogte, en meten de breedte van de golffunctie op die hoogte.

Wat Heisenberg dus liet zien, was dat het product van de twee onzekerheden altijd een bepaalde minimale waarde heeft, gegeven door de rechterkant van de vergelijking. Aan die rechterkant zien we de constante van Planck (zie het tweede artikel uit deze serie) terug. Verder staan er de getallen 4 en π. De rechterkant van Heisenberg’s relatie heeft dus een heel kleine waarde: ongeveer 0,527 x 10^-34 Js.

Kortom: we kunnen quantumgolven zo construeren dat zowel de onzekerheid in de plaats (Δx) als de onzekerheid in de snelheid (weergegeven in Δp) enorm klein zijn. Toch kunnen we nooit helemaal exact zowel de plaats als de snelheid van een quantumdeeltje bepalen: de onzekerheden blijven altijd iets groter dan 0. Vanwege de enorm kleine getallen merken we in het dagelijks leven zelden iets van het onzekerheidsprincipe. Pas op microscopisch niveau speelt het principe een belangrijke rol. Vanuit een fundamenteel oogpunt is het natuurlijk wel een schokkende ontdekking dat we nooit “volledige informatie” over plaats en snelheid van een deeltje kunnen krijgen!

Het onzekerheidsprincipe van Heisenberg is maar één van de vele punten waarop de quantumfysica essentieel verschilt van de klassieke natuurkunde. In de komende artikelen zullen we nog een aantal andere belangrijke verschillen bespreken.

Dit is het zesde artikel uit het dossier Quantumfysica. In het zevende artikel hebben we het over verstrengeling – een schijnbaar paradoxaal begrip, waar Einstein oorspronkelijk de nodige kritiek op had.