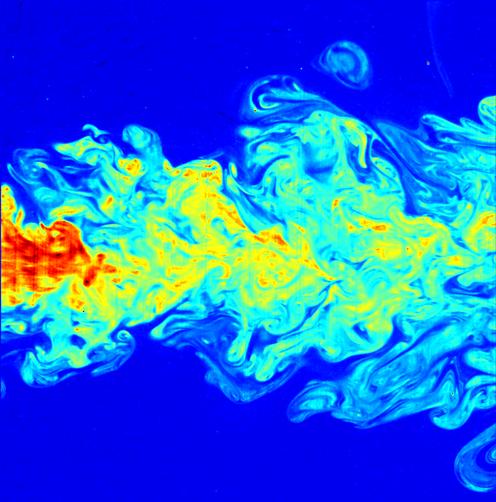
Afbeelding 1. Een turbulente vloeistofstroom.Bron: Wikipedia. C. Fukushima and J. Westerweel, Technische Universiteit Delft.
Navier-Stokesvergelijking
De Navier-Stokesvergelijking, die in dit dossier over hydrodynamica al uitgebreid ter sprake is gekomen, volgt uit behoudswetten in de natuurkunde, namelijk massabehoud en impulsbehoud. De vergelijking heeft een ietwat ingewikkelde vorm, maar past toch zonder problemen op een enkele regel. In haar volle glorie ziet de Navier-Stokesvergelijking er als volgt uit:
![]()
Ter herinnering: om die vergelijking (die we hier verder niet in detail zullen bespreken) af te leiden, moest worden aangenomen dat de vloeistof niet samendrukbaar is en dat er geen externe krachten zoals de zwaartekracht zijn. Dat zijn overigens geen essentiële aannames – ook zónder die aannames kan een vergelijking worden opgeschreven – maar ze versimpelen het antwoord wel. De bovenstaande formule beschrijft een verband tussen vier grootheden: ρ is de dichtheid van de vloeistof, v de snelheidsvector, p de druk en η de viscositeit, die we ook al in het vorige artikel tegenkwamen.
De Navier-Stokesvergelijking vormt de basis voor de beschrijving van veel vloeistoffen, en beschrijft in principe ook turbulente stromingen. Het is deze vergelijking die je in één klap miljonair kan maken, mits je het al dan niet bestaan van oplossingen wiskundig kunt bewijzen. Ik zou uren over deze vergelijking kunnen praten, en over hoe fascinerend het is dat we slechts een enkele vergelijking nodig hebben om alles wat stroomt ermee te kunnen beschrijven, maar dat ga ik in dit artikel niet doen. Ik wil daarentegen aandacht besteden aan een markant verschijnsel, verscholen in deze vergelijking: Turbulentie.
Turbulentie
Kort gezegd is turbulentie het verschijnsel van een instabiele vloeistofstroom. Dit betekent dat een kleine verandering in de vloeistof, veroorzaakt door bijvoorbeeld wrijving (viscositeit), grote gevolgen heeft voor de vloeistofstroom. Een simpel voorbeeld is de rook die van een sigaret afkomt. In eerste instantie gaat de rook recht omhoog en lijkt het alsof naburige rookdeeltjes geen interactie met elkaar hebben. Na ongeveer een centimeter of tien veranderd dit patroon totaal. De naburige rookdeeltjes ‘gaan met elkaar praten’ en veranderen de kalme stroom van rookdeeltjes in een wirwar waarin de rookdeeltjes chaotisch bewegen. Vanuit een theoretische oogpunt is er vanaf dit punt niet veel soeps meer te maken uit de vergelijking van Navier en Stokes.
Dimensie-analyse
Om toch iets te leren over turbulentie, kunnen er een aantal dingen gedaan worden. Ten eerste natuurlijk door experimenten te doen of op een computer de vloeistofstromen te simuleren. Ten tweede kun je door middel van het middelen van de vloeistofsnelheid en dimensie-analyse een hoop te weten komen over turbulentie. Deze laatste optie is erg gemakkelijk en krachtig en geeft je vaak veel inzicht in wat de lengte- en tijdschalen zijn waarop relevante fyscia zich afspeelt. Drie voorbeelden:
1. Grootte. Begin jaren 40 heeft Andrej Kolmogorov bijvoorbeeld laten zien dat het turbulente gebied in een vloeistofstroom groeit als
l ~ constante × t2/7,
waarbij l de grootte is van het turbulente gebied en t de tijd. Naarmate de tijd dus verder gaat, groeit het turbulente gebied. Dit zie je ook bij de rook die van een sigaret afkomt.
2. Snelheid (vroeg). De redenering van Kolmogorov is te ingewikkeld om hier weer te geven, maar een veel simpeler voorbeeld van dimensie-analyse volgt eruit. Stel namelijk dat we nu geïnteresseerd zijn in de snelheid van de vloeistof. Een snelheid is een afstand gedeeld door een tijd. Als we dus weten hoe de karateristieke afstand in de vloestof zich gedraagt, zoals onder (1) hierboven, dan hoeven we die alleen maar door de tijd t te delen om het karakteristieke gedrag van de snelheid te vinden. We vinden dan dus dat de snelheid van de vloeistof afneemt met de tijd, en wel als
v ~ constante / t5/7 .

Afbeelding 2. Andrej Kolmogorov.Bron: Wikipedia. Konrad Jacobs.
3. Snelheid (laat). Het Reynoldsgetal waar we in het vorige artikel over hadden kun je nu met deze informatie uitrekenen – althans: de afhankelijkheid van de tijd. Het resultaat blijkt te zijn dat dit getal afneemt in de tijd, en wel zodanig dat naarmate de tijd verstrijkt, viscositeit belangrijker wordt en er dus meer wrijving optreedt in de vloeistof. Dit heeft dan weer als gevolg dat de snelheid nóg sneller afneemt. Wederom kun je dan via dimensie-analyse laten zien dat de snelheid in het late stadium van turbulentie afneemt met de tijd als
v ~ constante / t5/4 .
Samenvattend: turbulentie is een zeer ingewikkeld verschijnsel waar we slechts een beperkt begrip van hebben. We weten welke tijdschalen en lengteschalen er belangrijk zijn, maar een preciese beschrijving van turubulentie in termen van oplossingen van de Navier-Stokesvergelijking is nog steeds niet bekend. Er zijn de laatste jaren echter heel mooie methoden ontwikkeld die hierop een antwoord zouden kunnen vinden, of op z’n minst een andere blik kunnen werpen op vloeistofmechanica. Wonderlijk genoeg komt dat nieuwe perspectief van een theorie die niks te maken lijkt te hebben met vloeistoffen: snaartheorie. Daarover in een volgend deel van deze serie meer!