
Afbeelding 1. Alles stroomt – maar hoe?Foto: Max Pixel (CC0).
Met behulp van de hydrodynamica kun je voorspellen hoe vloeistoffen stromen. In dit eerste artikel bestuderen we de eenvoudigste eerste stappen die uiteindelijk leiden tot de wetten van de hydrodynamica en de daarbij behorende openstaande problemen.
Een fluïdum
Allereerst een kleine opmerking. Hydrodynamica beschrijft de stroom van een fluïdum. Een fluïdum kan een gas óf een vloeistof zijn. Toch zullen wij hier, een beetje abusievelijk dus, het woord fluïdum consequent vervangen door het woord vloeistof.
Hoe komt het dat fysische systemen met verschillende bouwstenen zich allemaal als vloeistof laten beschrijven? Wanneer we bijvoorbeeld nadenken over de aerodynamica van een auto, dan is het duidelijk dat het ontzettend lastig is om uitsluitend na te denken over allerlei individuele gasdeeltjes die constant tegen elkaar en de auto aan botsen. Sterker nog, het is praktisch onmogelijk om alle gasdeeltjes afzonderlijk te beschouwen.
Vloeistofvolumetjes en stroomlijnen
Het is gemakkelijker om na te denken over vloeistofvolumetjes, die allemaal vergelijkbaar zijn, ontzettend klein, maar wel enorm veel gasdeeltjes bevatten. Het gedrag en de eigenschappen van deze vloeistofvolumetjes (druk, snelheid, dichtheid, enzovoort) wordt beschreven met de wetten van de hydrodynamica. Die wetten van de hydrodynamica voorspellen bepaalde stroomlijnen, zoals te zien is in de afbeelding hieronder.
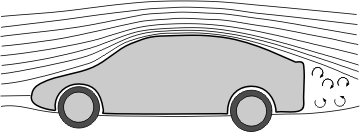
Afbeelding 2. Stroomlijnen rond een auto.Afbeelding: André Huppertz (CC BY-SA 3.0).
Hoe de stroomlijnen lopen, wordt dus bepaald door de wetten van de hydrodynamica. Die wetten hebben allerlei verschillende oplossingen, die verschillende natuurkundige situaties beschrijven. Zoals vaak in de natuurkunde is het goed om eenvoudig te beginnen: we zullen allereerst aannemen dat we wrijving in de vorm van viscositeit (stroperigheid) van de vloeistof kunnen verwaarlozen. Dit stelt ons in staat om de stromingsvergelijkingen te beschrijven.
De wet van Bernoulli
Afbeelding 3 hieronder illustreert een opzet van een experiment waarmee het Venturi-effect gemeten wordt. Dit effect, ontdekt in de 18e eeuw, is het afnemen van de druk van een vloeistof bij het toenemen van de snelheid, bijvoorbeeld doordat de vloeistof door een verdunning in een pijp stoomt.
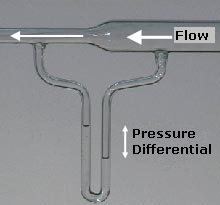
Afbeelding 3. Meten van het Venturi-effect.Afbeelding: Wikipedia-gebruikers ComputerGeezer en Geof (CC BY-SA 3.0).
De wiskundige beschrijving van het verband tussen de druk in een vloeistof en de stroomsnelheid heet de wet van Benoulli. Die wet neemt ook een eventuele verandering mee in de hoogte waarop de vloeistof stroomt. Die hoogte heeft, door de zwaartekracht, effect op de potentiele energie van de vloeistof. De resulterende wet van Bernoulli kan dan eigenlijk ook gezien worden als een precieze beschrijving van het feit dat op een stroomlijn de energie behouden is. Extra aannamen die gedaan moeten worden is dat de vloeistofsnelheid niet fluctueert (je kun Bernoulli alleen toepassen ver genoeg van de ‘trechter’ in het figuur) en dat de vloeistof zogenaamd isentropisch is. Dat laatste komt erop neer dat de temperatuur (of, preciezer: de entropie) niet fluctueert.
De Eulervergelijkingen
De eerste van de twee Eulervergelijkingen kan opgesteld worden met behulp van de tweede wet van Newton: het verband tussen krachten en versnellingen. Het resultaat is is een lastige differentiaalvergelijking die er als volgt uitziet:
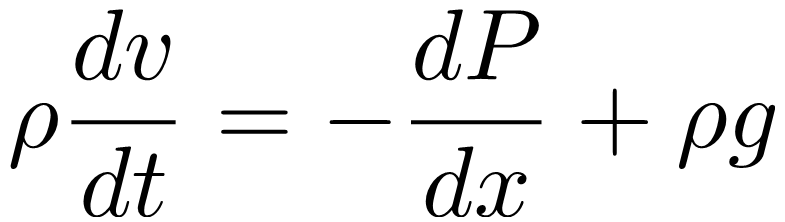
Laten we uitleggen wat hier staat. De ρ staat voor de massadichtheid van de vloeistof, de hoeveelheid massa per kubieke meter op een bepaald punt. De grootheid v is de snelheid van de vloeistof; de afgeleide die in de formule staat is dus de versnelling. P is verder de druk van de vloeistof en g de zwaartekrachtsversnelling. Al deze grootheden zijn in principe afhankelijk van plaats x en het tijdstip t waarop we ze meten. Aan de linkerkant van gelijkteken hierboven staat niets anders dan massadichtheid maal versnelling, een combinatie die zoals gezegd ook in de tweede wet van Newton voorkomt. Aan de rechterkant vind je de resulterende krachtdichtheid, afkomstig van de druk (de eerste term) en van de zwaartekracht (de tweede term).
De tweede Eulervergelijking, die we hier niet in detail zullen uitschrijven, is de continuïteitsvergelijking, die een direct resultaat is van massabehoud. Vaak wordt overigens met de Eulervergelijking alleen de eerste Eulervergelijking aangeduid.
Eulervergelijkingen, Bernoulli en de wetten van Navier-Stokes
De Eulervergelijkingen vormen samen het uitgangspunt waaruit we hydrodynamica of hydrostatica (het gedrag van vloeistoffen die niet stromen) kunnen bedrijven. Willen we weten hoe een vloeistof precies stroomt, dan is onze eerste taak om de Eulervergelijking voor dat specifieke geval goed te begrijpen. Zoals gezegd: hierbij is de belangrijke aanname dat de vloeistof geen wrijving van zichzelf ondervindt.,Wanneer we bovendien eisen dat de vloeistof isentropisch is en de snelheid constant, dan kunnen we uit de Eulervergelijkingen ook de Bernoullivergelijking afleiden.
Wat als we de aanname van wrijvingsloosheid laten vallen? Dan wordt de natuurkunde (en wiskunde) een stuk moeilijker, maar ook een stuk interessanter! Als we wrijving mee zouden nemen, dan moeten we de wetten van Navier-Stokes gebruiken om vloeistoffen te beschrijven – wetten die in de limiet van wrijvingloosheid vereenvoudigen tot de Eulervergelijkingen. Oplossingen voor de Navier-Stokesvergelijking, in de volle algemeenheid, zijn totaal onbekend! Op deze wetten, en de zoektocht naar oplossingen ervan, komen we in de komende artikelen in dit dossier uitgebreid terug.