Hoe complex is de natuur? (1)

Afbeelding 1. De Mandelbrot-set.Complexe getallen zijn niet alleen een heel nuttig rekenhulpmiddel; ze blijken ook een nuttige grafische weergave te hebben. Deze weergave kan bijvoorbeeld gebruikt worden om fractals zoals de beroemde Mandelbrot-set hierboven te contrueren. Afbeelding: Wolfgang Beyer.

Een imaginair getal

Drie maal drie is negen. Min drie maal min drie is ook negen, vanwege de aloude rekenwijsheid ‘min maal min is plus’. Met andere woorden: het kwadraat van een getal is altijd een positief getal, ook als dat getal zelf negatief is.

Het omgekeerde van het kwadraat nemen is worteltrekken. We kunnen de eerste zin uit de bovenstaande alinea ook schrijven als ‘drie is de wortel van negen’. De tweede zin wordt dan ‘min drie is ook de wortel van negen’. Het trekken van een wortel leidt dus tot twee mogelijke uitkomsten: een positieve en een negatieve. De afspraak is meestal om de positieve waarde te kiezen, maar er is helemaal niets mis met de andere keuze.

We kunnen ons nu ook afvragen wat de wortel van min negen is. Het antwoord op die vraag lijkt in eerste instantie niet te bestaan: er is immers geen getal waarvan het kwadraat negatief is. Ook de wortels van min drie, min twaalf of min één lijken dus niet te bestaan.

Wiskundigen houden echter niet van het antwoord ‘bestaat niet’. Op een gegeven moment (of beter: na een lang proces dat al in de 16e eeuw begon) heeft men daarom een oplossing voor dit probleem bedacht. Er werd een nieuw, ‘imaginair’ getal ingevoerd, aangeduid met de letter i (van ‘imaginair’), waarvan werd afgesproken dat het kwadraat -1 is:

i × i = -1

Op het eerste gezicht is dit een nogal abstracte constructie, maar in zekere zin is het niet abstracter dan het gebruik van negatieve getallen zelf. Als ik drie appels heb, en ik neem er vijf weg, hoeveel appels heb ik dan over? Het traditionele antwoord is ‘dat kan niet’, maar het abstracte wiskundige antwoord is ‘min twee’. Als ik de wortel van -1 wil nemen, is het abstracte wiskundige antwoord i.

Afbeelding 2. Gerolamo Cardano (1501-1576).Cardano was in 1545 voor zover bekend de eerste die een rudimentaire versie van complexe getallen gebruikte.

Complexe getallen

Het invoeren van een nieuw wiskundig idee is natuurlijk alleen nuttig als dat idee ook tot nieuwe resultaten en nieuw rekengemak leidt. Voor het imaginaire getal i is dat zeker het geval. Want wat is nu de wortel van -9? Als i × i = -1, dan is 3i × 3i negenmaal zoveel, dus dus -9. (3i is hier de korte schrijfwijze voor ‘driemaal i‘.) We kunnen nu dus niet alleen de wortel van -1 trekken, maar ook van -9, en van elk ander negatief getal!

Het rekengemak houdt daar nog lang niet op. Een slimme lezer zou nu de vraag kunnen stellen: wat is dan de wortel van i, of de wortel van 2i? Moeten we om deze vragen op te kunnen lossen weer een volgend imaginair getal invoeren? Dat blijkt niet zo te zijn. De wortel van 2i blijkt bijvoorbeeld gelijk te zijn aan één plus i. Reken maar na:

(1 + i) × (1 + i) = 1 × 1 + i × 1 + 1 × i + i × i

In deze rekenstap hebben we de haakjes uitgewerkt. Als we nu alle vermenigvuldigingen aan de rechterkant doen, vinden we

(1 + i) × (1 + i) = 1 + i + i – 1

Let op het laatste minteken: i maal i is immers -1! Nu kunnen we alle termen aan de rechterkant optellen, en we vinden inderdaad

(1 + i) × (1 + i) = 2i

Wie van puzzelen houdt, kan laten zien dat (-1 – i) in het kwadraat ook gelijk is aan 2i – ook hier vinden we dus twee mogelijke antwoorden voor de wortel!

Het blijkt dat complexe getallen het mogelijk maken om al dit soort vergelijkingen op te lossen. Ook als we vragen ‘als de zevende macht van een getal plus zijn derde macht gelijk is aan min dertien, wat is het getal dan?’ kunnen we met behulp van complexe getallen een oplossing vinden. Sterker nog: net zoals we voor het vraagstuk van het kwadraat twee oplossingen vonden, vinden we voor dit vraagstuk over een zevende macht maar liefst zeven verschillende oplossingen! Al dergelijke oplossingen zijn van de vorm ‘getal plus getal maal i‘, en dus kunnen we met alleen de bouwstenen ‘getallen’ en ‘getallen maal i‘ al dit soort vergelijkingen oplossen.

Het complexe vlak

We kunnen elk complex getal dus schrijven als x + y i, waarbij x en y gewone (‘reële’) getallen zijn. Dat maakt een eenvoudige grafische weergave van de complexe getallen mogelijk: net zoals we gewone getallen kunnen weergeven op een getallenlijn, kunnen we nu x en y zien als twee coördinaten in een vlak, en complexe getallen dus weergeven als punten in een vlak – zie afbeelding 3.

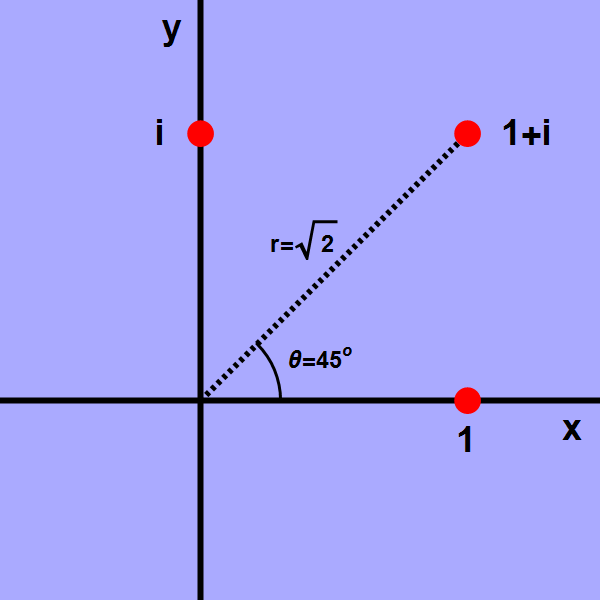
Afbeelding 3. Het complexe vlak.In het complexe vlak tekenen we de gewone (reële) getallen langs de horizontale x-as. De imaginaire getallen zoals i tekenen we langs de verticale y-as. Willekeurige complexe getallen zijn een combinatie van de twee; die geven we weer als punten in het vlak, zoals hier bijvoorbeeld 1+i. Het blijkt erg nuttig om dergelijke punten weer te geven aan de hand van een afstand r en een hoek θ.

Deze grafische weergave blijkt vaak erg nuttig te zijn. Om een voorbeeld te geven (zie wederom afbeelding 3): in plaats van in ‘rechthoekige coördinaten’ x en y kunnen we een complex getal ook aangeven in ‘poolcoördinaten’ – dat wil zeggen: met behulp van de afstand r tot de oorsprong (het getal 0) en een hoek θ. Het vermenigvuldigen van complexe getallen wordt daarmee een stuk eenvoudiger: in plaats van het uitwerken van haakjes, zoals we hierboven deden toen we lieten zien dat het kwadraat van (1+i) gelijk is aan 2i, blijkt het nu mogelijk te zijn om simpelweg de afstanden r van onze twee complexe getallen te vermenigvuldigen, en de hoeken θ op te tellen. Bijvoorbeeld: 1+i heeft afstand √2 (gebruik de stelling van Pythagoras) en een hoek van 45 graden; als we dit getal met zichzelf vermenigvuldigen vinden we dus een getal met afstand √2 × √2 = 2 en hoek 45 + 45 = 90 graden, dus inderdaad 2i!

Rekenen met complexe getallen is leuke hersengymnastiek. Wie meer wil weten kan online heel veel informatie vinden; een mooi startpunt is bijvoorbeeld de tutorial van Math is Fun.

Complexe getallen in de natuur

Er bestaat een beroemd artikel van de natuurkundige Eugene Wigner met de titel ‘The unreasonable effectiveness of mathematics in the natural sciences’. De ‘onredelijke effectiviteit’ van de wiskunde in de natuurkunde is inderdaad opvallend: wiskundigen kunnen het zo gek niet bedenken, of hun constructies hebben wel ergens in de natuurkunde een toepassing.

Geldt dat ook voor complexe getallen? Trekt de natuur ook wortels uit negatieve getallen? Jazeker! Er bestaat zelfs een overvloed van toepassingen van de complexe getallen in de natuurkunde. In het tweede deel van dit drieluik zullen we een aantal van deze verrassende toepassingen bespreken.