Hoe complex is de natuur? (3)

Afbeelding 1. Een quantumdeeltje.Een quantumdeeltje heeft zowel eigenschappen van een deeltje, als van een golf. Artist impression van Stef Simmons (UCL).

Quantumfysica en complexe getallen

Zoals we in het vorige artikel hebben gezien, zijn complexe getallen erg nuttig in het beschrijven van allerlei golfverschijnselen: licht, wisselstroom, enzovoort. De meest voorkomende golf, een sinusvormige golf, kunnen we heel eenvoudig beschrijven als component van een complexe machtsfunctie. Daarmee lijkt het voor de hand te liggen dat ook in de quantummechanica complexe getallen een rol spelen. Een heel belangrijk resultaat van die theorie is immers dat elementaire deeltjes ook als golven beschreven kunnen worden, en omgekeerd – de beruchte golf-deeltjedualiteit. Een quantummechanisch elektron (of een willekeurig ander elementair deeltje) is geen puntvormig kogeltje, maar een klein, gelocaliseerd golfje – en dus lijkt een bechrijving met behulp van complexe getallen een goed idee.

Bij het ontwikkelen van de grondbeginselen van de quantumfysica, grofweg een eeuw geleden, beek dit “goede idee” zelfs uitmuntend te zijn. Niet alleen is het gemakkelijk om quantumgolven als complexe golven te beschrijven; allerlei elementen uit het rekenen met complexe getallen blijken dan ook een zeer fysische interpretatie te krijgen. We hebben in het eerste artikel gezien dat we complexe getallen op twee manieren kunnen beschrijven (zie afbeelding 2): aan de hand van een reële component x en een imaginaire component y, of aan de hand van een hoek θ en een afstand r. De eerste beschrijving is heel nuttig als we sinusvormige golven willen weergeven, maar ook de hoek en de afstand spelen in de quantummechanica een belangrijke rol.

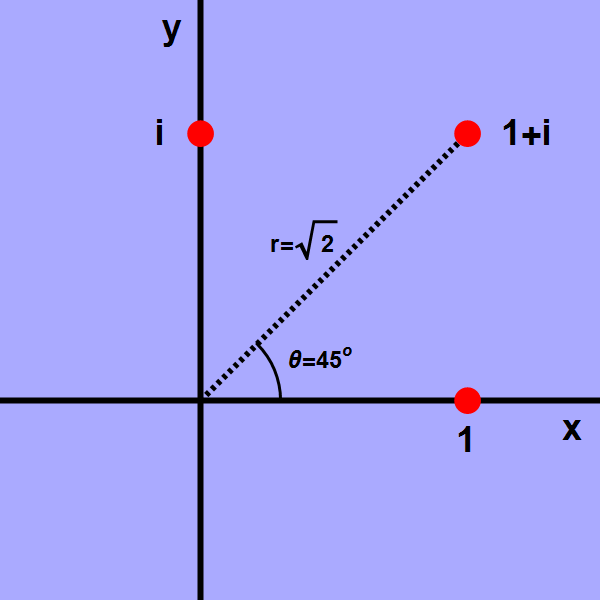
Afbeelding 2. Complexe getallen.We kunnen complexe getallen op twee manieren beschrijven: aan de hand van een reëel deel x en een imaginair deel y, of aan de hand van een afstand r en een hoek θ.

Complexe afstanden en quantumkansen

Laten we met de afstand beginnen. Wat beschrijft een quantumgolf eigenlijk? Uit het werk van Max Born en vele anderen weten we het antwoord: quantummechanica maakt deeltjes “fuzzy”. Net als een golf op het water heeft ook een quantumdeeltje geen heel nauweurig bepaalde plaats. We moeten daarom niet spreken van de exacte locatie van een deeltje, maar van de kans om een deeltje ergens aan te treffen. Is de quantumgolf ergens hoog, dan is de kans om het deeltje daar te vinden groot; is de golf laag, dan is die kans klein. Het precieze wiskundige recept blijkt als volgt te zijn: de kans om een deeltje ergens aan te treffen, is evenredig met het kwadraat van de afstand r van de complexe kansgolf tot het getal nul.

Overigens is dit “kwadraat van de afstand” een grootheid die met complexe getallen heel makkelijk uit te rekenen is. Neem een willekeurig complex getal, bijvoorbeeld

2+3i

Neem vervolgens de zogeheten “complex geconjungeerde” van dit getal: hetzelfde getal, maar met een minteken voor het imaginaire deel. In dit voorbeeld is de complex geconjungeerde dus

2-3i

Vermenigvuldig vervolgens deze getallen. We vinden als we de haakjes wegwerken dat alle imaginaire getallen wegvallen en dat we een normaal, reëel getal overhouden:

(2+3i) × (2-3i) = 4 – 6i + 6i + 9 = 13

waar we in de eerste stap gebruikt hebben dat i×i=-1. Merk op dat het antwoord ook geschreven kan worden als

2²+3²

dus we vinden de som van de kwadraten van de twee componenten van 2+3i. Met andere woorden: hier staat volgens de beroemde stelling van Pythagoras niets anders dan het kwadraat van de afstand van 2+3i tot 0!

De wijze les van dit verhaal (die algemeen blijkt te gelden) is daarmee: kansen in de quantummechanica vinden we door quantumgolven met hun complex geconjungeerde te vermenigvuldigen.

Complexe hoeken en quantumsuperpositie

Hoe zit het met de hoek θ van de complexe quantumgolf? Aangezien de kans om een deeltje ergens aan te treffen alleen afhangt van de afstand r, zouden we verwachten dat die hoek θ geen waarneembare grootheid is. De kansen veranderen immers niet als we θ veranderen. Voor een enkele quantumgolf blijkt dit inderdaad het geval te zijn: de hoek van zo’n golf kunnen we in een experiment nooit meten.

Dat betekent echter niet dat het bestaan van die hoek geen fysische impact heeft! Net als watergolven hebben quantumgolven namelijk de eigenschap dat ze interferentie kunnen vertonen: als twee watergolven elkaar passeren, kunnen ze elkaar versterken (als beide golven op een top of beide in een dal zijn) of juist uitdoven (als één golf op een top is, en de andere in een dal). Zie afbeelding 3 voor een voorbeeld.

Afbeelding 3. Interferentie van watergolven.Waar twee golven allebei een top of allebei een dal hebben, versterken ze elkaar. Waar één golf een top en de andere een dal heeft, doven de golven elkaar uit. Het gevolg is het ‘ruitjespatroon’ dat we hierboven zien in het gebied waar de golven elkaar tegenkomen.

Hoe zit dat met quantumgolven? Ook die kunnen interferentie vertonen, maar nu complexe interferentie. Ook twee quantumgolven die hetzelfde systeem beschrijven `tellen bij elkaar op’, net als dat voor watergolven gebeurt. We noemen dit optelverschijnsel de superpositie van quantumtoestanden. Als de twee hoeken θ voor de twee golven hetzelfde zijn, versterken ze elkaar; als de twee hoeken precies tegengesteld zijn, doven de twee golven elkaar uit, en voor alle hoeken daartussenin is er sprake van gedeeltelijke versterking of uitdoving.

Dit verschijnsel zien we heel mooi in het beroemde tweespletenexperiment: wanneer we losse elektronen (of andere deeltjes) op een scherm afsturen waarin zich twee spleten bevinden, gaan de quantumgolven door beide spleten heen, en komen die golven op een tweede scherm achter de spleten weer bij elkaar. Daarbij kunnen de golven elkaar zoals hierboven beschreven versterken of verzwakken, en dus ontstaan er gebieden waar de kans om het deeltje aan te treffen heel groot is, en gebieden waar die kans juist heel klein is. Doen we dit experiment voor een groot aantal deeltjes (afbeelding 4) dan zien we de kansverdeling, met de pieken en dalen daarin, heel mooi verschijnen.

Afbeelding 4. Interferentie van elektronen.Losse elektronen (a) komen op het scherm achter de twee spleten aan, en zijn daar te zien als een witte stip. Als we het experiment heel vaak herhalen (e) is duidelijk een interferentiepatroon van lichte en donkere banden te zien. Afbeelding: A. Tanamura.

Hoe complex is de natuur?

Kortom: complexe getallen zijn ideaal geschikt om quantumgolven te beschrijven. Niet alleen zijn vlakke golven gemakkelijk met behulp van zulke getallen te vormen; bovendien spelen in het berekenen van quantumkansen en quantumsuperposities de afstand r en de hoek θ een cruciale rol.

Kunnen we daarmee dus stellen dat de natuur ‘uit complexe getallen bestaat’? Die vraag is eigenlijk meer een filosofische dan een natuurkundige. We kunnen elk complex getal immers zien als een tweetal gewone, reële getallen: het getal 2+3i kunnen we natuurlijk ook weergeven als het coördinatenpaar (2,3). Elke berekening die we met complexe getallen kunnen doen, kunnen we vervolgens herschrijven als een berekening met zulke paren, en dus hebben we strikt genomen complexe getallen nooit nodig.

Aan de andere kant wordt het rekenwerk met behulp van complexe getallen zoveel eenvoudiger en eleganter dat het werken met paren van getallen uiteindelijk wel erg omslachtig is. De taal van de natuur is het mooist als we die in complexe getallen uitschrijven. Of de natuur dus complex is, is misschien wel een kwestie van smaak, maar laten we het erop houden dan de natuur zich bijzonder complex voordoet!