Grip op oneindig

De theoretische natuurkunde is overladen met ingewikkelde modellen waarin het verkrijgen van exacte antwoorden bijna ondoenlijk is. Zoals eerder uitgelicht maken fysici daarom graag gebruik van storingsrekening. De filosofie achter deze methode is het idee dat we een parameter \( g \) – ook wel de koppeling genoemd – in ons model introduceren. Die koppeling interpoleert tussen een simpel behapbaar model (met \( g = 0 \)) dat we makkelijk kunnen oplossen, en een meer complex model (met \( g \neq 0\)) waar we daadwerkelijk in geïnteresseerd zijn. Door aan te nemen dat de koppeling g zeer zwak is – dat wil zeggen dat \( g \) veel kleiner is dan één – kunnen we toch berekeningen doen in het complexe model. De antwoorden die we vinden zijn dan machtreeksen in g de we kunnen interpreteren als correcties op de oplossing van het originele simpele model.

Dit alles zal misschien een beetje abstract klinken. Laten we daarom eens een voorbeeld uit de natuurkunde nemen om deze methode op toe te passen. Het voorbeeld dat we bekijken komt uit de quantumveldentheorie en heet het \( \phi^3 \)-model dat een zeer bekend toy model is uit de studie van zulke theorieën.

Interacties, diagrammen en reeksen

We beginnen met een simpeler model dat we een vrije veldentheorie noemen. Deze theorie noemen we ‘vrij’ omdat die zo simpel is dat er geen interacties zijn, wat betekent dat er geen wisselwerking tussen de deeltjes is en ze dus vrij langs elkaar heen bewegen. Dit model is zo makkelijk dat we de meeste vragen die je erover kan stellen makkelijk kunnen beantwoorden. Omdat er geen interacties zijn, kunnen we voor dit model geen interessante diagrammen tekenen die de interacties weergeven (de zogeheten feynmandiagrammen): de enige diagrammen zijn simpelweg rechte lijnen.

In de echte wereld zijn er echter wél interacties tussen deeltjes, en dus willen we deze toevoegen aan ons model. Het vrije model plus interacties wordt het meer gecompliceerde model waar we in geïnteresseerd zijn. Zoals storingsrekening ons leert, moeten we deze interacties toevoegen met een koppeling \( g \), die ons laat interpoleren tussen het model zonder (\( g = 0 \)) en mét (\( g \neq 0 \)) interacties. Schematisch kunnen we dit als volgt weergeven:

\( \mathcal{L}_{\text{nieuw}} = \mathcal{L}_{\text{vrij}} + g \cdot \phi^3 \).

De eerste term aan de rechterzijde belichaamt de vrije theorie die we volledig begrijpen. De tweede term is het extra ingrediënt dat we toevoegen: we noemen dit een kubische interactie, ook wel een driepuntsinteractie. Deze naam komt van het getal drie dat je in de macht van de \( \phi \) ziet. De wiskunde vertelt ons nu dat we feynmandiagrammen mogen tekenen waarin steeds drie lijnen samen komen in één punt, ook wel een vertex genoemd (meervoud vertices); in die vertices valt een deeltje uiteen in twee andere deeltjes of botsen twee deeltjes juist en vormen ze een nieuw deeltje. Voorbeelden van diagrammen die we nu dus kunnen tegenkomen zijn:

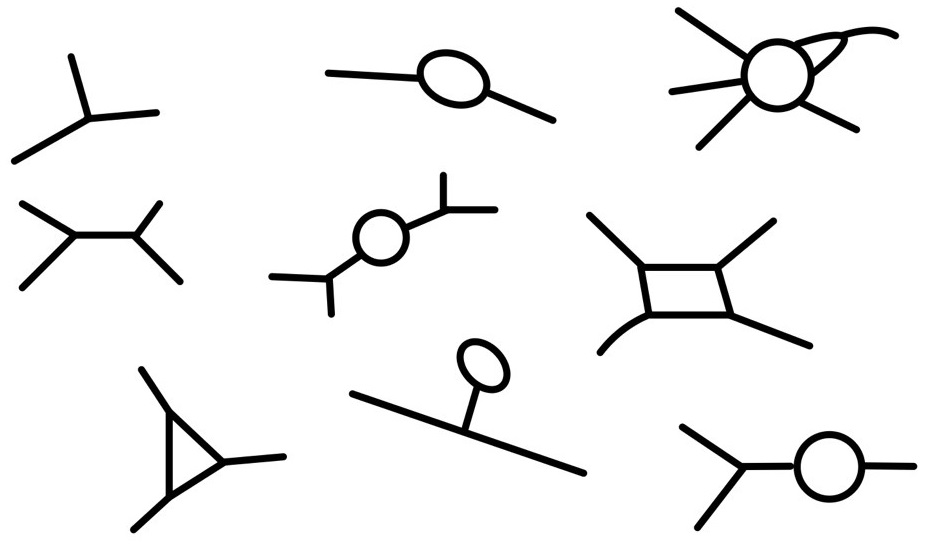
De koppeling \( g \) die in de rechter term van de vergelijking hierboven staat, geeft dus zoals gezegd de kracht of intensiteit van de interactie weer. In essentie zijn feynmandiagrammen representaties van berekeningen die je uiteindelijk een getal geven; een getal dat je iets vertelt over de kans waarmee de verschillende processen gebeuren. Als we in ons nieuwe verstoorde model een interessant proces willen bestuderen zullen we de berekeningen waarin deze feynmandiagrammen tevoorschijn komen moeten doen. Laten we kijken naar een proces waarin we twee deeltjes op elkaar af sturen en er uiteindelijk ook weer twee deeltjes uit komen. We noemen dit ook wel een verstrooiingsproces. De relevante feynmandiagrammen moeten in dit geval vier externe benen hebben: twee voor de inkomende deeltjes en twee voor de uitgaande deeltjes. De volgende diagrammen kunnen we dan associëren met dit proces:

Wat zien we hier? Het eerste diagram toont ons simpelweg twee deeltjes die langs elkaar bewegen zoals we in het originele vrije model zouden verwachten. Dat is echter niet het enige dat nu kan gebeuren. Het tweede diagram laat zien dat het ook mogelijk is dat de twee deeltjes samenkomen en een nieuw deeltje vormen dat daarna weer vervalt in twee. Daarnaast kunnen we nog gecompliceerde situaties schetsen zoals je in het derde tot en met het zesde diagram kunt zien. Er zijn nog veel meer diagrammen mogelijk, te veel om hier allemaal te tekenen. Het interessante nu is dat quantummechanica ons vertelt dat, als we het verstrooiingsproces van twee inkomende en twee uitgaande deeltjes willen begrijpen, we rekening moeten houden met alle mogelijke diagrammen die we maar kunnen tekenen! Dat zijn in dit geval dus alle diagrammen met driepuntsvertices en vier externe benen.

Dit leidt tot het volgende evidente probleem: er zijn oneindig veel van zulke diagrammen. Ook een diagram met zes ‘lussen’ zou moeten bijdragen aan ons verstrooiingsproces. Hoe krijgen we grip op deze overvloed aan mogelijkheden? En als we als we oneindig veel bijdragen (lees: diagrammen) bij elkaar moeten optellen, krijgen we dan niet iets oneindig groots?

Dit is waar storingsrekening ons uit de brand gaat helpen. Zoals eerder genoemd draagt de driepuntsinteractie een parameter \( g \) die de intensiteit bepaalt. Een van de regels van feynmandiagrammen (ook wel feynmanregels genoemd) vertelt ons dat iedere vertex een factor \( g \) oplevert in de bijdrage van het diagram aan het eindantwoord. Deze bijdrage is multiplicatief: dat betekent dat \( n \) vertices een factor \( g^n \) bijdragen. Het eerste wat dus kunnen doen is alle diagrammen ordenen op het aantal vertices dat ze hebben:

De daadwerkelijk bijdrage van de diagrammen volgt uit een ingewikkelde berekening die we hier niet zullen toelichten – de uitkomst van die berekeningen is hierboven aangegeven door de variabelen \( a, b \) en \( c_i \) – maar het uiteindelijke resultaat zal hoe dan ook schalen met een zekere macht van \( g \).

Nu komt een belangrijke observatie: Als we aannemen dat de koppeling \( g \) veel kleiner dan één is (dat noemen we zwakke koppeling) dan zien we dat het eerste diagram veel sterker bijdraagt dan het tweede, en het tweede weer sterker dan het derde, vierde, vijfde en zesde. Dit komt doordat het product van twee getallen die kleiner dan één zijn, altijd weer kleiner is de originele twee getallen¹. Alle diagrammen die we niet getekend hebben kunnen we ordenen op het aantal vertices dat erin voorkomt, en hoewel we ze niet allemaal kennen kunnen we garanderen dat ze meer vertices hebben, dus met een hogere macht van \( g \) schalen, en dus veel zwakker zijn². Wat we dus hier in essentie hebben is een machtreeks!

We zeggen dus dat dit model een lichte verstoring is boven op onze oorspronkelijke vrije theorie. Eerder merkten we al op dat, als de koppeling op nul wordt gezet, we de vrije theorie weer terugvinden. Dat zien we ook terug in de diagrammen: zodra we \( g = 0 \) kiezen blijft alleen het eerste diagram, waarin geen interactie plaatsvindt, over – zoals verwacht. Als je nu wil weten wat de totale intensiteit \( A \) van dit verstrooiingsproces is, moet je alle bijdragen bij elkaar optellen, en krijg je zoals gezegd de machtreeks

\( A = a + b g^2 + \left(c_1+c_2+c_3+c_4\right)g^4+ \mathcal{O}(g^6) \).

\( A \) vertelt je zoals gezegd iets over de kans waarmee het totale verstrooiingsproces plaatsvindt. Het laatste symbool rechts noemt men ook wel de grote O notatie: die zegt dat verdere contributies schalen met \( g^6 \) of hogere machten, en dus volgens onze logica heel erg klein zijn. Als we nu voor een gegeven (kleine) \( g \) de waarde van deze reeks willen uitrekenen kunnen we dus één voor één diagrammen tekenen, de bijbehorende coëfficiënten uitrekenen en bij elkaar optellen. Als we de gewenste precisie hebben bereikt kappen we de serie af en hebben we ons resultaat (tot op zekere hoogte) gevonden. Een nog preciezer antwoord kan altijd bereikt worden – zo lijkt het in elk geval – door nog een extra orde toe te voegen en te berekenen.

Divergerende reeksen

Wat we gezien hebben is dat – hoewel er voor een gegeven verstrooiingsproces oneindig veel diagrammen zijn – we deze diagrammen kunnen sorteren aan de hand van het aantal vertices en zo systematisch de berekening kunnen uitvoeren tot op arbitraire precisie. Één impliciete aanname die echter in dit verhaal schuilt, is dat de waardes \( a, b, c, d \ldots \) niet sneller groeien dan de reeks \( 1, g^2, g^4, g^6, \ldots \) krimpt. Als dit wel zo is, dan hebben we te maken met een divergente reeks. Een voorbeeld van een divergerende reeks is

\( A = \sum_{n=0}^\infty (n!) g^n \).

Hierin is \( n! \) de faculteitsfunctie, dus bijvoorbeeld \( 5! = 5 \times 4 \times 3 \times 2 \times 1 \). Ongeacht hoe klein we \( g \) kiezen, op een zeker moment zal de coëfficiënt \( n! \) harder groeien dan \( g^n \) krimpt. Dit kun je zien door het feit dat als we van macht \( n \) naar macht \( n+1 \) gaan, de bijdrage van \( n!g^n \) naar \( (n+1)!g^{n+1} \) gaat, wat dus een factor \( (n+1)g \) verschil oplevert. Op een zeker moment komen we op het punt aan dat \( n+1 \) groter is dan \( 1/g \) (zodat dus \( (n+1)g > 1 \)) en de volgende term groter wordt. Ook de daaropvolgende contributies worden niet langer kleiner, maar juist groter! Dit is al eerder toegelicht in dit artikel op onze website.

Is onze reeks van feynmandiagrammen ook een divergerende reeks? Het antwoord is ja. Dit werd al lang geleden beargumenteert door Freeman Dyson voor het geval van quantumelektrodynamica, de theorie van elektronen en hun elektrische krachten, maar het gaat ook op voor ons \( \phi^3 \)-model. De reden dat de coefficiënten \( a, b, c, \ldots \) zo hard groeien is niet dat de contributies van de hogere order diagrammen zelf zo groot zijn, maar dat het aantal diagrammen dat voor iedere macht \( g^n \) verschijnt zoals we gezien hebben extreem hard groeit. Denk maar na over hoeveel diagrammen er bij orde \( g^6 \) zullen verschijnen; deze QU redacteur durft wel te gokken dat het er minstens twintig zullen zijn. Het verschijnsel dat het aantal diagrammen zo hard groeit en leidt tot een divergerende reeks schrijven natuurkundigen toe aan de aanwezigheid van zogenaamde instantonen. Dit begrip – dat al eerder voorbijkwam in dit artikel – duidt op het feit dat er natuurkundige effecten in ons model plaatsvinden (zoals het tunnelen van quantumdeeltjes) die we niet met een gewone machtreeks zoals hierboven gegeven kunnen beschrijven. Doordat de machtreeks die je wilt uitrekenen divergeert vertelt de theorie je zo als het ware dat je beschrijving van het model niet compleet is.

Naast dit instantoneffect bestaat er in sommige quantumveldentheorieën ook nog een vergelijkbaar effect dat we toeschrijven aan zogenaamde renormalonen. Dit effect werd in de jaren 70 al werd ontdekt door onder anderen de Nederlandse Nobelprijswinnaar Gerard ’t Hooft en recent is er hernieuwd interesse ontstaan in het begrijpen van dit mysterieuze renormalonverschijnsel. Wat een renormalon is en hoe het zijn vingerafdrukken achterlaat in machtreeksen zoals die hierboven, zal ik bespreken in een toekomstig artikel!

[1] In dit geval hebben we dus \( 1 > g^2 > g^4 > g^6 > \ldots \) enzovoort.

[2] De kritische QU-lezer zal opmerken dat ver uiteenlopende waardes van \( a, b \) en \( c \) deze rangschikking ongeldig kunnen maken, maar de logica werkt ook omgekeerd: gegeven de waarden van \( a, b \) en \( c \) kunnen we altijd een waarde vinden voor \( g \) zodat deze rangschikking toch werkt.