De onontkoombaarheid van het oneindige

In een eerder artikel¹ zagen we dat natuurkundigen berekeningen in quantumveldentheorie doen door voor een specifiek proces – zoals de botsing van twee deeltjes – Feynmandiagrammen te tekenen en deze te rangschikken aan de hand van het aantal zogenaamde vertices. Deze rangschikking stelt ons in staat om orde te scheppen in de oneindige verzameling van mogelijke diagrammen en effectief de gewenste berekening uit te voeren. Het resultaat is een machtreeks, een optelsom met oneindig veel bijdragen waarvan het resultaat het uiteindelijke antwoord geeft waar we naar zoeken. Wat we in dat artikel echter ook opmerkten, is het feit dat deze reeksen in de quantumveldentheorie meestal divergeren: na een zeker moment wordt elke volgende term groter en groter².

Hoe weten we zo zeker dat die bewering waar is? Is het echt zo dat de meeste machtreeksen die te vinden zijn in quantumveldentheorieën oneindig groot worden? Die vraag gaan we in dit artikel proberen te beantwoorden.

Het Dyson-argument

De bekende natuurkundige Freeman Dyson was een van de eersten die opmerkte dat getallenreeksen in de quantumveldentheorie zouden moeten divergeren. Hij beargumenteerde dit in het specifieke geval van quantumelektrodynamica – de quantumveldentheorie die elektriciteit en magnetisme beschrijft – maar het argument is breder toepasbaar. Laten we eens kijken naar wat Dyson in zijn artikel precies zegt.

De theorie van quantumelektrodynamica beschrijft hoe geladen deeltjes elkaar aantrekken of afstoten. Net als andere quantummodellen kent de theorie een koppelingsconstante die de intensiteit van interacties beschrijft. Een handige formulering is in termen van het kwadraat van de elektronlading, \( e^2 \), omdat dat kwadraat bijvoorbeeld de kracht beschrijft waarmee twee elektronen elkaar afstoten. Als we net als in het vorige artikel een proces willen bestuderen, volgen we weer onze standaardprocedure van Feynmandiagrammen uittekenen, rangschikken op het aantal vertices en vervolgens optellen. Dit leidt tot een getallenreeks die we symbolisch kunnen schrijven als

\( F(e^2) = a_0 + a_2 e^2 + a_4 e^4 + \mathcal{O}(e^6) \).

Hierin is \( \mathcal{O} \) de notatie die ons vertelt dat er nog meer termen zijn die van orde \( e^6 \) of hoger zijn. Wat Dyson wilde beargumenteren is het volgende: de getallenreeks F móét wel divergeren, omdat het alternatief – een convergerende reeks – leidt tot een model voor elektromagnetisme dat bepaalde bekende eigenschappen niet heeft waardoor je onmogelijk de coëfficiënten \(a_i \) kan reproduceren. Het type argument dat Dyson wil toepassen is een bewijs uit het ongerijmde (‘reductio ad absurdum’): we nemen aan dat onze stelling – dat F divergeert – juist níét waar is, en laten zien dat dat leidt tot een tegenstelling.

Het eerste dat we moeten begrijpen is wat het voor onze getallenreeks betekent als hij niet divergeert. In dat geval hebben we dus te maken met een convergerende reeks, waarvan de uitkomst afhankelijk is van de waarde van de koppeling \(e^2\). Iets preciezer: of de reeks wél of níét convergeert kan nog van de waarde van \(e^2\) afhangen. Wiskundigen vertellen ons dat er voor een reeks die niet divergeert, een waarde \(e_0\) moet zijn, zodat de reeks \(F(e^2) \) convergeert wanneer

\( | e^2 | \leq e_0^2 \).

Merk op dat er aan de linkerkant van de vergelijking absolute-waardestrepen staan. Maar… \( e^2 \) is, als kwadraat, toch altijd positief? Dat is waar, maar Dysons argument gaat juist over de vraag wat er zou gebeuren als er op de plaats van \( e^2 \) in de berekeningen een negatief getal zou komen te staan. De wiskunde vertelt ons dat, als die negatieve waarde maar klein genoeg is, de reeks nog steeds zou moeten convergeren.

Het tweede wiskundige feit dat we nodig hebben is dat, als we ons beperken tot waarden voor \(e^2\) die aan de hierboven staande ongelijkheid voldoen, we de reeks F kunnen interpreteren als een analytische functie die goed gedefinieerd is voor alle waarden van \(e^2\) die aan deze ongelijkheid voldoen. Dit betekent in het bijzonder dat we de waarde van \(e^2\) heel langzaamaan kunnen veranderen – eventueel dus ook naar negatieve waarden – waarbij F ook maar langzaam verandert.

Nu komt een belangrijke stap in argumentatie van Dyson: we verwachten op basis van de bovenstaande redenering dat elektrodynamica een wiskundig consistent model is dat werkt ongeacht de waarde van \( e^2 \). Als \( F(e^2) \) echt een analytische functie is, dan moet de functie ook werken voor negatieve waarden van \( e^2 \). Stel nu dat we in een denkbeeldig universum zouden leven waarin \( e^2 \) inderdaad niet positief maar negatief is, hoe zou de wereld er dan uitzien?

Een fictief universum

Een van de wetten van de elektrodynamica is dat de kracht tussen twee ladingen bepaald wordt door de formule³

\( F_{\text{EM}} \simeq \frac{q_1 q_2 e^2}{r^2} \).

Hier staan \( q_1 \) en \( q_2 \) voor twee ladingen die door middel van elektromagnetische interactie op elkaar werken, en de variabele \( r \) is de afstand tussen de twee. In het geval dat de twee ladingen tegengesteld zijn (één positieve en één negatieve) hebben we

\( q_1 = -q_2 = q \qquad \) en dus \( \qquad F_{\text{EM}} < 0 \)

Dit bekent dat de kracht F die op de ladingen werkt aantrekkend is. Stel nu dat we naar ons fictieve universum gaan waar \(e^2\) juist een negatieve waarde heeft. Dan belanden we bij de tegenovergestelde conclusie, namelijk dat daar de kracht tussen een negatieve en positieve lading afstotend is.

Een ander interessant verschijnsel in de quantumveldentheorie is het vacuüm. In het dagelijks leven denken we bij een vacuüm aan een compleet lege ruimte, vrij van enig deeltje of wat dan ook, maar in de quantummechanica zit dit concept net iets anders in elkaar. Daarin spreken we van een vacuümtoestand, wat betekent: de toestand met de laagste energie. Omdat quantummechanische systemen hun energie altijd willen verlagen, zal een systeem altijd proberen zijn energie kwijt te raken om zo terug te vallen in zijn vacuümtoestand. Dit kan uiteraard alleen als er een vacuüm bestaat, ofwel: als alle mogelijke energietoestanden een ondergrens hebben.

Je zou verwachten dat ook zo’n vacuüm leeg is, maar dit blijkt niet helemaal waar te zijn. Als je heel nauwkeurig zou meten zou je zien dat er in het vacuüm een enorme soep is van deeltjes die spontaan uit het niets ontstaan en in een fractie van een seconde weer verdwijnen. Hoe is dat mogelijk? Om dat te begrijpen hebben we twee belangrijke natuurwetten nodig. De eerste komt uit de speciale relativiteitstheorie van Einstein, en vertelt ons dat we uit energie massa kunnen maken en vice versa. De tweede wet die we nodig hebben komt uit de quantummechanica en is een gevolg van Heisenbergs onzekerheidsrelatie voor de energie:

\( \Delta E \Delta t \geq \frac{\hbar}{2} \).

Deze vergelijking vertelt ons grofweg dat, als we de energie in een tijdsinterval \( \Delta t \) meten, er altijd een onzekerheid \( \Delta E \) zit in de gemeten energie, en dat die onzekerheid een bepaalde minimale waarde heeft. Deze onzekerheid blijkt zelfs in het vacuüm te zitten: in eenzelfde tijdsinterval \( \Delta t \) kan daarom bijvoorbeeld een hoeveelheid energie ter grootte van \( \Delta E \) omgezet worden in twee deeltjes. Dit zouden een elektron en een positron kunnen zijn, zodat de totale lading \( +1 – 1 = 0 \) behouden blijft. De twee deeltjes verschijnen kort vanuit het vacuüm, maar vallen door de aantrekkende kracht die ze op elkaar uitoefenen weer terug en vernietigen elkaar. Dit mag allemaal gebeuren volgens de wetten van de quantummechanica, zolang het maar binnen het tijdsbestek \( \Delta t \) gebeurt. De conclusie: een quantumvacuüm is niet leeg, maar wel stabiel. Deeltjes kunnen uit het niets ontstaan, maar ze leven maar heel kort en verdwijnen altijd weer.

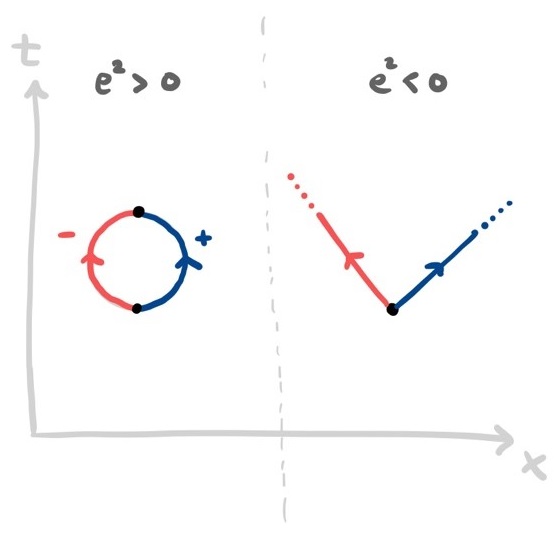
Laten we nu weer teruggaan naar ons fictieve universum gaan. Ook daar gelden de wetten van de quantummechanica en is een vacuüm dus niet echt leeg. Wat we nu echter waarnemen is dat de elektronen en positronen die in het vacuüm ontstaan elkaar afstoten. Dat betekent dat de ontstane deeltjes niet terug op elkaar vallen, maar juist in een hoog tempo uit elkaar gedreven worden.

Dit leidt tot een catastrofale situatie. Uit het niets ontstaat een eindeloze stroom deeltjes, die langzaamaan het hele universum vullen. We concluderen dat het vacuüm niet langer stabiel is: zodra een deeltjespaar ontstaat, verliest het vacuüm een beetje energie, die het daarna in de ‘gewone’ wereld weer terug zou krijgen als de deeltjes weer verdwijnen. In ons fictieve universum gebeurt dat laatste echter niet, en dus neemt de energie van het vacuüm langzaam af.  Onze fictieve wereld kent geen stabiele grondtoestand (geen ‘echt’ vacuüm), en in zo’n universum houdt onze functie F – die iets vertelt over deeltjesprocessen in het vacuüm – op te bestaan! Het is onmogelijk[4] om in het fictieve universum met dezelfde functie \( F(e^2) \) processen te beschrijven. Dyson trok daaruit de conclusie dat F geen analytische functie kan zijn, en dat daarom de aanname dat de machtreeks convergeert nooit juist kon zijn geweest. Het naief optellen van alle termen moet, zelfs voor positieve \( e^2 \), dus oneindig opleveren!

Het is belangrijk om in het achterhoofd te houden dat het bovenstaande slechts en heuristisch argument is en absoluut geen volledig wiskundig bewijs. De redenering klinkt echter zeer aannemelijk, kan ook op andere manieren met berekeningen ondersteund worden, en lijkt ook toepasbaar op een brede klasse van andere modellen. Een voorbeeld is de anharmonische oscillator, een eenvoudig quantumsysteem waarvoor de natuurkundigen Carl Bender en Tai Tsun Wu in de jaren 60 al aantoonden dat de machtreeks voor grondtoestand van de energie divergeert. De anharmonische oscillator is een model van één deeltje met positie x waarvan de potentiële energie V(x) van de positie afhangt als

\( V(x) =  x^2+g x^4 \).

In deze uitdrukking speelt de parameter g weer de rol van een koppelingsconstante. Net als in quantumveldenheorie kunnen we een simpeler model, dat met \( g=0 \), exact oplossen – dit eenvoudigere model staat bekend als de quantum-harmonische oscillator – en vervolgens kunnen we de ‘anharmonische term’ \( gx^4 \) toevoegen als een storing. Als we dan de energie van de grondtoestand in dit model willen berekenen, vinden we een machtreeks van de vorm

\( E(g) = E_0 + E_1 g + E_2 g^2 + E_3 g^3 + \mathcal{O}(g^4) \).

Bender en Wu berekenden een enorm aantal van de coëfficiënten \( E_i \) en konden zo laten zien dat de reeks inderdaad divergeerde. Ook hier kunnen we Dysons argument gebruiken: indien de reeks convergerende zou zijn geweest, hadden we ook kunnen kijken naar wat er gebeurt als g negatief is. Als je de functie V(x) tekent voor verschillende waarden van g, zoals in figuur 2, zie je dat de functie dan abrupt verandert. We vinden zodra het teken van g verandert een potentiële-energiefunctie waarin een deeltje niet langer onherroepelijk vast blijft hangen in het midden, maar door middel van quantummechanisch tunnelen kan ontsnappen waarna de energie vrij naar beneden kan afglijden.

Een deeltje dat op zo’n manier kan ontsnappen, heeft geen grondtoestand en dus kan de hierboven gegeven uitdrukking \( E(g) \) niet langer tot een eindig resultaat leiden. We concluderen wederom dat het om een divergente reeks moet gaan, net zoals Dyson dat deed voor de quantumelektrodynamica.

We hebben dus gezien dat Dysons argument, hoewel heuristisch, zeker hout snijdt. Betekent dat dus dat de natuurkunde faalt, nu al deze reeksen naar oneindig lijken te gaan? Zeker niet! Hoewel de naieve optelsommen het antwoord ‘oneindig’ lijken te geven, verwachten we nog steeds dat ze ons iets vertellen over de natuur. In die zin is het divergeren een mooi gegeven: we leren eruit dat we kennelijk nog extra informatie missen, waaruit we kunnen leren hoe we wél een eindig, fysisch antwoord uit dergelijke berekeningen kunnen halen. Divergerende reeksen blijken ons zo te wijzen op allerlei interessante fenomenen, zogeheten instantonen en andere bijzondere effecten. Als je daar meer over wilt weten raden we je aan deze serie artikelen over storingsrekening in de toekomst nog eens te bezoeken!

[1] Om dit artikel goed te kunnen volgen, is het het best om eerst het vorige artikel gelezen te hebben.

[2] Formeel is dit niet helemaal correct: de juiste definitie van ‘divergeren’ is dat de som niet convergeert – iets wat ook nog kan gebeuren als de losse termen wél steeds kleiner worden – maar in dit artikel kun je ervan uitgaan dat ook de individuele termen groter worden.

[3] We laten hier enkele natuurkundige constanten buiten beschouwing die in het argument dat volgt niet van belang zijn.

[4] De precieze reden hiervoor is zeer technisch van aard: de uitdrukking voor F zou je formeel gezien kunnen uitrekenen door middel van een zogeheten padintegraal met vaste randvoorwaarden. Het uitvoeren van die berekening blijkt onmogelijk te worden wanneer er geen stabiel vacuüm bestaat.