De padintegraal (3): Quantumstatistiek

De quantummechanica vertelt ons dat de natuur op de allerkleinste schaal lijdt onder een bepaalde statistische onzekerheid, die niet te wijten valt aan onze technische tekortkomingen. Dit beeld wordt bevestigd door de padintegraal die ik in de twee voorgaande artikelen in deze serie introduceerde. Hoe werkt de statistiek van de padintegraal nu precies?

Zoals eerder besproken in de serie artikelen over quantumfysica, is quantummechanica inherent niet-deterministisch: gegeven de begintoestand van een subatomair deeltje kunnen we nooit met zekerheid zeggen waar datzelfde deeltje zich een tijd later precies bevindt. Het enige wat we kunnen doen is de kans uitrekenen dat we het deeltje later op een zekere locatie zullen aantreffen. In het vorige artikel kon je lezen dat de quantummechanische padintegraal – oorspronkelijk geformuleerd door Richard Feynman – precies dit doet: door alle paden waarlangs een deeltje van A naar B kan gaan mee te nemen in de berekening, konden we deze kans bepalen.

In dit artikel wil ik de paralellen tussen kansrekening en quantummechanica nog iets meer uitlichten.  Aan de hand van enkele bekende voorbeelden uit de kansrekening zal ik enkele basisconcepten van de statistiek introduceren, en vervolgens beargumenteren dat de padintegraal diezelfde objecten ook kan berekenen.

Een dobbelsteenworp

We beginnen met een schoolvoorbeeld uit de kansrekening: een worp met een zeszijdige dobbelsteen. Stel je voor dat we de dobbelsteen één enkele keer mogen werpen, wat zijn dan de mogelijke uitkomsten? Dat zijn dan uiteraard de getallen één, twee, drie, vier, vijf en zes.  Al deze uitkomsten vormen samen een zogeheten discrete verzameling \( X \) (dat wil zeggen: geen continue verzameling zoals die van alle getallen tussen 1 en 2):

\( X = \{1, 2, 3, 4, 5, 6\} \).

Een dergelijke verzameling wordt in de statistiek ook wel de uitkomstruimte genoemd: het is de ‘ruimte’ die alle mogelijke uitkomsten bevat.

Aangezien een dobbelsteen symmetrisch is, kunnen we ervan uitgaan dat iedere uitkomst een gelijke kans heeft. Dat betekent in dit geval dat iedere uitkomst een kans van 1/6 heeft, aangezien de som van alle kansen één (oftewel: 100%) moet zijn – er moet per slot van rekening iets worden gegooid. Wiskundig gezien betekent dat dat

\( \sum_{x=1}^6 \frac{1}{6} = \frac{1}{6}+\frac{1}{6}+\frac{1}{6}+\frac{1}{6}+\frac{1}{6}+\frac{1}{6} = 1 \).

Alle kansen die we associëren met de gegeven uitkomsten in \( X \) kunnen we samenvatten in de zogenaamde kansverdeling \( P(x) \), een functie die aan iedere uitkomst \( x \) in de verzameling \( X \) een kans toewijst. In het geval van de enkele dobbelsteen is deze functie heel eenvoudig, namelijk \( P(x) = 1/6 \) voor elke mogelijke waarde van \( x \). De functie kan worden weergegeven in de volgende grafiek:

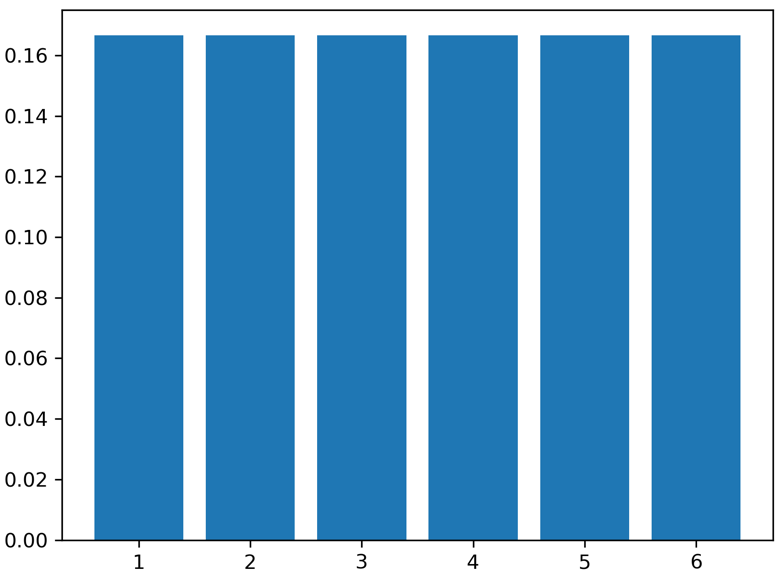
Een dergelijke kansverdeling staat bekend als een uniforme kansverdeling, aangezien alle uitkomsten exact dezelfde kans toegedicht krijgen.

Nu kunnen we vooraf nooit precies weten wat de uitkomst van één enkele dobbelsteenworp zal zijn, maar wel wat de verwachte uitkomst is. Om preciezer te zijn: als we heel vaak de dobbelsteen zouden gooien, wat verwachten we dan dat gemiddeld de uitkomst zal zijn? Dit is de verwachtingswaarde, die we noteren als \( \langle x \rangle \), en die we kunnen berekenen door iedere uitkomst te vermenigvuldigen met de kans op die uitkomst en vervolgens de resultaten bij elkaar op te tellen:

\(  \langle x \rangle = \sum_{x=1}^6  x P(x)  = \frac16 + \frac26 + \frac36 + \frac46 + \frac56 + \frac66 =3{,}5 \).

Gemiddeld verwachten we dus dat we 3,5 ogen gooien. Natuurlijk is het onmogelijk om met één dobbelsteen precies drie en een half oog te gooien, maar als we duizendmaal de dobbelsteen werpen, verwachten we zo’n 3500 ogen in totaal te gooien – of in elk geval iets dat relatief dicht in de buurt daarvan komt.

De verwachtingswaarde van \( x \) die we net hebben uitgerekend, wordt in de statistiek vaak aangeduid met de Griekse letter \( \mu \) (‘mu’) en noemen we ook wel het gemiddelde. Er zijn echter nog veel meer verwachtingswaarden die we kunnen uitrekenen. Om dit te zien generaliseren we de bovenstaande berekeningen naar de volgende:

\( \langle f(x) \rangle = \sum_{x=1}^6  f(x) P(x) \).

Deze vergelijking zegt dat we, wanneer we de verwachtingswaarde van een willekeurige functie \( f(x) \) willen uitrekenen, de functiewaarde voor elke \( x \) vermenigvuldigen met de bijbehorende kans \( P(x) \), en het resultaat sommeren over alle mogelijke uitkomsten in \( X \). Als je nog eens goed terugkijkt, dan zie je dat we hierboven al de verwachtingswaarden van de functies 1 en x hebben berekend: \(  \langle 1 \rangle = 1 \) en \( \langle x  \rangle = \mu \) . Niemand weerhoudt ons er echter van om ook andere functies te proberen.

Eén bijzonder interessant voorbeeld is de variantie: \( \sigma^2 = \langle (x-\mu)^2  \rangle \), die de mate van ‘spreiding’ van de uitkomsten aangeeft. Voor de dobbelsteenworp vinden we:

\( \sigma^2  = \frac{(1-3{,}5)^2+(2-3{,}5)^2+(3-3{,}5)^2+(4-3{,}5)^2+(5-3{,}5)^2+(6-3{,}5)^2}{6} = \frac{35}{12}\).

De wortel van de variantie, die bekend staat als de standaarddeviatie, is dan \( \sigma \simeq 1{,}71 \). De variantie vertelt ons grofweg hoe ver de verschillende uitkomsten gemiddeld uit elkaar liggen. Dat is ook de reden dat we de variantie \( \sigma^2 \) hebben genoemd: het is de wortel ervan, \( \sigma \) dus, die de meest voor de hand liggende betekenis heeft.

Laten we deze lessen nu meenemen naar het volgende voorbeeld, waar we geen discrete, maar een continue verzameling van uitkomsten treffen.

De normaalverdeling

De meeste meetuitkomsten die de natuur beschrijven zijn niet te bevatten in een discrete verzameling. Denk bijvoorbeeld aan de lengte van een mens, of  het gewicht van je huisdier. Zulke grootheden drukken we uit in getallen die een reeks decimalen dragen – in het geval van lengtes bijvoorbeeld niet alleen 182 cm of 183 cm, maar ook alle mogelijke lengtes daartussenin. Als we de lengte van honderd willekeurige mensen op straat zouden opmeten, dan verwachten we dat de mogelijke uitkomsten zich bevinden in een continue verzameling. In het geval van de lengtes van mensen verwachten we

\( X =(0, \infty) \).

Dat wil zeggen: alle positieve getallen. Heel grote waarden zoals 1732,4cm zullen in de praktijk natuurlijk niet voorkomen, maar we spelen op safe en stoppen dus direct maar álle positieve getallen in \( X \). Voor de uitkomsten van onze berekeningen maakt dat zoals je zult zien niets uit. Er zijn ook experimenten voor te stellen waar de uitkomstruimte echt een eindig interval \( (a, b) \) is, zoals het tijdstip waarop de eerste score in een basketbalwedstrijd wordt gemaakt.

Voor veel van deze experimenten blijkt er een universele kansverdeling te zijn die ze verbazingwekkend goed beschrijft: de normaalverdeling.

De normaalverdeling is een symmetrische kansverdeling die overal in de natuur opduikt en die bijvoorbeeld bij heel goede benadering van toepassing is op de lengtes van mensen¹. De normaalverdeling in zijn meest algemene vorm wordt omschreven door de functie

\( P(x)   = \frac{1}{\sigma \sqrt{2\pi}} e^{-\frac{1}{2\sigma^2} \left(x-\mu \right)^2}  \)

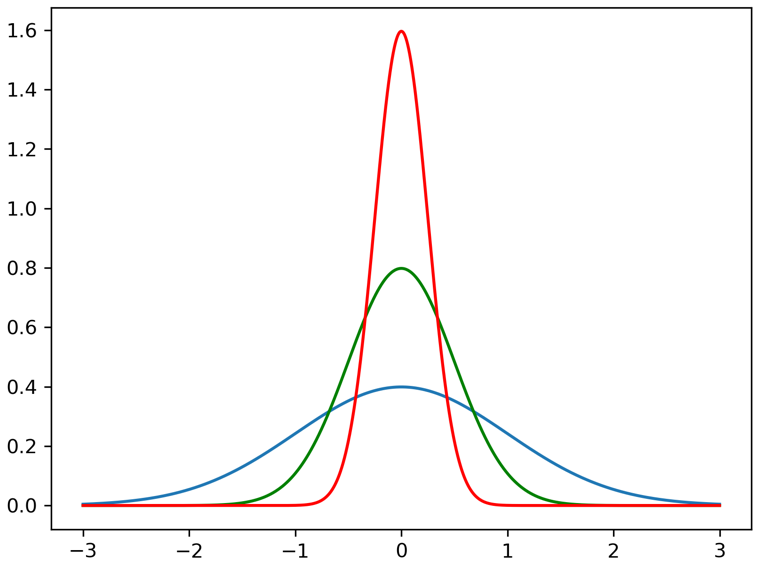
Deze verdeling kent twee parameters \( (\mu, \sigma) \) die je kunt kiezen zoals je wilt en die – zoals de symbolen doen vermoeden – het gemiddelde en de variantie van de verdeling bepalen. In afbeelding 3 hebben we drie van zulke normaalverdelingen afgebeeld, ieder met een andere waarde voor \( \sigma \). We zien dat wanneer \( x \) veel groter of veel kleiner dan \( \mu \) wordt, dat de kansdichtheid nagenoeg nul wordt. Uitkomsten die dus ver weg van het gemiddelde liggen (waarbij wat ‘ver weg’ is wordt bepaald door de gekozen waarde van \( \sigma \)), krijgen een veel kleinere kans toegewezen.

Bij de dobbelsteenworp zagen we dat de som van alle kansen één moest zijn. Hier geldt dezelfde voorwaarde: alle kansen bij elkaar opgeteld moeten één geven. Maar omdat we hier met een continue verzameling van uitkomsten werken, nemen we niet de som van alle kansen, maar integreren we over alle kansen. Om preciezer te zijn, in dit geval heeft de kansverdeling de interpretatie van een kansdichtheid: in het voorbeeld van de lengtes bijvoorbeeld de ‘kans per centimeter’. Het equivalent van ‘alle kansen optellen’ is in dit geval het integreren van de kansdichtheid over het interval \( X = ( a , b) \). Uitgaande van het simpele geval dat \( X = (-\infty , +\infty ) \), toont ook voor de normaalverdeling een ietwat technische berekening – die de lezer niet hoeft te reproduceren – aan dat

\( \int_{-\infty} ^ \infty \  P(x) \ dx = 1 \).

Vervolgens kunnen we ook weer de verwachtingswaarden van \( x \) en \( (x-\mu)^2 \) kunnen uitrekenen. Twee wederom wat technische berekeningen leiden dan tot \( \langle x  \rangle = \mu \) en \( \langle (x-\mu)^2  \rangle = \sigma^2  \), wat natuurlijk precies de twee parameters zijn die om die reden in de definitie van de normaalverdeling zo genoemd zijn.

Quantummechanica 

Nu maken we de stap naar quantummechanica, waar het hele verhaal nog net één stapje complexer wordt. Zoals in ieder statistisch model kun je ook in de quantummechanica onmogelijk de toekomstige waarde van een grootheid voorspellen, maar slechts de verwachtingswaarde ervan berekenen. In het geval van quantummechanica is allereerst de vraag: wat is de uitkomstruimte en de bijbehorende kansverdeling?

In de generieke situatie waarin een deeltje van A naar B beweegt, zagen we in het vorige artikel dat we in de padintegraal rekening moeten houden met alle paden die van A naar B lopen. De verzameling van al deze mogelijke paden blijkt onze uitkomstruimte te zijn:

\( X = \text{ alle mogelijke paden van A naar B} \).

Net zoals bij de dobbelsteenworp en de normaalverdeling, moeten we vervolgens ook een kans(dichtheid) \( P[x(t)] \) toewijzen² aan ieder pad \( x(t) \). Dit is het ‘gewicht’ dat we in het vorige artikel hebben besproken:

\( P[x(t)] = e^{iS[x(t)]/\hbar} \).

Hier is de functie \( S[x(t)] \) de ‘actie’ die we uitlichtten in het eerste artikel van deze reeks en \( \hbar \) de gereduceerde constante van Planck.

Dan vinden we, gegeven een functie \( f[x(t)] \) die afhangt van het pad \( x \), de verwachtingswaarde³

\( \langle f[x(t)] \rangle = \int_{x(0) = A}^{x(t’) = B}  f[x(t)] \, e^{i S[x(t)] /\hbar}  dx \).

De functie \( f[x(t)] \) kan nu van alles zijn: de plaats halverwege het tijdsinterval, de snelheid van het deeltje op een bepaald moment, de kinetische energie die het deeltje wint of verliest, noem maar op. Wederom houden we rekening met alle paden die op punt A beginnen en op punt B eindigen in het tijdbestek \( [0, t’]\). Het moet gezegd worden dat deze berekening in de praktijk buitengewoon ingewikkeld is, en zeker niet zo makkelijk als in de twee voorgaande voorbeelden van de dobbelsteen en de normaalverdeling. Er zijn echter allerlei trucs die we kunnen toepassen om zulke verwachtingswaarden te berekenen.

Hoewel de uitkomstruimte in elk van de modellen anders is, is het onderliggende idee hetzelfde: we hebben een verzameling uitkomsten \( X \) met ieder een kans(dichtheid) \( P(x) \). Gegeven een functie \( f(x) \) die afhangt van de uitkomst \( x \), berekenen we de verwachtingswaarde \( \langle f(x) \rangle \) door alle uitkomsten te vermenigvuldigen met hun kans(dichtheid) en het resultaat vervolgens te sommeren of te integreren. Technisch gezien is er een reeks van verschillen natuurlijk, maar in principe zien we hetzelfde onderliggende idee bij alle drie de voorbeelden.

Als afsluiting wil ik nog de volgende interessante observatie maken: als we de kansverdeling \( P(x) \) van de normaalverdeling nog eens beter bestuderen, dan valt het volgende op. In de exponent staat de uitdrukking \( –(x-\mu)^2 \). Die uitdrukking beschrijft een parabool met een extreme waarde – ook wel ‘stationair punt’ genoemd – op \( x = \mu \). We zien in afbeelding 3 dat, wanneer de variantie \( \sigma^2 \) heel klein wordt, de kansverdeling zich centreert rondom dit stationaire punt \( x= \mu \). In de limiet \( \sigma^2 \to 0 \) wordt de piek rondom \( x = \mu \) zo nauw dat alleen een uitkomst héél dicht in de buurt van \( x=\mu \) nog een realistische uitkomst is van de normaalverdeling

Dit is precies wat we in het vorige artikel voor de padintegraal verstonden onder de ‘klassieke limiet’! Daar zagen we dat de actie \( S[x(t)] \) een stationair punt[4] had dat als enige nog een bijdrage leverde aan de padintegraal wanneer \( \hbar  \) heel klein was ten opzichte van andere grootheden in het experiment. Als we de kansverdelingen van de normaalverdeling en de quantummechanica vergelijken, zien we dezelfde structuur: bij de normaal verdeling delen we \( –(x-\mu)^2 \) door de variantie, terwijl we in de padintegraal de actie delen door de gereduceerde Planck-constante. Omgekeerd kunnen we de gereduceerde Planck-constante dus ook opvatten als een parameter die de variantie van de padintegraal bepaalt.

Al met al kunnen we concluderen dat de padintegraal ons in staat stelt om de statistiek die aan de quantummechanica ten grondslag ligt beter te begrijpen; iets wat duidelijk wordt als we de padintegraal vergelijken met simpelere voorbeelden uit de bekende kansrekenening. In de gewone statistiek bestaat de uitkomstruimte uit een verzameling getallen – discreet of continu – en in de quantummechanica uit mogelijke paden. Als we nog een stap verder gaan komen we uit bij de quantumveldentheorie: hier bestaat de uitkomstruimte uit alle mogelijke ‘veldconfiguraties’ en ook daar kunnen we een padintegraal uitschrijven om berekeningen uit te voeren. Dit onderwerp laat ik echter nog even rusten voor een andere keer!

[1] Eén kleine subtiliteit: de normaalverdeling gaat ervan uit dat uitkomsten overal op de getallenlijn kunnen liggen, tussen min oneindig en plus oneindig. De lengtes van mensen kunnen – zoals eerder gezegd – niet negatief zijn, en ook niet extreem groot, en dus is de normaalverdeling niet helemaal juist. De standaarddeviatie van de ‘best passende’ normaalverdeling is in dit geval echter zo klein dat volgens die verdeling de kans op het vinden van iemand met een negatieve lengte verwaarloosbaar klein is, zelfs als je alle 8 miljard inwoners op aarde zou meten. De normaalverdeling komt dus nog altijd extreem goed overeen met de echte verdeling die we in de wereld om ons heen aantreffen.

[2] We gebruiken hier blokhaken omdat \( P[x(t)] \) een ‘functionaal’ is: in plaats van een getal als input neemt de functionaal een functie – namelijk \( x(t) \) –  als input.

[3] Hier laten een we stiekem een voorfactor weg die de hele padintegraal normaliseert, i.e. garandeert dat \( \langle \, 1 \, \rangle = 1 \). Deze voorfactor is echter niets anders dan een getal, dus dit verandert niets wezenlijks aan de kansrekening die hier plaatsvindt.

[4] Dit stationaire punt van \( S[x(t)] \) noemden we in het eerste artikel van deze reeks het ‘pad van minimale actie’.