De padintegraal (2): van klassiek naar quantum

In het eerste artikel uit deze serie over de padintegraal schreef ik hoe het gedrag van objecten in de klassieke mechanica, die de natuurkunde op onze grote schaal beschrijft, verklaard kan worden aan de hand van het ‘principe van minimale actie’. In dit principe is er de actie \( S[x(t)] \) die ons, gegeven een pad \( x(t) \) dat een deeltje van A naar B aflegt, een getal \( S \) geeft. Het pad waarvan de actie \( S[x(t)] \) minimaal is, is het pad dat het deeltje daadwerkelijk aflegt. In onze grootschalige ‘klassieke’ wereld eindigt het verhaal daar, maar hoe werkt dit op de subatomaire schaal waar de wetten van de quantummechanica gelden?

Klassieke mechanica is deterministisch: gegeven de locatie en snelheid van een deeltje op een initieel tijdstip, kunnen we voorspellen waar het deeltje zich op een later tijdstip bevindt, en welke snelheid het dan heeft. In de quantummechanica geldt dat niet. We kunnen daar slechts spreken van de kans dat je het deeltje op een later tijdstip op een gegeven locatie kunt terugvinden. Quantummechanica is daarom niet deterministisch.

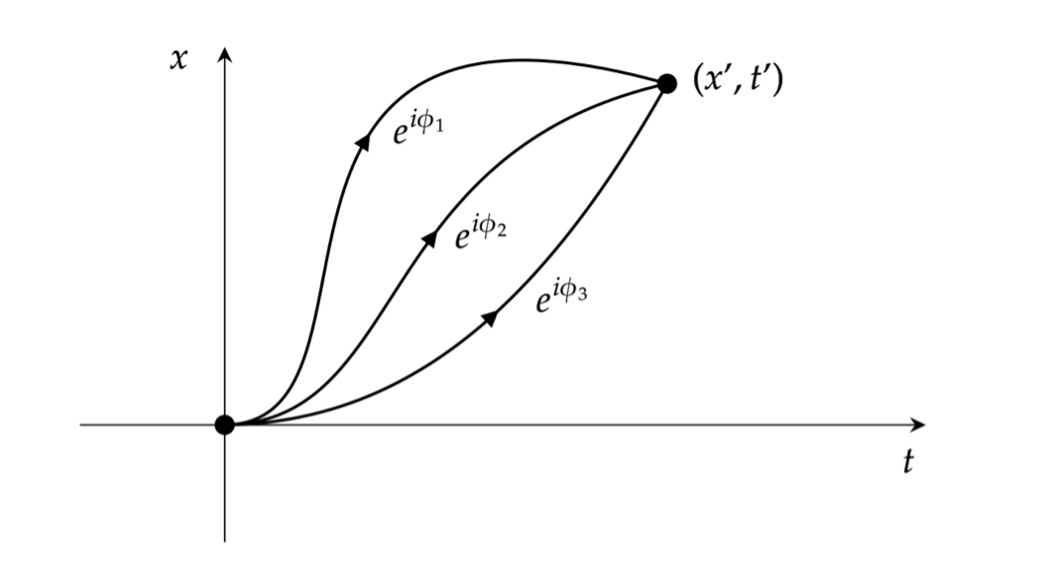
Als alles draait om kansen, is de vraag natuurlijk hoe je zo’n kans dan kunt uitrekenen. De bekende natuurkundige Richard Feynman kwam met een interessante oplossing voor dit vraagstuk. Stel dat een deeltje zich initieel bevindt op een punt dat we P noemen, met ruimtetijd-coördinaten \( (x, t) = (0,0) \). Vervolgens willen we weten wat de kans is dat we ditzelfde deeltje terugvinden op ruimtetijd-coördinaten \( (x, t) = (x’, t’) \), een punt dat we Q noemen. Volgens Feynman wordt de kans die we zoeken dan bepaald door alle mogelijke paden die dit deeltje tussen P en Q kan afleggen.

Hier komt dan eindelijk de hoofdrolspeler van deze serie om de hoek kijken: wiskundig gezien wordt deze kans berekend door een zogenoemde padintegraal. Deze padintegraal is een som die loopt over alle mogelijke paden van P naar Q. Aan al deze paden wordt een ‘gewicht’  toegewezen, wat we schrijven als \( e^{i\phi} \): een complex getal dat verschilt per pad.  Door al deze complexe getallen bij elkaar op te tellen – één voor ieder mogelijk pad – krijgen we een nieuw complex getal dat we de amplitude \( A \) noemen:

\( A =  \sum_{\text{alle paden van P naar Q}} e^{i \phi}\).

Deze amplitude hangt af van de eindlocatie \( x’ \) die we kiezen, en daarom schrijven we ook vaak \( A =  A(x’) \) . De kans¹ dat we uiteindelijk ons deeltje terugvinden op eindpunt \( x’ \) wordt dan gegeven door het kwadraat van de absolute waarde van de amplitude:

\( \text{kans deeltje te vinden op }x’ = |A(x’)|^2 \).

Als je eerder kennis gemaakt hebt met complexe getallen, dan zul je je misschien herinneren dat de absolute waarde van een complex getal altijd reëel en positief is, en het kwadraat ervan is dat dus ook. Dit is precies wat we vragen van een getal dat een kans moet beschrijven.

Het tweespletenexperiment

Waarom moeten we voor het berekenen van de kans om een deeltje ergens aan te treffen, rekening houden met alle mogelijke paden naar die locatie? Is er niet simpelweg één ‘correct’ pad, zoals in het geval van de klassieke mechanica? Om deze vraag te beantwoorden gaan we terug naar het beroemde tweespletenexperiment – beschreven in een eerder artikel door Marcel Vonk – waarmee je kunt laten zien dat subatomaire deeltjes zoals bijvoorbeeld elektronen zich als deeltjes én golven kunnen gedragen. In dit experiment worden elektronen één voor één afgevuurd op een detector waarvoor een schot met twee spleten staat gepositioneerd – zie de linker tekening in afbeelding 2. De detector meet dan precies op welke locatie \( x’ \) het elektron op de detectorplaat landt. Klassiek gezien zou je denken dat alle elektronen eindigen op één van twee mogelijke locaties op de detectorplaat, recht achter de twee spleten in het schot. Wat echter in het artikel over het tweespletenexperiment werd uitgelegd, is dat zich in plaats daarvan een interferentiepatroon aftekent op de plaat. Dit is een indicatie dat de elektronen, die één voor één afgeschoten zijn, zich als golven gedragen die door beide spleten tegelijkertijd zijn gegaan!

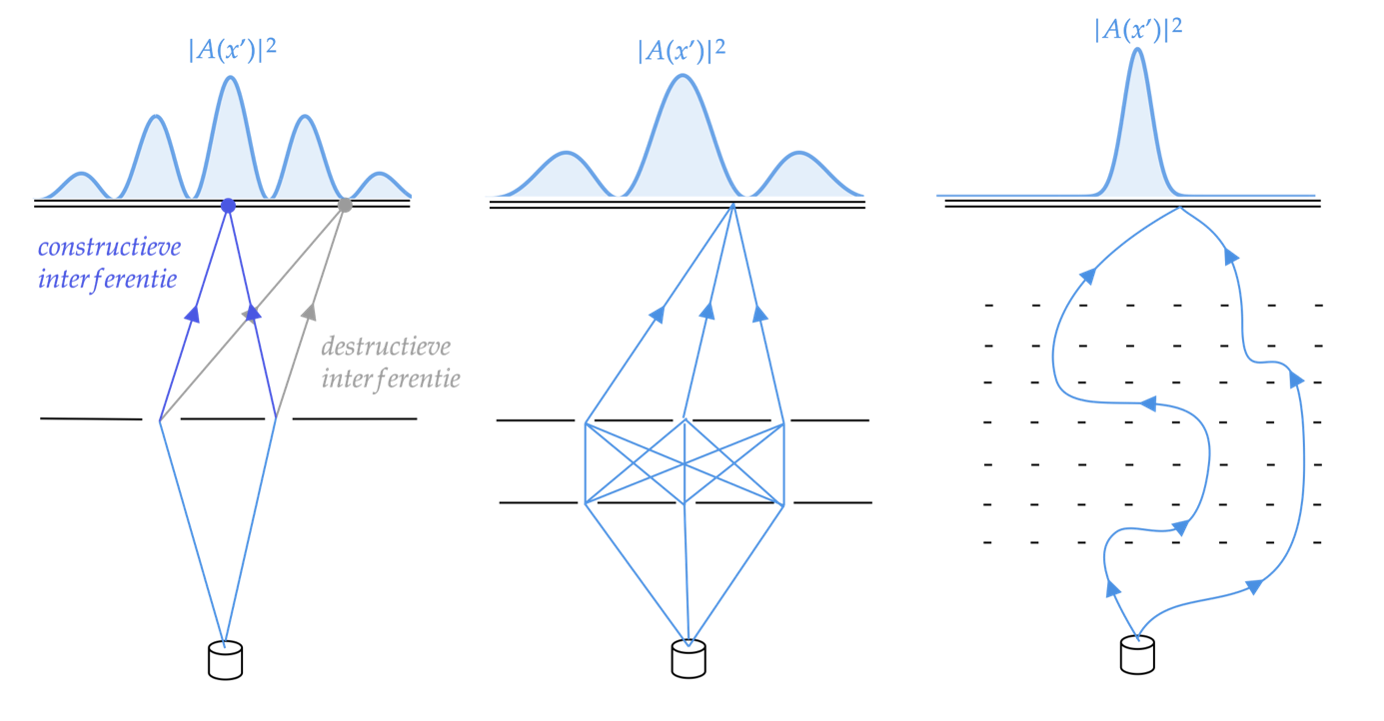
Het interessante aan het interferentiepatroon in het tweespletenexperiment is dat we het ook kunnen interpreteren als de kans dat een elektron eindigt op een gegeven punt op de detectorplaat. In afbeelding 2 aan de linkerzijde zien we bijvoorbeeld paden naar twee verschillende eindpunten waar de kans om te eindigen nul en niet nul kan zijn. De uiteindelijke waarde van de amplitude op een gegeven eindpunt \( x’ \) wordt bepaald door de interferentie van de golven die langs de twee mogelijke paden naar datzelfde eindpunt zijn gegaan. Als je de elektronen als golven beschouwt kun je niet alleen de interferentie verklaren, maar ook de bijbehorende amplitudes \( A(x’) \) uitrekenen²:

\( A(x’) = e^{i\phi_1}+e^{i\phi_2} \)

Als deze twee contributies precies tegen elkaar wegvallen, is er spraken van destructieve interferentie (\( A(x’) = 0 \)), en als de twee contributies juist dezelfde fase hebben \( \phi_1 = \phi_2 \) dan is er sprake van constructieve interferentie.

Wat als we nu een derde spleet maken in het schot, en ook nog een extra schot erbij plaatsen? In dat geval – zie het midden van afbeelding 2 – verandert de amplitude voor ieder eindpunt \( x’ \), aangezien de mogelijke paden die het elektron kan nemen veranderen, en daarmee ook de mogelijke manieren waarop het elektron met zichzelf kan interfereren. We kunnen dit idee opschalen tot extreme vormen: stel je voor dat er nog heel veel meer schotten tussen het startpunt en de detector staan, en dat deze schotten bijna oneindig veel spleten bevatten (rechterzijde afbeelding 2) dan vinden we een gigantisch grote hoeveelheid paden die het elektron kan afleggen en moeten we volgens de bovenstaande logica met ieder van deze paden rekening houden. In de limiet waarin we oneindig veel schotten hebben met oneindig veel spleten kan het deeltje praktisch ieder gekromd pad nemen dat je met pen en papier kunt tekenen. Een wiskundige consequentie hiervan is dat we de som over paden moeten vervangen door een integraal over paden, en dat is het object dat de padintegraal wordt genoemd:

\( A = \int_{x(0) = 0}^{x(t’) = x’} Dx e^{i \phi[x(t)]} \)

Om aan te geven dat we integreren over paden, niet zoals gebruikelijk over getallen, gebruiken de notatie \( Dx \) in plaats van \( dx \). De paden waarover we hier integreren moeten slechts voldoen aan twee randvoorwaarden: dat ieder pad begint op punt P (d.w.z. \( x(0) = 0 \)) en eindigt in punt Q (d.w.z. \( x(t’)= x’\)).

Dit is precies wat Feynman ons vertelde: de kans om een deeltje terug te vinden op een gegeven locatie wordt bepaald door alle mogelijk paden die het deeltje daarheen kan afleggen. De experimentele resultaten van het beroemde tweespleten-experiment, in combinatie met de denkbeeldig extensie hiervan naar oneindig veel schotten met oneindig veel spleten, leiden op een natuurlijke wijze tot Feynmans inzicht. De vraag rest ons dan alleen nog wat precies het gewicht \( e^{i \phi[x(t)]}  \) is, en hoe we het uitrekenen.

Terugkeer van de actie en de klassieke limiet

Laat ik hier maar direct met de deur in huis vallen: de mysterieuze functie \( \phi\) die bepaalt welk complex getal we toewijzen aan een pad, blijkt precies de actie \( S \) te zijn die ik in het vorige artikel besprak! Om precies te zijn: de padintegraal blijkt als je die uitschrijft de volgende vorm aan te nemen:

\( A(x’) = \int_{x(0) = 0}^{x(t’) = x’} D[x(t)] e^{i S[x(t)] /\hbar} \).

In deze formule is \( \hbar \) de gereduceerde constante van Planck: de universele constante die ons vertelt op welke schaal de wetten van de quantummechanica relevant worden. Wat de padintegraal ons vertelt, is dat ieder pad – dat voldoet aan de eerder genoemde randvoorwaarden – een actie heeft, die leidt tot een complex getal \( e^{i S /\hbar} \). Als we al deze complexe getallen voor ieder pad ‘optellen’, vinden we de amplitude \( A(x’) \) die ons in staat stelt de kans te berekenen dat een deeltje op het punt Q eindigt.

Één van de prachtige eigenschappen van de padintegraal is dat we de regels van de klassieke mechanica er weer uit kunnen terugvinden. Zoals eerder gezegd bepaalt de Planck-constante \( \hbar \) op welke schaal quantumeffecten relevant zijn en wanneer niet. Omdat de constante van Planck in onze alledaagse eenheden gemeten zo’n ongelofelijk klein getal is (\( 1,054 * 10^{-34} \) Joule maal seconde) is de quantumschaal voor ons heel klein en zijn quantumeffecten moeilijk waar te nemen.  Om dit te begrijpen zullen we in een gedachte-experiment aannemen dat \( \hbar \) een parameter is die we zelf naar believen kunnen aanpassen. Welke paden leveren dan significante bijdragen aan de padintegraal, en welke niet?

Het gewicht \( e^{iS/\hbar} \) zal voor ieder pad een complex getal zijn dat op de eenheidscirkel ligt in het complex vlak, en dus absolute waarde (lengte) één heeft. Laten we een willekeurig pad bekijken, en naast dit pad nog twee extra nagenoeg identieke paden bestuderen – zie de linker figuur in afbeelding 3 in het rood. Voor ieder van deze paden kunnen we de actie uitrekenen, wat leidt tot drie verschillende gewichten \( e^{iS_{1}/\hbar} , e^{iS_{2}/\hbar} \) en \( e^{iS_{3}/\hbar} \). Aangezien \( \hbar \) heel klein is, is de factor \( 1/\hbar \) in de gewichten heel groot, en zorgen de verschillen tussen de acties \( S_1, S_2 \) en \(  S_3 \) dus voor drie compleet verschillende gewichten die – zoals in het midden van afbeelding 3 te zien – min of meer tegen elkaar wegvallen als we ze optellen. Dit is dezelfde destructieve interferentie die we in het tweespletenexperiment zagen: generieke paden zullen een bijdrage leveren aan de padintegraal die wordt tenietgedaan door de bijdragen van naburige paden. De meeste paden zullen dus een beperkte contributie leveren aan de padintegraal.

Er zijn echter ook paden waar deze destructieve interferentie niet plaatsvindt. Dit zijn de paden die voldoen aan ons principe van minimale actie! Laten we zo’n ‘minimaal’ pad en zijn naburige paden eens onder de loep nemen – in het groen in afbeelding 3. Wederom vinden we drie verschillende acties en daarmee drie verschillende gewichten. We zien nu echter dat de drie verschillende acties nagenoeg identiek zijn – \( S_4 \simeq S_5 \simeq S_6 \). Dit komt omdat we een ‘stationair’ punt bestuderen waar de ‘eerste afgeleide’ van de actie nul is.  Als we het pad dus alleen maar licht variëren, verandert de actie nagenoeg niet. Als gevolg hiervan zien we dat de drie gewichten elkaar niet tegenwerken, maar vrijwel ‘dezelfde kant op wijzen’ – zie rechterzijde van afbeelding 3. Hier is sprake van constructieve interferentie en deze paden bevatten dus wel relevante bijdragen aan de padintegraal!

Wat we zien is dat de paden die de actie minimaliseren³ (of dat bijna doen) de meest relevante bijdragen leveren aan de padintegraal. Het interessante is dat naarmate we de ‘quantumschaal’ \( \hbar \) in onze berekening kleiner maken, dit contrast alleen maar sterker wordt: kleine variaties in de actie \( S \) worden door de factor \( \frac{1}{\hbar} \) opgeblazen, wat leidt tot destructieve interferentie. De enige paden die hieraan ontkomen zijn de paden die zo dicht mogelijk bij een ‘minimaal pad’ liggen. In de limiet dat \( \hbar \) echt nul wordt, tellen alleen nog maar de paden mee die daadwerkelijk de actie minimaliseren. In het vorige artikel zagen we dat dit precies de paden zijn die deeltjes afleggen in de klassieke mechanica, en dus spreken we van de klassieke limiet.

Omdat de gereduceerde Planck-constante zo klein is merken we in ons alledaagse leven niets van de padintegraal: macroscopische objecten zoals tennisballen lijken altijd het pad van de minimale actie te volgen, zoals de klassieke mechanica voorspelt. Andere ‘quantumpaden’ worden door de bovengenoemde destructieve interferentie irrelevant en zijn praktisch onmeetbaar. Alleen als we experimenten doen op de subatomaire schaal, waar \( \hbar \) relatief gezien niet langer klein is, zien we dat deze andere paden ook relevant worden en een wezenlijke bijdrage leveren aan de padintegraal.

Samenvattend: we hebben gezien dat het concept van een ‘actie’ die natuurkundigen in de klassieke mechanica gebruiken, terugkeert in de quantummechanica. Of misschien is het wel beter om het andersom te zeggen: de padintegraal in de quantummechanica zorgt dat we in de grootschalige klassieke mechanica alleen de actie nodig hebben. Pas als we het gedrag van subatomaire deeltjes willen beschrijven moeten we niet meer alleen rekening houden met het pad van minimale actie, maar met alle mogelijke paden. De gereduceerde constante van Planck bepaalt op welke schaal deze andere paden relevant zijn, en wanneer niet.

Een ander interessant aspect van de padintegraal heb ik nog niet beschreven: het feit dat het formalisme van de padintegraal een statistische interpretatie van quantummechanica levert, en het rekenen met padintegralen dus in veel opzichten overeenkomsten met statistiek vertoont. Wat dat precies betekent voor de quantumwereld zal ik in een volgend artikel verder bespreken!

[1] Strikt genomen zijn er oneindig veel mogelijke eindpunten x’, en zou de kans om een deeltje precies op x’ aan te treffen dus 0 zijn. Wat de padintegraal eigenlijk uitrekent is de kansdichtheid: de kans ‘per kubieke meter’ om het deeltje in de buurt van x’ aan te treffen.

[2] Strikt genomen is deze berekening een benadering, en zouden we, zoals we verderop in het artikel zien, ook allerlei ‘kromme’ paden die door de twee spleten gaan moeten meerekenen. We blijken zulke effecten voor een klein aantal spleten echter bij heel goede benadering te kunnen verwaarlozen.

[3] Technisch gesproken geldt precies hetzelfde als de paden de actie maximaliseren; in wiskundige termen gaat het erom dat de actie een extremum heeft. In de praktijk zullen in veel gevallen de minima wel bijdragen aan de padintegraal geven die nog veel groter zijn dan de bijdragen van maxima of zadelpunten.